Notation
-
u 8 Friction velocity (m s−1)
-
u *r Real friction velocity, corresponding to the friction velocity modified by the presence of snow particles (m s −1)
-
u *t Threshold friction velocity (m s −1)
-
U F Particle-settling velocity (m s −1)
-
(ū,
 ) Mean velocity components in the x (m) (horizontal) and y (m) (vertical) directions (m s −1)
) Mean velocity components in the x (m) (horizontal) and y (m) (vertical) directions (m s −1) -
u i Mean velocity component in the Ox i direction (m s −1)
-
z 0 Aerodynamic roughness heigh (m)
-
D p Particle diameter (m)
-
V p Particle volume (m3)
-
σs Turbulent Schmidt number
-
ρ Air density (kg m−3)
-
ς Particle density (kg m −3)
-
γ Bulk density of the snow (kg m −3)
-
g Gravitational acceleration (m s −2)
-
K Von Kármán's constant
-
h Surface level (m)
-
t Time (s)
-
p Pressure (N m −2)
-
 Particle concentration (kg m −3)
Particle concentration (kg m −3) -
C s Particle concentration in the saltation layer (kg m −3)
-
C max Maximum particle concentration in the saltation layer (kgm −3)
-
υ t Turbulent viscosity coefficient (m s −1)
-
φ g Erosion or deposition flux (kg m−2 s −1)
-
φ g Mass flux between the suspension and the saltation layers (kg m −2 s−1)
-
Q s Total mass-transport rate per unit of lateral dimension in the saltation layer (kg m−1 s−1)
-
Q t Total mass-transport rate per unit of lateral dimension in the suspension layer (kg m−1 s−1)
-
h s Height of the saltation layer (m)
-
k Turbulent kinetic energy (m2 s-2)
-
ϵ Dissipation of the turbulent kinetic energy (m2 s−3)
Introduction
In high mountain areas, blowing snow produces cornices creating dangerous avalanche-starting zones. In other areas, blowing snow reduces visibility and creates snow-drifts. Drifting snow poses economic problems, especially for roads and railways. Taking snowdrift formation into account is therefore a necessity both in terms of predicting and controlling drift patterns. However, it is time-consuming and often unrealistic to study full-scale snowdrifts in the field. Physical modelling, carried out in wind-tunnels since the 1930s, allows one to study the formation of small-scale snowdrifts but raises a difficult problem: all similitude requirements cannot be satisfied simultaneously. Therefore, we have in recent years turned to numerical modelling. As an introduction, we give a brief, non-exhaustive review of computer modelling of aeolian transport before introducing our own approach.
The Existing Numerical Models
Two categories of multiphase How theories can be used for modelling drifting snow: the Eulerian multiphase How model and the Lagrangian particle model. The Eulerian multiphase flow model can be simplified by treating the particles as a continuum field and by using a convection–diffusion equation for particle concentration. We present later an example of each type of model.
Drifting-Snow Models of Reference Uematsu, Kaneda, Takeuchi, Nakata and YukumiUematsu and Others (1989) and Reference Liston, Brown and DentListon and Others (1993,Reference Liston, Brown and Dent1994)
This kind of model was first developed by Reference Uematsu, Kaneda, Takeuchi, Nakata and YukumiUematsu and others (1989) and followed by Reference Liston, Brown and DentListon and others (1993). It is based on two-dimensional time-averaged Navier–Stokes equations and a modified k–ϵ turbulence model proposed by Reference Chen and WoodChen and Wood (1985). These equations allow one to obtain the turbulent-flow field, the turbulent kinetic energy and the kinetic-energy dissipation.
Concerning snow transport, Reference Liston, Brown and DentListon and others (1993) took the saltation process into account and treated snow-drifting using the following total mass-transport rate per unit of lateral dimension:

where C is a constant.
Afterwards, Reference Liston, Brown and DentListon and others (1994) introduced the diffusion process using the particle mass-concentration equation which takes the following form in the turbulent-diffusion layer:

The concentration at the bottom of the suspension layer is the mean concentration in the saltation layer. Changes in the snow-surface level are described by the vertically integrated mass-continuity equation:

Snow deposition is computed assuming that snow accumulates where shear velocity falls below the threshold shear velocity. The control volumes are filled one by one. When a control volume is filled with snow, the flow field (which depends on the surface topography) is recomputed and the same process is repeated until the accumulated snowdrift reaches an equilibrium profile. Reference Liston, Brown and DentListon and others (1994) considered implicitly that the mass-transport rate Q s reacts instantaneously to a change in friction velocity (Equation (1)). So, this numerical model does not take the inertia of snow erosion and snow deposition into account. In fact, drift-particle saturation is not reached immediately when the wind-friction speed increases, and deposition occurs progressively when the wind-friction speed decreases.
If this model makes it possible to compute snowdrifting at equilibrium, it does not estimate the time required to obtain a given snow accumulation and variations in snowdrift formation. For example, the windward and leeward drift generated by a solid fence are forming simultaneously. This result is opposite to the results obtained by the numerical simulation of Reference Liston, Brown and DentListon and others (1994).
Drifting-Sand Model of Reference Anderson and HaffAnderson and Haff (1991)
Unlike the previous model, the inertia of sand erosion and sand deposition is taken into account in the model proposed by Reference Anderson and HaffAnderson and Half (1991). This numerical model, developed for the reptation and the saltation in a turbulent boundary layer over a flat area, is based on the “splash” function. The “splash” function, generated from physical and numerical experiments, allows one to formulate statistically grain–bed interaction: the “splash” function returns the number of ejected particles, the probability distribution of their ejection velocities and the velocities of the rebounding grains.
Encouraging results are obtained using the “splash” function for sand drift (Reference Chen and WoodAnderson and Haff, 1991). However, this model is not suitable for snow and turbulent separated flows over obstructions without modification.
First, it is necessary to introduce suspension. But Reference Anderson and HaffAnderson and Haff (1991) considered that it is possible to use the continuum theory far from the bed. In addition, this model cannot be applied in the case of a turbulent separated flow over obstructions: the estimations of “grain stress” and trajectory times are no longer valid. Lastly, it has appeared that the “splash” function defined for sand particles differs from that defined for snow particles because of the shape and the cohesion of the snow particles (Reference Naaim-BouvetNaaim-Bouvet, 1997).
Numerical Simulation of Snowdrifting
Although the numerical model proposed by Anderson and Haff is physically more sound, it is currently difficult to adapt it to snow particles because of the lack of knowledge about the “splash” function. In the present state of our knowledge, we do not have any idea of the form taken by t he “splash” function for different types of snow. We therefore propose a numerical simulation based on the continuum theory and taking into account inertia of snow erosion and snow deposition by means of erosion and deposition fluxes. We also use the modified κ–ϵ model proposed by Reference Chen and WoodChen and Wood (1985) to close this system of equations.
Governing Equations
The model is based on the mass-conservation laws for both the fluid and the particles, the conservation of momentum for the mixture (air + particles), and the modified κ–ϵ model.
Air-mass conservation is

Particle-mass conservation in suspension layer is

Particle-mass conservation in the saltation layer is

Momentum conservation is

Turbulent kinetic energy conservation is

Turbulent kinetic-energy dissipation conservation is

where

φ
s is the mass flux exchanged between the suspension and the saltation layer. It is determined by the difference between the diffusion flux proportional to ![]() and the settling flux which is proportional to U
F
C.
and the settling flux which is proportional to U
F
C.
φ g is the mass flux exchanged between the flow and the ground, determined by using the erosion or deposition flux. If h, the snow depth, is non-zero, and if the friction velocity u * at ground level is greater than the threshold friction velocity u * t, then φ g is equal to the erosion flux. If the friction velocity u * at ground level is lower than the threshold friction velocity u * t, then φ g is equal to the deposition flux. If the friction velocity u * at ground level is equal to the threshold friction velocity u * t, then φ g is equal to zero.
Changes in snow-surface level are described by the following equation:

Numerical Resolution
The complete system is solved by a Godunov numerical scheme of second-order accuracy in space and time. The resolution is obtained from a finite-element mesh. In this way, it is possible to adapt the mesh to the temporal changes of the drift. Changes in snow depth are slow. In contrast, turbulent-flow field variation is fast. Therefore, the following computation process is used: we compute the flow field until a stationary solution is reached; this velocity field allows us to compute variations in snow depth until a significant variation is observed in the deposit height. In our simulations, we consider a variation of 2 mm is significant (in the case of fence height = 4 cm). Then the flow field is recomputed and the process is repeated along the formation of the drift.
Boundary Conditions
Momentum and Turbulence
The model needs a set of boundary conditions near the ground where the flow is considered to be a turbulent boundary layer defined by friction velocity and roughness. The turbulence parameters near the ground are linked to u * by:


where: σκ = 1, σϵ = 1.3, cϵ1, = 1.44, cϵ2 = 1.92.
Erosion Flux
First, we make the assumption that snow particles with cohesion are mainly entrained by direct aerodynamic forces. This simplification is not applicable to all cases: for example, reptation has considerable importance when cold loose snow is blown (Reference Naaim-BouvetNaaim-Bouvet, 1997). The number N
a of entrained grains per bed area unit per time unit is proportional to the excess shear stress (Reference Anderson and HaffAnderson and Haff, 1991) : 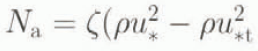 where ζ is a constant N
−1
s−1).
where ζ is a constant N
−1
s−1).
The erosion flux φe area unit may be written
The coefficient A varies with the degree of intergranular bonding in the surface layer. The velocity profile is modified by snow transport but we have few experimental data on changes in shear velocity at the bed as a function of particle concentration. Numerical results obtained by Reference Anderson and HaffAnderson and Haff (1991) and Reference McEwan and WillettsMcEwan and Willetts (1991) are conflicting. Reference Anderson and HaffAnderson and Haff (1991) predicted that at steady state the shear stress at the bed had fallen slightly below the threshold shear stress for aerodynamic entrainment. Reference McEwan and WillettsMcEwan and Willetts (1991) predicted that at steady state the shear stress at the bed is roughly equal to its initial value. Reference KindKind (1975) assumed that the shear stress at steady State must remain at the threshold value in order to maintain the bed “mobile”. We retain Kind's assumption. At first, we suggest that the friction velocity is modified. The real friction velocity near the ground u*r, which is responsible for erosion, is linked to the friction velocity by the following formula

When the particle concentration is zero, the “real” friction velocity is equal to the friction velocity. When the particle concentralion reaches its highest value (steady state), the “real” friction velocity is equal to the threshold-friction velocity.
The erosion flux (Equation (14)) becomes

For snow particles, only the experimental data from Reference TakeuchiTakeuchi (1980) are available. We chose to reproduce one of his experimenls numerically in order to validate the erosion model. We considered the one referenced No. 3, because in this case snowfall was limited. The snowdrifting flux reached saturation about 250 m downwind of the starting point. The saturated horizontal snow-mass flux, measured up to 30 cm above the snow surface, was approximately 20 g m −1 s−1. Wind speed at 1 m height was 7.2 m s−1. We had no information on the threshold-friction velocity and friction velocity. We estimated these parameters from Reference Pomeroy and GrayPomeroy and Gray's (1990) semi-empirical relationships:




We neglected the terminal fall-velocity variations with height and propose a mean value of σs U F estimated from the experimental data used by Reference Mellor and FellersMellor and Fellers(1986). In order to reproduce Takeuchi's experiment No. 3 numerically, we used the following parameters: σs U F = 0.28 m s−1, u* = 0.42 ms−1,u *t = 0.36 m s −1 and C max = 0.248 kg m −3. Figure 1 shows the numerical results obtained in the saltation layer and in the suspension layer, with a value of ρA = 7 × 10−4. Figure 2 shows the vertical variations of the concentration at different distances from the start of snow transport. These numerical results (Figs 1 and 2) are close to those of Takeuchi.

Fig. 1. Change in particle concentration in the saltation and suspension layers as a function of ablation length.

Fig. 2. Change in particle-concentration profile in the suspension layer as a function of the height at different distances from the starting point.
Deposition Flux
The deposition flux is proportional to the particle-settling velocity and to the particle concentration. But it is modified by the turbulence of the flow. At u
* = u
*t, the deposition is equal to zero. At u
* = 0, deposition occurs with its maximum value (= U
F
C). The force exerted by the flow on the particle is proportional to ![]() ; therefore, we suggest that the deposition flux could be estimated by the following model:
; therefore, we suggest that the deposition flux could be estimated by the following model:

It is essential to compare the numerical results with field experiments. But, as a first step, it is really interesting to compare the numerical results with wind-tunnel experiments where all physical processes can be measured and controlled. In this way, we can know the terminal fall velocity and the threshold friction velocity accurately and can control the friction velocity, which remains constant during the whole experiment. In our laboratory, a 13 m long wind tunnel has a 5m test area of uniform cross-section 100 × 50 cm and it is protected by a filter in order to retain the particles. The wind tunnel is equipped with a hot-film probe (one- and two-dimensional), installed on a support with three-dimensional displacement. This system allows us to measure the flow velocity and turbulence energy. A laser diode measures the height of the deposit. The measured height of the boundary layer is approximately 20 cm. Therefore, obstacles placed in the wind tunnel must not be higher than 4−5 em (height of the logarithm zone).
In order to test the deposition flux, the numerical simulations were performed for a 4cm high solid fence with a 1 cm bottom gap. The models of erosion–deposition depend on: turbulent-friction velocity, threshold-friction velocity and the settling velocity.
We have therefore tested the influence of each of these factors. One supplementary test was carried out in order to evaluate the influence of the presence of particles on the turbulence model.
First, using the numerical model, with a mesh (200 × 200 cells), we studied the variation of the leeward and windward drifts from the beginning to steady state. We noticed that the windward and leeward drifts form simultaneously in the wind tunnel.
Next, using the numerical model, we studied (Fig. 3) the influence of u */u *t on snowdrifts at equilibrium. We observed that the leeward drift is very sensitive to this parameter: it appears for u */u *t close to 1 and it disappears completely for u */u *t > 1.2. This could explain the difficulties in reproducing leeward drift in a wind tunnel (Reference Naaim-BouvetNaaim-Bouvet, 1997). The windward drift is less sensitive; the accumulated volume increases as u */u *t decreases, as previously observed in a wind tunnel for the drift of sawdust generated by a solid fence (height H) with a bottom gap (0.2H) (Reference Naaim-BouvetNaaim-Bouvet, 1997) (Fig. 4).

Fig. 3. Variation of equilibrium drift shape as function of u */u *t

Fig. 4. Experimental results obtained in a wind tunnel for different friction velocities.
The settling velocity does not affect the final profile of the drift. But the formation time depends on this parameter. The snowdrift forms rapidly if the settling velocity is important. In Figure 5, we show two snowdrifts formed in 30 minutes at two different settling velocities.

Fig. 5. Drift obtained for two different settling velocities in 30 minutes.
We have tested two turbulence models, the classical κ–ϵ model and the modified κ–ϵ model proposed by Reference Chen and WoodChen and Wood (1985), taking into account the influence of the particles (Fig. 6).

Fig. 6. Test of the two turbulence models for (u*/u*t) = 1.05.
The difference between results obtained using the two models is very small. For the same initial conditions, the snowdrift generated by the modified κ–ϵ model is slightly more extended than that generated by the κ–ϵ model. Indeed, in the modified κ–ϵ model, the presence of particles produces a diminution in the friction velocity near the ground. The zone covered by the deposit (u* < u*t) is therefore larger than that obtained by the classic κ–ϵ model.
Finally (Figs 7 and 8), we have reproduced numerically some experiments obtained using a wind tunnel. In the two cases presented, the shapes of the numerical snowdrifts and the experimental snowdrifts are relatively similar. In the case of numerical simulation, the leeward snowdrift is less important. Near the fence, the experimental leeward and windward snowdrifts are steeper than those obtained numerically. We can attribute this phenomenon to numerical diffusion and also to the inadequate mesh in the high-slope zones. The mesh is very deformed in these zones. The solution should be using a mesh orthogonal to the drift in order to reduce the numerical diffusion.

Fig. 7. Comparison between numerical and experimental results (u* = 0.25 m s−1 and u*t = 0.21 m s−1).

Fig. 8. Comparison between numerical and experimental results (u* = 0.23 m s −1 and u*t = 0.21 m s −1).
The windward snowdrift localization is well reproduced by the model. In the case of u * = 0.25 ms −1 and u *t = 0.21 m s−1, the numerical snowdrift begins at the same place. In the case of u * = 0.23 m s −1 and u *t = 0.21 m s−1, it begins slightly upstream. Numerical and experimental snowdrift lengths are very close. In the case of u * = 0.25 ms−1 and u *t = 0.21 m s−1, the numerical snowdrift is longer than the experimental one but in the case of u * = 0.23 m s −1 and u *t = 0.21 ms −1 it is shorter.
Concluding Remarks
In this paper, assumptions and preliminary results of a numerical model of snowdrift are presented. This model is based on continuum theory and erosion and deposition fluxes. It provides numerical results that are in good agreement with observed data taken around a snow fence. Variations in snowdrift formation are correctly simulated. We tested the model in the case of a 4 cm high fence with a 1 cm high gap. Unlike the windward accumulation, the leeward accumulation is very sensitive to the ratio (u */u *t). It appears for (u */u *t) close to 1 and disappears for (u */u *t) > 1.2). The global accumulation produced by the fence increases as (u */u *t) decreases. The back reaction of particles on turbulence slightly extends the windward accumulation. In spite of these good results, expression of the erosion flux must be re-examined in order to improve it. It will be necessary to carry on with experiments similar to those undertaken by Reference TakeuchiTakeuchi (1980) or to determine the splash function Tor different snow qualities.









