1. Introduction
Remote-sensing data have long been used to provide information on the distribution and properties of snow. Snowcover analysis in mountainous regions is required for various purposes such as snow mapping, meteorological modeling, climate studies, estimation of stored water equivalent or snowmelt runoff prediction. Some of these applications even require reliable information on the snow-covered area in near real time.
The Advanced Very High Resolution Radiometer (AVHRR) has been operationally employed on the polar-orbiting weather satellites of the U.S. National Oceanic and Atmospheric Administration (NOAA) for the last 24 years. This temporal coverage is unique and may be used for long-term studies analyzing AVHRR data archives and to maintain the program continuity of the long-term records in the future. An additional advantage of NOAA AVHRR is the high temporal resolution, whereas the medium spatial resolution is a challenge in rugged terrain with small patches of snow and a heterogeneous land cover.
Conventional classification algorithms or hierarchical threshold approaches applied to snow-cover estimation generate binarymaps containing “snow” or “not snow” information. Due to the medium spatial resolution of the AVHRR sensor of 1.1 km at nadir, each pixel potentially represents a mixture of snow, cloud, forest, rock, etc. Classification of such mixed pixels can lead to errors which render the area estimation inaccurate (Reference Daly, Davis, Ochs and PangburnDaly and others, 2000). These errors are caused by the classification premise that all pixels are pure, i.e. consist of a single ground-cover type or clouds, while in fact they are not.
There are many studies dealing with the development of methods to map snow cover at sub-pixel scale (Reference Nolin, Dozier and MertesNolin and others, 1993; Reference Solberg, Andersen and SteinSolberg and Andersen, 1994; Reference Painter, Roberts, Green and DozierPainter and others, 1998; Reference Simpson, Stitt and SienkoSimpson and others, 1998; Reference Metsämäki, Vepsäläinen, Pullinainen and SucksdorffMetsämäki and others, 2002; Reference Vikhamar and SolbergVikhamar and Solberg, 2002). The linear spectral mixture algorithm is a widely used technique for the decomposition of mixed pixels. It has the advantage of offering a straightforward approach which provides a physically meaningful measure of abundance that is portable across sensors and through time (Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others, 1998). Although mixture analysis was originally developed for sensors with a great number of bands, it has been successfully adapted to AVHRR data for various fields of application (Reference DeFries, Hansen, Steiniger, Dubayah, Sohlberg and TownshendDeFries and others, 1997). The algorithm has been proved to be well suited for snow-cover analysis using AVHRR data (Reference Simpson, Stitt and SienkoSimpson and others, 1998; Reference Daly, Davis, Ochs and PangburnDaly and others, 2000). Recent studies have contributed to an improvement in subpixel analysis for snow-cover estimation and are focused on a specific subject of snow-cover fraction retrieval (e.g. varying snow grain-size or snow-cover detection in the forested area). Several studies mapping montane snow cover at subpixel scale have yielded generally acceptable results (Reference Rosenthal and DozierRosenthal and Dozier, 1996). Accordingly, the linear mixing assumption is appropriate for mapping alpine snow cover at sub-pixel resolution. Most of the approaches including the linear spectral mixture modeling are supervised techniques and meet the requirement of being a procedure without any human intervention.
In this paper, we describe and validate a fast, simple solution for the operational retrieval of snow-covered area at sub-pixel scale using the linear spectral mixing algorithm.
For this purpose, several features are combined:
-
1. principal component analysis (PCA) to reduce the dimensions of the dataset;
-
2. classification into two types of end-members, “snow” and “snow-free”;
-
3. inclusion of the reflective part of AVHRR channel 3.
Together, these reduce the number of computations required for operational and near-real-time processing without human intervention using the high temporal resolution of NOAA AVHRR.
2. Data
The Remote Sensing Research Group at the University of Bern, Switzerland, has for many years received and archived NOAA AVHRR High Resolution Picture Transmission data covering the whole of the European Alps. The AVHRR scanner has five spectral bands measuring reflected solar (visible and near-infrared) energy and emitted thermal energy from the Earth's surface and the atmosphere. In this study, we deal with channels 1 (0.6 μm) and 2 (0.9 μm) in conjunction with channel 3A (1.6 μm), respectively, with the reflective part of channel 3 (3.7 μm). The pre-processing includes calibration, georeferencing and atmospheric correction of the visible channels. Atmospheric correction is based on the Simplified Method for Atmospheric Corrections (SMAC) algorithm (Reference Rahman and DedieuRahman and Dedieu, 1994). Atmospheric parameters are derived from the U.S. National Centers for Environmental Prediction (NCEP) datasets and from the Alpine Model (aLMo) of the Swiss Federal Office of Meteorology and Climatology (MeteoSwiss), whereas the atmospherical aerosol content is extracted from the same AVHRR dataset processed. The reflective part of channel 3 on NOAA-12, -14 and -15 is calculated based on Reference Baum and TrepteBaum and Trepte (1999). The local topography with varying slope and aspect is taken into account in computing the bidirectional reflectance distribution function (BRDF) based on the method presented by Reference Wu, Li and CihlarWu and others (1995). Datasets are orthorectified, so as to take into consideration the geometric distortions introduced by the complex relief and the scan geometry. Cloud detection and masking is done using the Cloud and Surface Parameter Retrieval (CASPR) package (Reference KeyKey, 2002).
3. Algorithm
Linear mixture modeling (Reference Adams, Smith and JohnsonAdams and others, 1986) is based on the assumption that the signal received at the sensor is composed of a linear mixture of pure-element reflections called end-members. The weights of these end-members represent the percentage of the pixel area occupied by each surface-cover type. The weighting coefficients (fractions) are constrained to be non-negative and sum to one. The system can be solved by a least-squares solutionwhich minimizes the unmodeled sum of squares of errors.
An accurate estimation of end-member spectra is crucial to a successful application of the linear mixture model. As listed by Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others (1998), end-members can be derived fromthe data themselves (image end-members), from a spectral library or from field reflectance measurements (reference end-members). In this paper, image end-members are used.We follow the concept of multiple end-member combination introduced by Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others (1998).
3.1. Estimating data dimensionality
The method is designed to use the first three AVHRR channels, including the purely reflective channels 1 and 2 and additionally channel 3A. The reflective part of channel 3 of the AVHRR sensor is necessary to involve the NOAA-12, -14 and -15 overpasses in the unmixing procedure. It represents an additional channel carrying essential information for the differentiation of snow and other surface-cover types and clouds.
Some studies, particularly for vegetation, include AVHRR thermal channels 4 and 5 in the unmixing process (Reference Mücher, Steinnocher, Kressler and HeunksMücher and others, 2000), although thermal emission is converted to temperature by the non-linear Planck function. This does not accomplish the assumption of linearity, on which the unmixing model used in this study is based. In this sense, only the reflective channels of the AVHRR sensor are integrated in the linear mixing algorithm.
PCA is used to transform a set of correlated variables (channels) into a new set of uncorrelated variables. It is performed on channels 1, 2 and 3A, respectively, with the reflective part of channel 3. This technique aims to compress the dataset, to remove spectral redundancy and to improve the spectral separability. Alternatively, independent component analysis (ICA) could be used as another multivariate data-driven analysis technique which is capable of decomposing any signal, considering the fractions as unknown and random quantities (Reference Chang, Chiang, Smith and GinsbergChang and others, 2002). Its application to remote-sensing data has recently been investigated and it may replace PCA once its performance on multispectral data has been evaluated against the PCA algorithm.
By definition the first two eigenchannels of the PCA contain the great majority of the total variance and thus pack >90% of the variance from the three input channels. This predefinition is important to reduce the data dimensionality into a single plane in order to calculate a two-dimensional polygon, which bounds the data space. The PCA method requires no a priori knowledge of the dataset or spectral properties of the surface types within the scene.
3.2. End-member determination from convex hull
The PCA transformation enables a graphical extraction of pixels representing the outer lines of the polygon surrounding the data space of the first two principal components (Fig.1). In the presented example of the NOAA-17 overpass, 19 end-members were determined fromthe convex hull and are labeled with circles in Figure 1. Due to illustration facilities, greater circles correspond to clusters of end-members. The scattergram produces nearly a ternary diagram with several points lying on the lines along the triangle.The concept of convex geometry, introduced by Reference Settle and DrakeSettle and Drake (1993), assumes that these points have the most pure pixel spectra whereas mixed pixels lie within the data cloud. One of the limitations of such an approach is that data clouds without straight lines along the edges cannot be fit uniquely. Also, any surface type occurring in the same proportion in every pixel is not extractable using this method, which would not include a “true” snow end-member and Foppa and others: Snow mapping over the Alps would miscalculate the snow fractions (Reference Tompkins, Mustard, Pieters and ForsythTompkins and others, 1997).
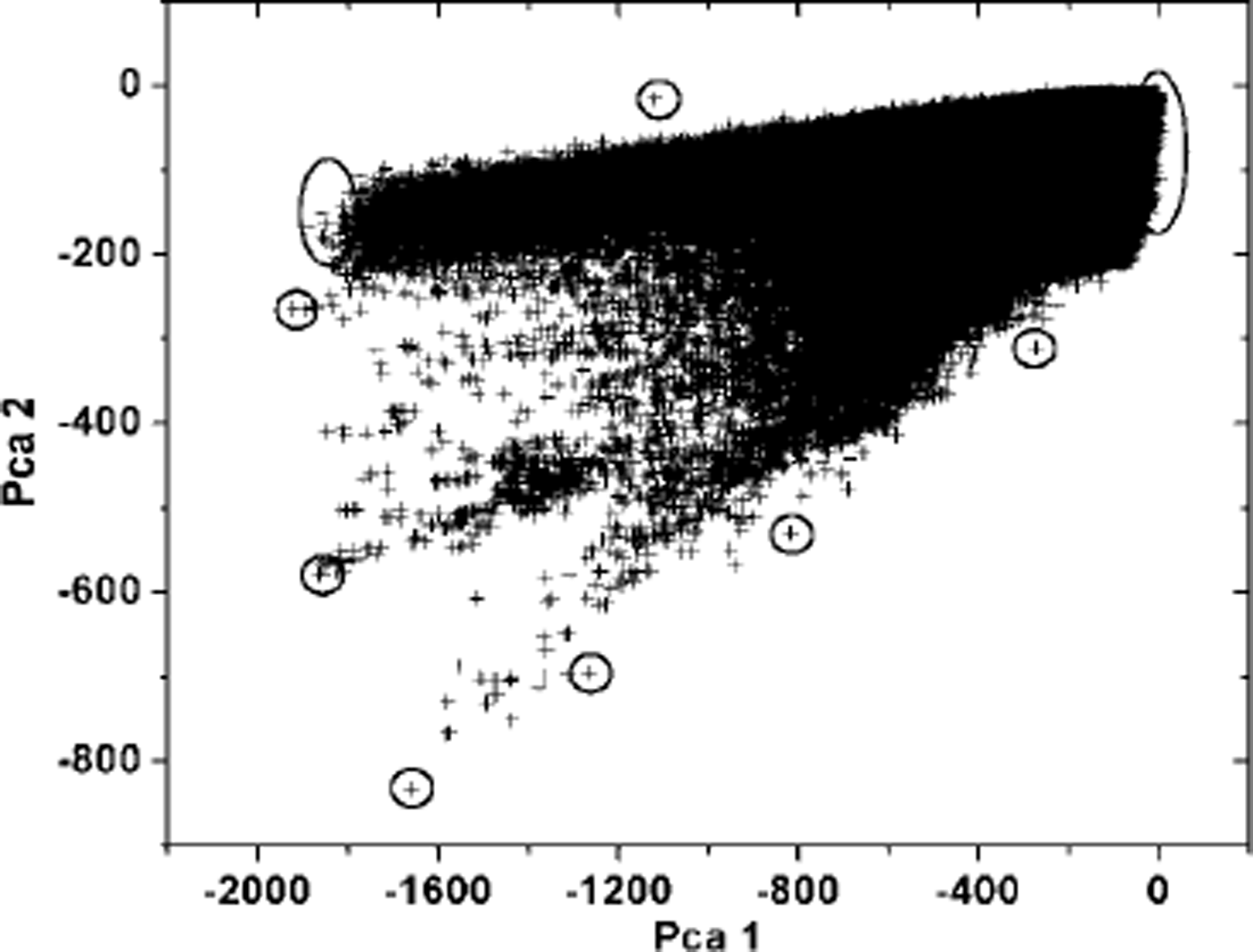
Fig. 1. Two-dimensional scatter plot using the first two principal components from NOAA-17, 17 January 2003. The extreme points, surrounded by circles, bound the cluster of pixels in the feature space.The corresponding pixels are defined as image end-members following the concept of convex geometry.
3.3. Identification of end-member spectra
The information inherent in the points representing the convex hull is not enough to assign a land-cover type to each spectrum. Figure 2 shows the spectra curves fromthe different image end-members collected from the convex hull of the dataset from the NOAA-17 noon pass on 17 January 2003. In general, the curves differ significantly from each other. Several spectra have a similar reflectance level and the curves nearly coincide, as a result of similar surface materials. Sunlit snow has a unique spectral signature, and only potential cloud spectra resemble the snow signatures with high reflectances in AVHRR channels 1 and 2. Some signatures clearly represent snow and differ substantially from other pure spectra, mainly due to channel 3A. This leads us to define an arbitrarily selected range of values (dashed lines in Fig. 2) to determine which of the potential image end-members correspond to a snow reflectance and represent a snow-image end-member. By definition, all end-member reflectance spectra lying within this range are snow-image end-members.
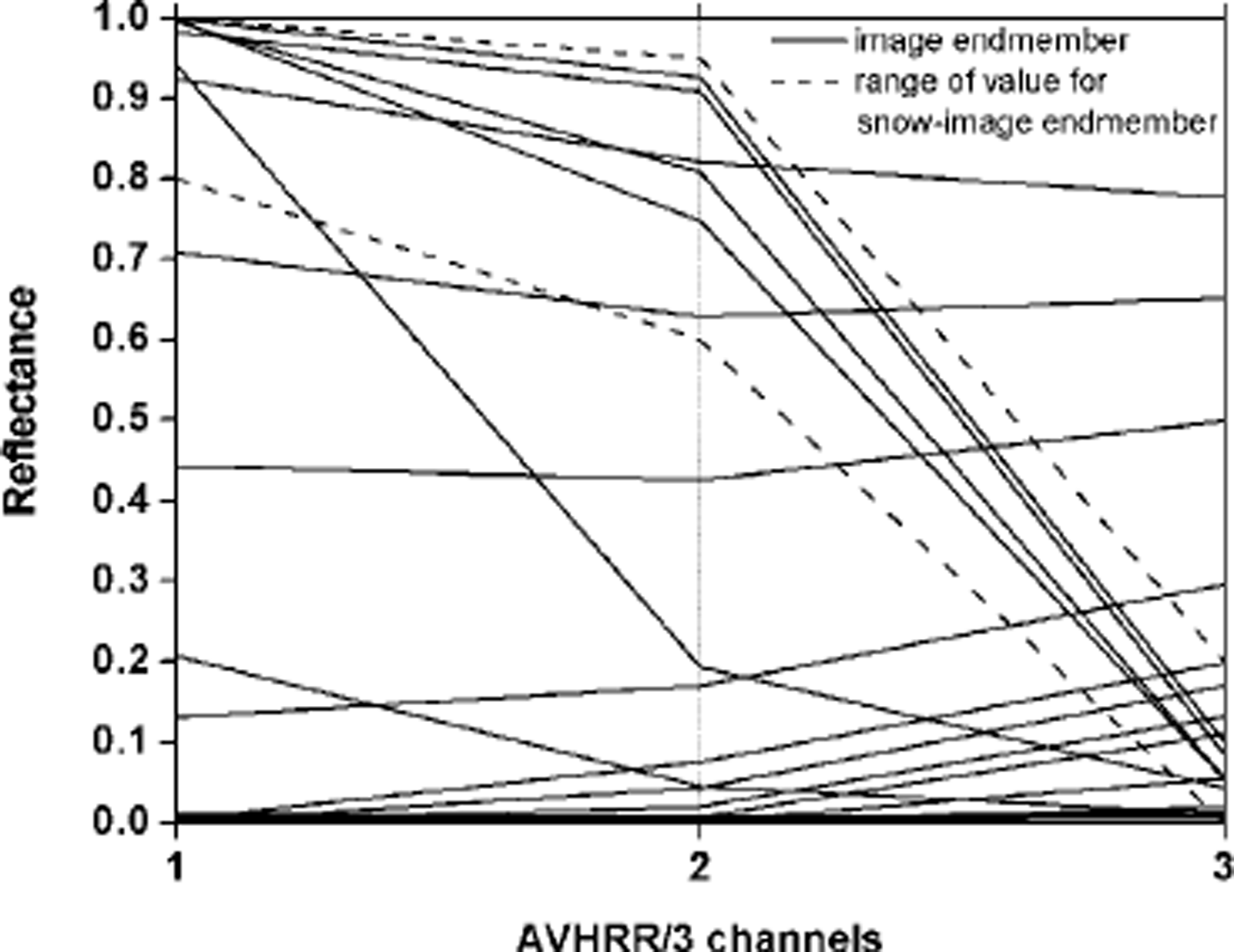
Fig. 2. End-member spectra from convex hull (NOAA-17, 17 January 2003).
To take into account the local variation of end-member spectra, Reference ChettriChettri and others (1997) suggest using an average spectrum of several pixels derived from the extremes of the polygon, instead of a single spectrum value.We calculate a mean average of all potential snow spectra, taking into account the different snow reflectances which result from variations in elevation and exposure of snow surfaces in alpine terrain (Reference Painter, Roberts, Green and DozierPainter and others, 1998) and from minimal end-member impurities. As seen in Figure 2, the snow end-members show some variability of their spectra, and the greatest differences occur in the near-infrared (channel 2), which is sensitive to moderate amounts of impurities in the snow because absorbing particulates affect snow reflectance out to 0.9 μm (Reference Grenfell, Perovich and OgrenGrenfell and others, 1981). The snow-image end-members determined correspond to reflectances from distinct geographic locations within the study area. They are distributed over the western Alps above the timberline at altitudes >2000 m a.s.l. The locations of these end-members are reasonable and therefore representative for pure-snow end-members.
3.4. Multiple end-member combination and model selection
The maximum number of end-members is limited by the number of spectral bands of the sensor used. Using three NOAA channels, either end-member pairs or triples could be constructed. The use of end-member pairs is computationally less demanding but runs the risk of partitioning unmodeled end-members into fractions, creating a fraction error. Sets of image end-member pairs are built consisting of the calculated snow end-member and another unknown image end-member which is not further analyzed. The number of end-members and the snow-image end-member are fixed, whereas one end-member type is allowed to vary. These end-member combinations are used to describe the various mixed pixels in the dataset. Creating multiple end-member combinations takes the inherent variability of an image pixel more effectively into consideration (Reference Roberts, Gardner, Church, Ustin, Scheer and GreenRoberts and others, 1998). The dataset is unmixed using all end-member pairs. The output of each mixing model is a fraction image of the unknown end-member and the snow end-member. In addition, a root-mean-squared (rms) error image represents the modeling error for each pixel. The rms error is the only indicator by which the model can be judged. The fraction of snow in a specific pixel corresponds to the model with the lowest rms for this pixel.The rms error explains how well the individually predicted pixel spectra match the data. A visual investigation reveals the spatial patterns of the rms error, and highlights where the model has not been constructed correctly.
A small rms error indicates a mathematically good model fit, and a large rms error explains a failed model construction. However, the rms error gives no information about the accuracy of the fraction image compared to the reality. A certain amount of error is inevitable and may be caused in various ways. First, the spectral property of the sensor allows only a few end-members to be used to describe the mixture of materials included in a pixel spectrum. Secondly, a small number of channels under sample the spectra, so materials with different reflectance spectra can yield in distinguishable reflectance in the bands that are imaged (Reference SmallSmall, 2001). Thirdly, the error residual for each pixel can be explained by the interaction of reflection between materials. The assumptions of linear mixing models fail to take account of non-linear mixing effects. Non-linear mixing occurs when radiation interacts with several surfaces, and is needed when, for example, forest canopy reflects radiation to the snow-covered ground (Reference Vikhamar and SolbergVikhamar and Solberg, 2002). Fourthly, residuals may also be produced by illumination variations caused by topography. Furthermore, atmospheric effects and sensor noise can affect the rms error (Reference Roberts, Smith and AdamsRoberts and others, 1993).
3.5. Post-processing
The post-processing takes into consideration the influence of the modeling constraints (fractions are non-negative and sum to one) in combination with the theoretical assumption that each pixel spectrum must be described by only two end-members. The two-end-member model forces the pixel spectrum to be unmixed, with only two end-members, one of which is a snow spectrum, which might not even exist in the selected pixel. Figure 3 displays the frequency distribution of snow-cover proportions from all cloud-free pixels in the daily composite dataset. As canbe seen in the histogram, only the non-snow end-members are labeled snow-free. The histogram of pixels from several areas expected to be totally snow-free has a normal distribution pattern of snow-cover fraction values. Using the snow-cover fraction of the peak at the lower end of the snow-cover fraction scale, one can estimate the width of the normal distribution. We define the threshold as twice the snow cover fraction of the peak. According to Figure 3, with a peak at about 7–8% snow-cover fraction, this leads to a threshold of 15%. All pixels with a lower snow-cover fraction are labeled snow-free.

Fig. 3. Histogram showing the frequency of occurrence of snow-cover fraction values from the NOAA sub-pixel composite image acquired on 17 January 2003.
4. Results and Discussion
4.1. Daily composite
Snow-cover fraction maps from NOAA-16 and NOAA-12 overpasses acquired on the same day, like NOAA-17, have been used to produce a 1day composite (Fig. 4). This overcomes the disadvantage of cloudy pixels and incorporates ephemeral snow cover. Each snow-fraction value in the composite map corresponds to the maximum snow-fraction value of the three outputs (MaxSnow). The final sub-pixel snow map shows a differentiated snow distribution with higher snow-cover fraction values over the Alps and in the region of the Bohemian and Bavarian forest in the north-east of the image. The detailed snow-cover information at subpixel scale makes it easy to recognize the complex topography of the alpine terrain with smaller and larger inner-alpine valleys. The snow-cover fraction map illustrates a snow-cover dependency on altitude with an expected snow gradient. The result of the sub-pixel process seems to be reliable for this example, and a detailed discussion is presented in section 4.2. The short processing time enables it to be used for operational applications and for long-term studies analyzing AVHRR data archives.

Fig. 4. Snow-cover fraction daily composite map as a result of the applied sub-pixel algorithm on three NOAA overpasses (N12, 14:42 UTC; N16, 13:19 UTC; N17, 11:00 UTC) from17 January 2003. Most of the values result from the NOAA-16 unmixing output because of the great number of cloud-free pixels over land. NOAA-17 and -12 contribute about 20% to the daily sub-pixel snow map. The image shows the whole European Alps (44–49° N, 5–15° E) covering an area of approximately 600 km by 800 km. The snow-cover fractions have been aggregated into four classes; the 0–15% class represents snow-free areas as discussed in section 3.5. Pixels corresponding to clouds and water bodies are masked out and occur in a pattern signature.
4.2. Comparison based on MODIS data and on classic binary mapping
To assess the strengths and weaknesses of the presented algorithm, we focus on a smaller area of interest. This region is part of the central Alps and is approximately 250 km × 250 km2 in area. The subset is shown in Figure 5 and is mostly situated in western Switzerland, characterized by a wide range of elevation zones including different land cover types.

Fig. 5. Snow-cover products and a MinRMS image generated from 17 January 2003: (a) MODIS daily snow product (MOD10A1) at 500 m resolution, co-registered to the AVHRR dataset; (b) binary snow-cover composite from separated NOAA-16 and -17 unsupervised ISODATA classification; (c) subset of the snow-cover fraction daily composite map; (d) MinRMS error map, appropriate to (c). The region of interest is situated in the central Alps and covers an area of approximately 250 × 250 km2. The subset is mostly situated in western Switzerland, characterized by a wide range of elevation zones including different land-cover types. The northwest part of the image is dominated by the Jura mountains (about 1500 m a.s.l), with the lower altitudes of the Swiss Plateau (about 600 m a.s.l.), ending in the foothills of the higher central Alps (up to 4500 m a.s.l.), covering the middle part of the subset. The dotted line in (b) and (c) represents the transect shown in Figure 6. Encircled areas correspond to specific areas of interest which are further explained in section 4.
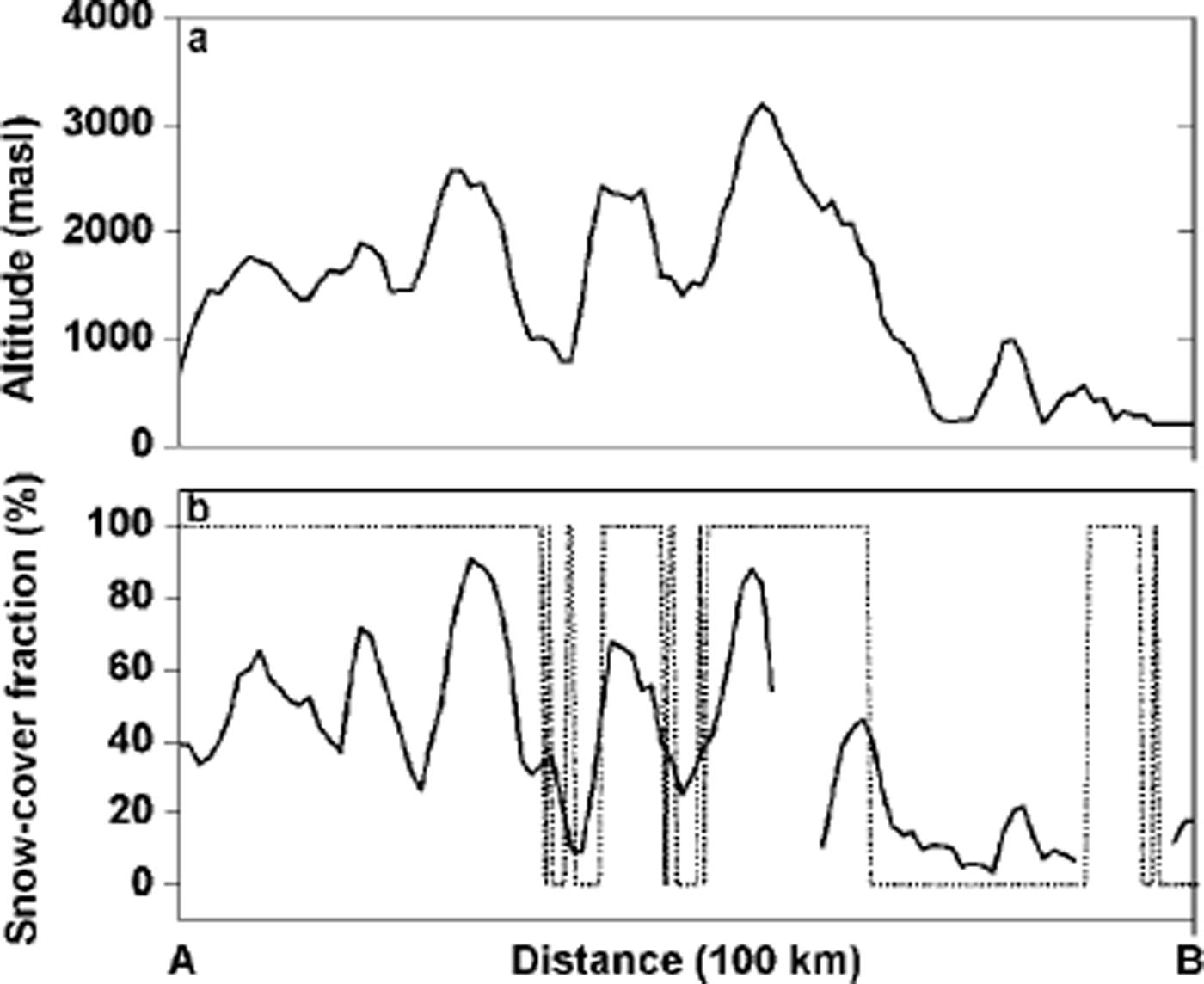
Fig. 6. Transect crossing the Bernese Alps (A) to Lake Maggiore (B). (a) The altitude along the transect; (b) the snow-cover fraction of the proposed sub-pixel method (solid line) and the MODIS snow cover (dotted line).
Snow-cover fraction maps are difficult to validate due to the lack of useful datasets (Reference Hall, Riggs, Salomonson, DiGirolamo and BayrHall and others, 2001; Reference Metsämäki, Vepsäläinen, Pullinainen and SucksdorffMetsämäki and others, 2002). We use a satellite-derived daily snow-cover product from NASA's Earth Observing System Moderate Resolution Imaging Spectroradiometer (MODIS) to compare with our sub-pixel snow map of 17 January 2003. The MODIS daily snow product at 500m resolution (MOD10A1) maps maximum snow cover of a day based on one or more passes using the normalized-difference snow index (NDSI) (Reference Hall, Riggs, Salomonson, DiGirolamo and BayrHall and others, 2001). The quality-assurance information indicates that the overall snow is mapped with reasonable accuracy. The MODIS snow map has been co-registered to the AVHRR composite map but has not been orthorectified, which may cause a shift of up to 2 kmin higher elevation zones of the Alps using AVHRR data. To improve the visual comparison of the classification, a 3 by 3 median filter was applied to the MODIS snow product and snow cover is shown in black (Fig. 5a).
As seen in Figure 5a, the spatial pattern of snow cover is dominated by two larger areas of snow-cover. These snow-cover regions include the lower mountain range of the Jura in the northwest, and the higher altitudes of the central Alps. These areas are characterized by a homogeneous closeness of snow-cover distribution and cover 53% of the whole subset region. Conversely, isolated snow and snowfree pixels are quite rare. Noteworthy features are the snow-free inner-alpine valleys, the Aare valley (46.7° N, 8° E), at the entrance to the Bernese Oberland, and the longer Rhone valley in the south (46.2°N, 7–8° E). A larger snow-free zone, clearly separating the two snow-covered regions, is found at the lower altitudes of the Swiss Plateau.
A binary snow-cover daily composite map was generated from the separated NOAA-16 and -17 unsupervised ISODATA classification algorithm. All five AVHRR channels have been included in the classification process clustering two classes. A 3 by 3 median filter was again used to highlight differences concerning the snow distribution (Fig. 5b). This binary snow-cover daily composite represents the result of a conventional classification algorithm. As seen in Figure 5b, the snow-cover distribution is less uniform than with the MODIS snow product, and patterns of snow and snow-free pixels disperse. Smaller valleys in the Alps and in the Jura mountains come forward, whereas the Swiss Plateau still dominates as a collective snow-free region. The total snow-covered area is significantly smaller than with the MODIS product and only 36% of all pixels are mapped as snow.
The subset of the snow-cover fraction daily composite map in Figure 5c shows the advantage of the implemented algorithm following from the additional information on snowcover at sub-pixel scale. Due to this, a distinct snowline separating snow-covered from snow-free areas as seen in Figure 5a and b is not located. The subset of the snow-cover fraction daily composite map includes the defined threshold of 15% snow-cover fraction. Due to illustration facilities, snow-cover fraction values below the threshold and masked areas of cloud and water are merged. Contrary to what the MODIS snow product and the classical binary algorithm suggest, the Swiss Plateau is almost completely snow-covered but with a mean snow-cover fraction of only about 26%. Weather conditions on the north side of the central Alps were characterized by snowfall and very cold air masses during the week before data acquisition. These facts point to a reasonable snow-cover distribution at these lower altitudes.
Areas where the MODIS algorithm maps snow and neither the binary nor the sub-pixel approach detects snow are mainly situated in the foothills of the northern Alps and in the French Jura. These regions, well known as areas of dense deciduous and coniferous forest, are encircled in Figure 5a-d and labeled C. The MODIS snow-mapping algorithm uses the normalized-difference vegetation index (NDVI) together with the NDSI to improve snow mapping in dense forests (Reference Hall, Riggs, Salomonson, DiGirolamo and BayrHall and others, 2001). Illuminated snow and conifer tree crowns are highly spectral-separable in the visible and parts of the near-infrared regions (Reference Vikhamar and SolbergVikhamar and Solberg, 2002). As long as snow is on the trees, the AVHRR sub-pixel algorithm estimates a higher snow-cover fraction within a pixel. The snow distribution in the forest may change over time due to wind, topography and snow interception. In addition, snow-covered ground is affected by shadow casting from surrounded trees, leading to a nonlinear mixing problem. These factors influence the reflectance and result in a snow-cover fraction <15%.
The areas mentioned stand out in the MinRMS image with the highest modeling errors (Fig.5d). This is apixel-wise composite of the minimal modeling error (MinRMS error) on which the corresponding mixing model with a certain snow-cover fraction value (Fig. 5c) is based. The MinRMS is given in per cent of the pixel spectrum and varies between 0 and 7.5% deviation. The higher modeling errors are explainable by the multiple end-member combination which lacks an end-member representing forest in all of the three overpasses. Because of this missing end-member, the mixing modeling becomes inaccurate. In general, the MinRMS is rather small, and a dependency of the modeling error on the altitude could not be assessed. A noteworthy feature is the spatial pattern of the highest MinRMS errors over the central Alps (see regions D in Fig. 5d). These pixels result from the NOAA-16 overpass and are located on higher elevation zones, situated on the south andwest slopes of the alpine mountains. The high sun-zenith angle in combination with a large satellite zenith angle influences the spectral reflectance behavior of snow. This effect enhances the degree of anisotropy of reflected snow and increases the reflectance in AVHRR channels 1 and 2 (Reference Jin and SimpsonJin and Simpson, 1999). The pixels mentioned are therefore saturated in channels 1 and 2, and unmixed use of a snow-image end-member of a lower reflectance results in higher modeling errors and tends to slightly underestimate the snowcover in these pixels.
Snow cover changes significantly with increasing altitudes and different topographic exposures, and the snow distribution is complex and variable over short distances in the alpine mountain region. To portray this effect, snow-cover fractions along a 100 km transect through the central Alps are shown in Figure 6. In Figure 5a and c the mentioned transect is plotted in dotted lines from A to B. This spatial profile ranges from northwest (A) to southeast (B), crossing several inner-alpine valleys and different elevation zones (Fig. 6a). Figure 6b visualizes the corresponding snow-fraction values in straight lines, whereas the MODIS snow-cover is displayed in dotted lines. As expected, a correlation between snow-cover fraction values and topography can be identified. Higher amounts of snow cover at sub-pixel resolution on the north side of the Alps result from the meteorological conditions days before the data were acquired, characterized by a very cold air mass with temperatures below the freezing point. By contrast, hardly any snowfall occurred on the south side of the Alps. This effect, in combination with the southern exposure of the slope, leads to a strong decrease in snow cover. The previously mentioned tendency to slightly underestimate the snow-cover at specific exposures at the highest altitudes also makes a contribution.
The sub-pixel snow distribution is quite distinct from that in MODIS. The MODIS snow algorithm reproduces the topography in a more general manner. The greater Rhone valley and the adjacent valley on the south side have been classified mainly as snow-free, whereas the pixels in the smaller northern valley are snow-covered. The snow-free region on the south of the alpine mass if is interrupted by a snow-cover area detected at the end of the transect. This feature might be due to a misclassification of low-level clouds, which were masked out during the AVHRR pre-processing. The MODIS snow algorithm classifies pixels as “snow” if the pixel reaches approximately 40% snow cover.
5. Conclusions and Future Work
PCA, including the reflective part of AVHRR channel 3, is used to estimate fractions of “snow” and “not snow” within a pixel by means of the linear mixture modeling algorithm. This combination leads to a simple, fast solution which is suitable for operational and near-real-time applications. All steps of the processing flow are well defined, objective and human interaction is not required. We have successfully mapped snow cover at the sub-pixel scale for this case study and demonstrated a substantial improvement in snow mapping over complex terrain compared to a classic binary algorithm. Even in regions and at altitudes (e.g. Swiss Plateau) where the binary classification approach does not detect snow, a certain amount of snow exists, which is mapped by the sub-pixel technique. Information on weather conditions during the days before data acquisition supports this snow distribution.
The complexity of the alpine topography is also recognized in a more precise way than when using the higher-spatial-resolution snow product from MODIS. Disagreements concerning the snow distribution are found in dense forested areas where the sub-pixel algorithm does not map fractions greater than 15%, nor does the classical approach detect any snow. In addition, the sub-pixel method overestimates snow fractions in the lowest-elevation zones, where no snow is actually expected (southern Alps). This effect results from the two-end-member model “snow” and “snow-free”, which forces the pixel spectrum to be unmixed, with only two end-members. The modeling accuracy correlates to areas representing a specific ground-cover type (e.g. forested areas), which has not been detected from the feature space of the PCA transformation using the concept of convex geometry. The modeling accuracy is further influenced by the anisotropic behavior of snow, observed over specific exposures at the highest altitudes in the central Alps, resulting in high rms errors. Overall snow is detected with reasonable accuracy at sub-pixel scale over the alpine topography using an algorithm for operational and real-time applications.
Future work will determine the efficiency of the algorithm over different seasons of the year, in order to validate the method under variable conditions and rapid environmental changes in the Alps. As a further criterion of end-member choice and model fit, one could compute the fraction over- and under-flows. Fraction overflow indicates that there were pixels in the image that were purer representations of that end-member, while fraction underflow indicates pixels that were not well represented by any of the end-members.These factors provide additional information about the mixing accuracy, but obviously complicate the procedure. To solve the problem of missing snow or snowfree image end-members, a set of reference end-members could be integrated into the multiple end-member combination to intercept unrealistic fraction estimates. These reference end-members must take the illumination-geometry and the actual satellite overpass into account.
Some adjustment of the algorithm is required to correct for the influence of the anisotropic behavior of snow, which might be a comprehensive assignment. The ICA could probably be substituted for the PCA algorithm, but it needs to undergo tests and validation on multispectral datasets to determine its suitability.
Acknowledgements
MODIS data were provided by the U.S. Geological Survey (USGS) Earth Resources Observation Systems (EROS) Data Center. The monthly weather report from the Federal Office of Meteorology and Climatology (MeteoSwiss) has been used to describe the meteorological conditions in January 2003. We gratefully acknowledge the helpful and constructive reports of the two anonymous referees and the editor, K. Nishimura.







