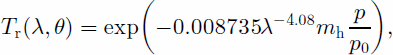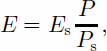Retrieval of snow reflectance from Landsat data in rugged terrain

Abstract

We developed a model to calculate the spectral reflectance of snow by normalizing the topographic effect and correcting the atmospheric effect simultaneously. This model considers the shadowing effect of the surrounding terrain on both direct and diffuse irradiance by using the obstruction coefficient in sun-ray direction and introducing the isotropic view factor. In addition, a new method to calculate the surrounding-reflected irradiance by introducing the shape factor which can account for the radiation reflected from the surrounding pixels was developed. The model was tested in the upper stream of the Heihe river basin, Qilian mountains, China, using a subscene of a Landsat Enhanced Thematic Mapper Plus (ETM+) image acquired on 20 April 2000. The result showed that the model could eliminate most of the shadowing effect of rugged terrain and could estimate snow reflectance correctly. The problem of data saturation when retrieving snow reflectance is also discussed.

Introduction

The strong variation of the altitude, slope and aspect in mountainous areas has a significant influence on snow mapping using high-resolution remote-sensing data such as Landsat Thematic Mapper (TM) and Enhanced Thematic Mapper Plus (ETM+) imagery (Dozier, 1984; Dozier and Marks, 1987). A pixel might be shadowed by the slope orientation of the pixel itself or by the surrounding terrain. In addition, the atmospheric transmissivity and optical depth vary with the quickly changed altitude and accordingly air pressure and water-vapor content, so the atmospheric correction must be performed pixel by pixel. Therefore, a combined topographic normalization and atmospheric correction is essential for quantitative retrieval of spectral reflectance of snow in rugged terrain.

Various methods of topographic normalization have been developed since the late 1970s. They can be summed up as follows:

1. (1) Band-ratio method (Holben and Justice, 1980). Much information is lost using this method, and it has seldom been used in recent years.

2. (2) Cosine-law method. This method is used by some image-processing software such as ERDAS Imagine. It often results in over-correction because it neglects the modeling of diffuse and surrounding-reflected solar irradiation. Civco (1989) developed an empirically derived modification of the cosine-law method to reduce the topographic effect.

3. (3) Minnaert method. This is very effective in slightly rugged terrain (Eyton, 1989; Colby, 1991), but the Minnaert constant is difficult to estimate according to changing Sun–Earth geometry and different spectral bands, which hinders application of the method.

4. (4) Deterministic models. These implement topographic normalization through atmospheric correction and modeling of solar irradiation using a digital terrain model (DTM) (Proy and others, 1989; Dozier and Frew, 1990; Dubayah and Rich, 1995; Li and others, 1999). The spectral reflectance is thus obtained with the Lambertian assumption (Conese and others, 1993; Richter, 1997).

In this paper, we develop a topographic normalization model whose originality lies in the deterministic methods used. The new model follows the antecedent models to calculate the spectral reflectance of snow at ETM+ bands 1–5 and 7 by normalizing the topographic effect and correcting the atmospheric effect simultaneously. The main improvement in this model is that it considers the shadowing effect of the surrounding terrain, not only on direct irradiance, but also on diffuse irradiance. In addition, it presents a new method of calculating the surrounding-reflected irradiation.

The model procedures are as follows:

1. (1) The atmospheric effect is corrected pixel by pixel using elevation-dependent functions.

2. (2) The total solar irradiance is decomposed into direct, diffuse and surrounding-reflected components. The direct and diffuse components are calculated by taking into account the shadowing effect of the north-oriented slope and of the surrounding terrain using digital elevation data. The surrounding-reflected irradiance is calculated using a shape-factor algorithm.

3. (3) The spectral reflectance is then estimated with the Lambertian assumption.

Model

Assuming the Earth’s surface is Lambertian, the spectral reflectance can be approximately expressed as

(1)

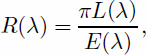
where R is the spectral reflectance, L is the radiance (Wm^–2 sr^–1 μm^–1) and E is the solar irradiance (Wm^–2 μm^–1). R; L and E are all functions of wavelength (λ). In this study, the objective is to retrieve the spectral reflectance of each ETM+ reflective band, i.e. bands 1–5 and 7. The modeling of L and E, respectively, is described in the next two subsections.

Atmospheric correction

The atmosphere in high mountainous areas is characterized by thin, clear air, less water vapor, small-sized and few aerosols. The radiative attenuation by Rayleigh scattering, water-vapor absorption and aerosol scattering is much smaller than in low-elevation regions. Accordingly, an atmospheric correction model in a mountainous area must consider the strong spatial variation of water vapor, air pressure and air temperature, which have a significant effect on the atmosphere transmissivity. Therefore, the atmospheric correction requires a modeling of spatial distribution of these factors. In this paper, we use semi-physical, semi-empirical functions to estimate the air pressure, air temperature, vapor pressure and Ångström’s turbidity coefficients of aerosol at each pixel.

The radiance reflected from a pixel can be expressed by

(2)

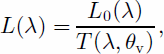
where L₀ is the at-satellite radiance (Wm^–2 sr ^–1 μm^–1) after absolute sensor calibration, and T is the transmissivity, which is a function of sensor viewing angle θ_v, wavelength λ and atmospheric conditions. For ETM+, the viewing angle θ_v = 90°. T can be expressed by (Leckner, 1978)

(3)

where T_r(λ; θ_v) is the transmissivity function of Rayleigh scattering, T_O3 λ; θ(_v) is the transmissivity function of O₃ absorption, T_w(λ; θ_v) is the transmissivity function of water-vapor absorption, and T_a(λ; θ_v) is the transmissivity function of aerosol scattering.

1. (1) The transmissivity function of Rayleigh scattering is calculated using the equation given by Robinson (1966):

   

   (4)

   where m_h is the air mass, p₀ is the standard air pressure, and p is the air pressure at the pixel, which is calculated by the pressure–elevation relationship (Wang, 1987).

2. (2) The transmissivity function of O₃ absorption can be expressed as (Zuo and others, 1991)

   

   (5)

   where –k_O3 is the absorption coefficient of O₃, and L is the O₃ amount in the vertical air column. The values of –k_O3 and L are obtained from Zuo and others (1991).

3. (3) The transmissivity function of water-vapor absorption can be expressed as (Zuo and others, 1991)

   

   (6)

   where k(λ) is the effective absorption coefficient of water vapor, and w is the precipitable water, which for China can be expressed as a simple relationship to surface vapor pressure (Zhou, 1984)

   

   (7)

   E is the absolute vapor pressure at the pixel. It can be calculated by

   

   (8)

   where E_s and P_s are absolute vapor pressure and air pressure at a meteorological station within the coverage of the ETM+ image, respectively.

4. (4) The transmissivity function of aerosol scattering is calculated using the equation given by Ångström (1964):

   

   (9)

   where β and α are turbidity parameters independent of wavelength, referred to as atmospheric turbidity parameter and wavelength parameter, respectively.

Irradiance

Global irradiance canbe decomposed into direct irradiance E_dir(λ), diffuse irradiance E_dif(λ) and irradiance reflected from the surrounding terrain E_sur(λ):

(10)

Some digital elevation model- (DEM)-based algorithms have been developed to calculate solar irradiance (Proy and others, 1989; Dozier and Frew, 1990; Dubayah and Rich, 1995; Li and others, 1999). These methods required geometric factors to account for the shadowing effect of both a pixel itself and surrounding terrain. Some scientists (Dozier and Marks, 1987; Dozier and Frew, 1990) obtained approximation solutions from analytic equations, but in this paper we use discrete methods to calculate these factors.

(1) The obstruction coefficient by the surrounding terrain V_s

V_s is defined as the percentage of a pixel obstructed by the surrounding terrain (Li and other, 1999). It is a binary function in this model because the resolution of the ETM+ image is fine. When the calculating pixel is obstructed by the surrounding terrain, V_s = 0; otherwise, V_s = 1. This algorithm proceeds as follows (see Fig. 1):

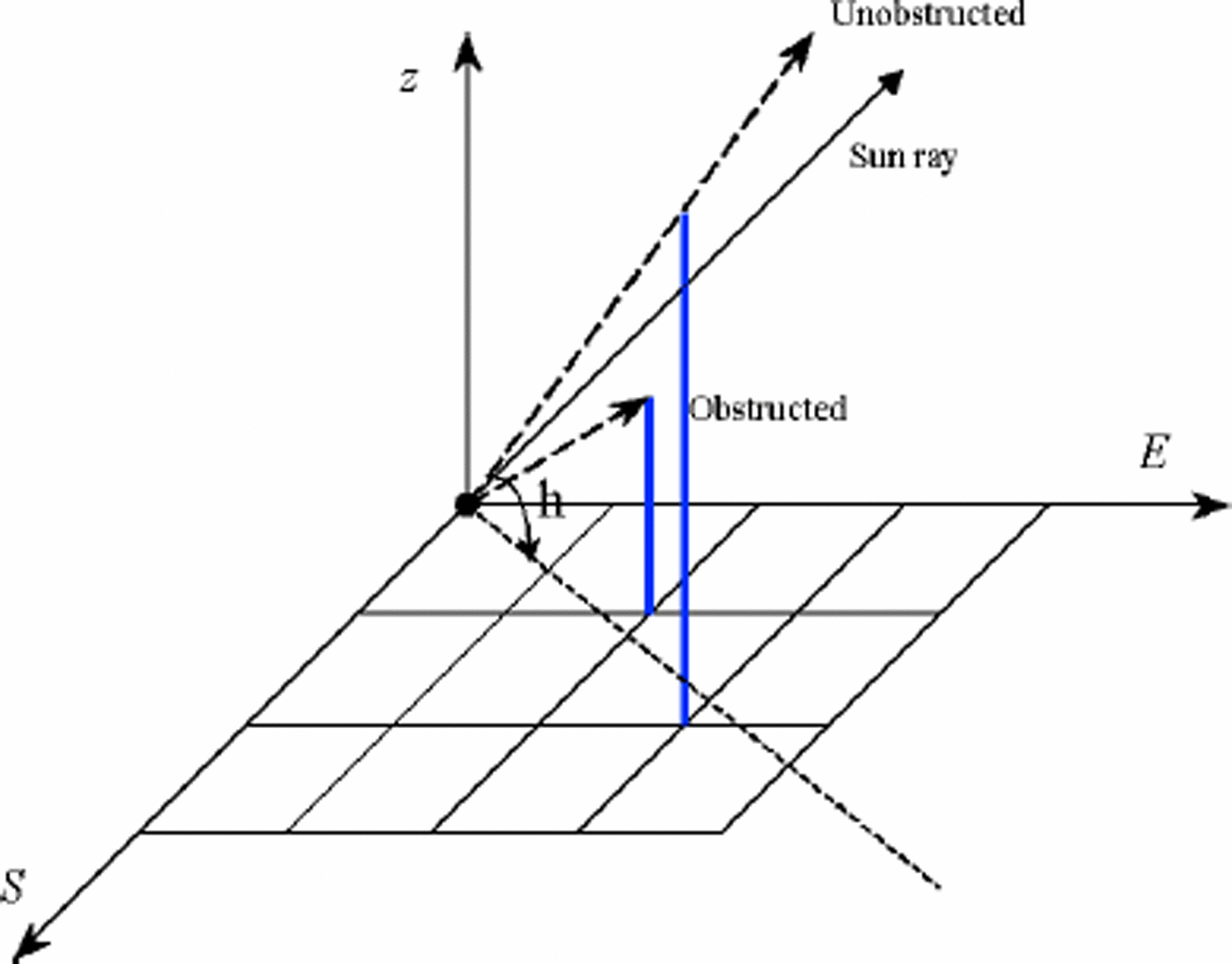
Fig. 1. Schematic diagram for the algorithm for obstruction coefficient.

1. a. Input the solar elevation, solar azimuth and tracing depth (in the unit of pixel number).

2. b. Calculate the ray-trace quadrant according to the solar elevation.

3. c. Calculate the tracing direction. If the inclinationbetween the solar azimuth and the x axis is 545°, the step in the x direction increases one; then obtain the steps in the y direction. If the inclination between the solar azimuth and the x axis is 445°, the step in the y direction increases one; then obtain the steps in the x direction. Once the tracing direction is known, the pixels along the direction are marked.

4. d. Calculate the elevation angle between the shadowing pixel and the pixels along the tracing direction successively. Once the elevation angle is greater than the solar elevation, V_s =0, then exit from the iteration; otherwise, trace to the tracing depth. If no elevation angle is greater than the solar elevation, V_s =1.

(2) Isotropic view factor V_iso

V_iso is defined as the fraction of the hemisphere that is visible from a pixel. It stands for the influence of the surrounding terrain on the isotopic diffuse radiation.

The algorithm for V_iso is as follows:

Divide the 2\ hemispheric space into n identical parts, then trace along the sun-ray along the projected vector on the xy-plane, calculate the height angle between each pixel and the starting pixel along the vector successively, and find out the maximum angle h_i which separates the sky into obstructed and unobstructed parts (Fig. 2).

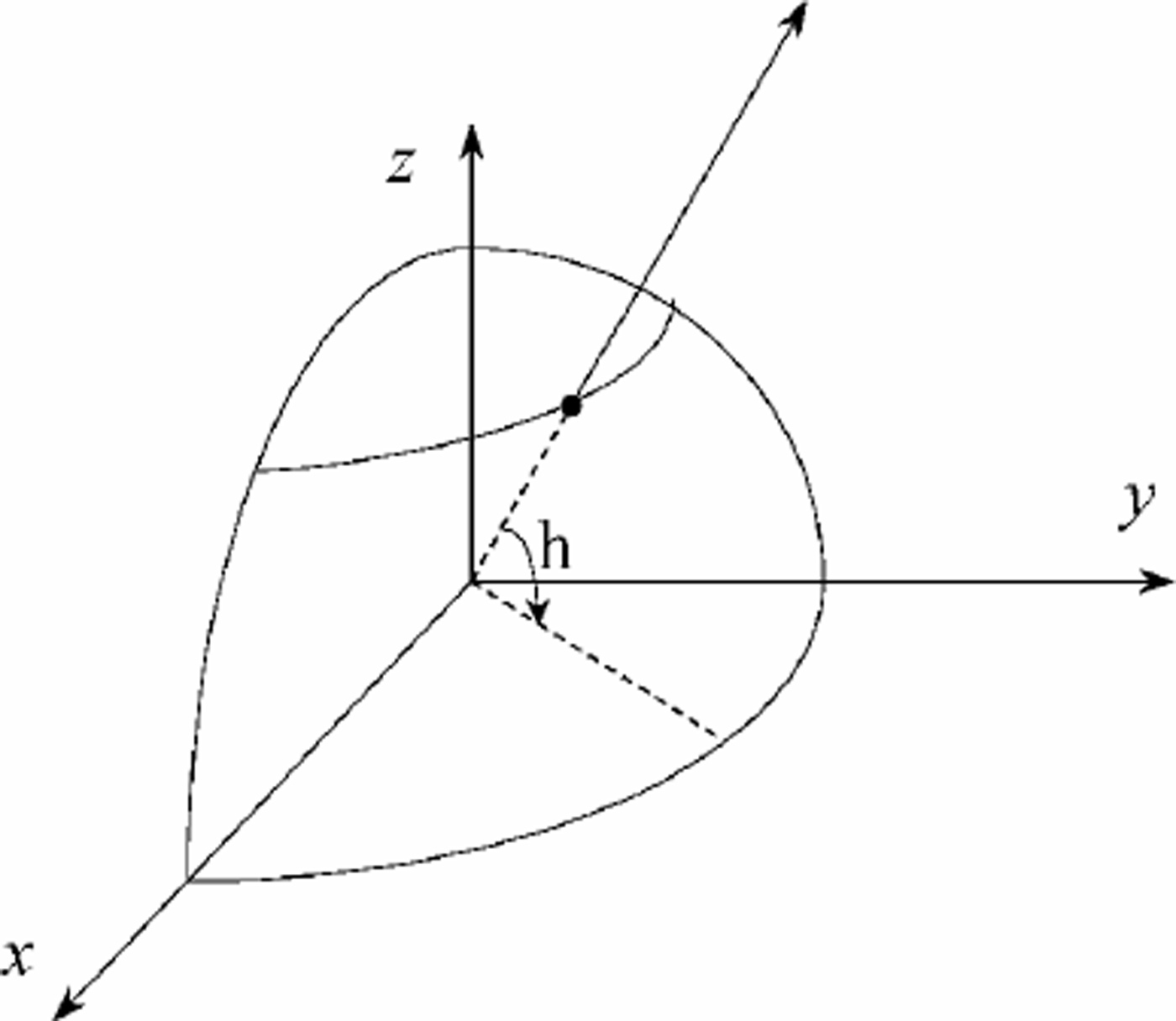
Fig. 2. Schematic diagram for the algorithm for isotopic view factor.

The area ratio (k) of the unobstructed part in the sky is (Li and others, 1999)

(11)

When the pixel is a peak or on a ridge, the ratio k can be 41.

Therefore, the isotopic view factor is:

(12)

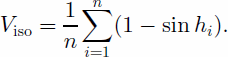
(3) Shape factor F_ij

F_ij is defined as the ratio of the energy reaching another pixel to the energy emitted from the source pixel. It is a purely geometric value depending only on topography

(Fig. 3). The shape factor between two mutually seen pixels is (Sun and Yang, 1995)

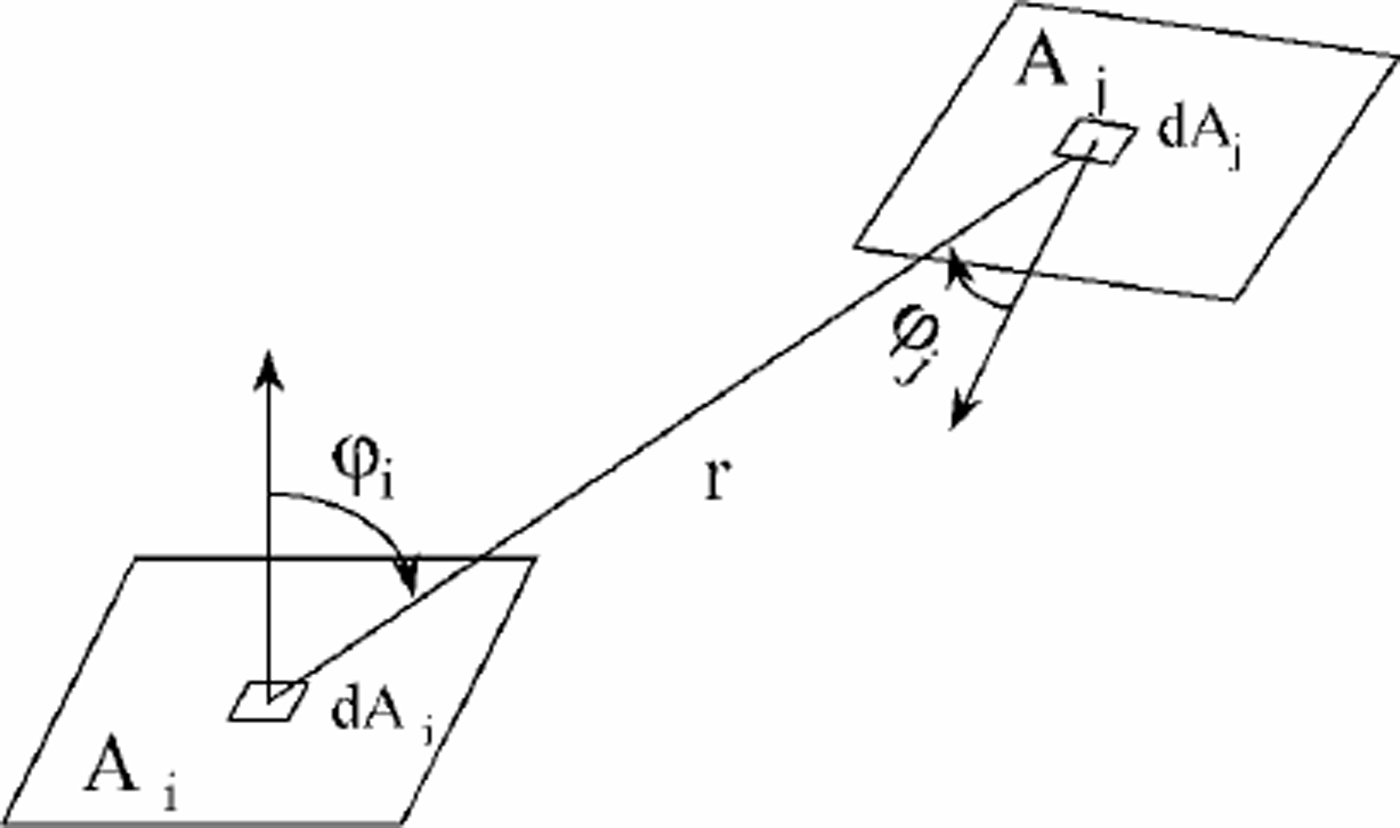
Fig. 3. Schematic diagram for the calculation of shape factor.

(13)

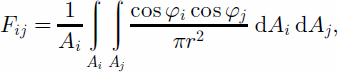
where A_i and A_j are the areas of pixels i and j, respectively, φ_i and φ_j are the intersection angles between the normal vectors of pixels i and j, and their connection line, respectively, and r is the distance between pixels i and j. When the pixel resolution is very high, the following simplified equation can be used to calculate F_ij (Proy and others, 1989; Li and others, 1999):

(14)

where d is the distance between pixels i and j with the unit in pixel numbers.

Based on the above geometric factors, the irradiance components in anobstructed environment can be expressed as

Direct irradiance

(15)

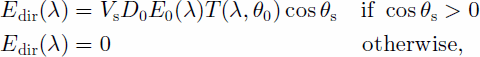
where E₀(λ) is the extraterrestrial solar irradiance, D₀ is the calibration factor for Earth orbit, which can be calculated by

the Fourier series (Zuo and others, 1991), T(λ; θ₀) is the beam transmissivity, θ₀ is the solar zenith angle, and θ_s is the angle between the solar rays and the normal to the surface. Equations to calculate θ_s can be found in many studies (e.g. Dozier and Frew, 1990).

Diffuse irradiance

By taking into account both the isotropic view factor V_iso and the obstruction coefficient in solar direction V_s, the Hay (1979) model can be modified as

(16)

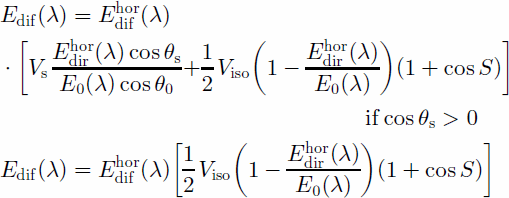
where S is the slope angle, is the diffuse radiance on the horizontal surface, as in Munro and Young (1982),

(17)

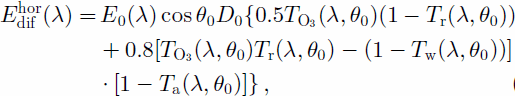
and is the direct irradiance on the horizontal surface under an unobstructed environment, calculated by

(18)

Surrounding-reflected irradiance

E_sur(λ) is calculated by

(19)

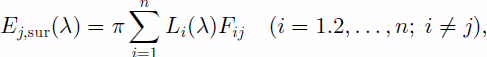
where subscripts i and j are pixel indexes, and L_i(λ) is the radiance from the ith pixel in the neighborhood of pixel j.

Study Area And Data Processing

The test area is located in the upper stream of the Heihe river basin, Qilian mountains, China, with an area of about 169 km². It is located at 37°50–37°58 N, 100°32–100°44E. According to the DEM statistic, the elevation in this region is 3240–4440m, with an average of 3824.3 m. The topography is very steep, characterized by a sharply rugged slope with an average value of 20.2° and a maximum value of about 50°. The seasonal snow cover usually lasts from September to May. Other land-cover types are shrub, cold desert, alpine meadow, short grassland and marsh. A detailed description of this region can be found in Yang and others (1992).

Topographic maps of the region, with a scale of 1:100 000 and a contour interval of 20 m, were digitized using the ARC/Info geographic information system software. The DEM was created using a triangular irregular network datamodel and then transferred into gridded data. The cell size of the DEM is 30 m, and the map projection used is Gauss–Kruger in the 1954 Beijing Coordinate System. Figure 4 is the shaded DEM of the study area produced with the same solar azimuth and zenith angles as the ETM+ image.

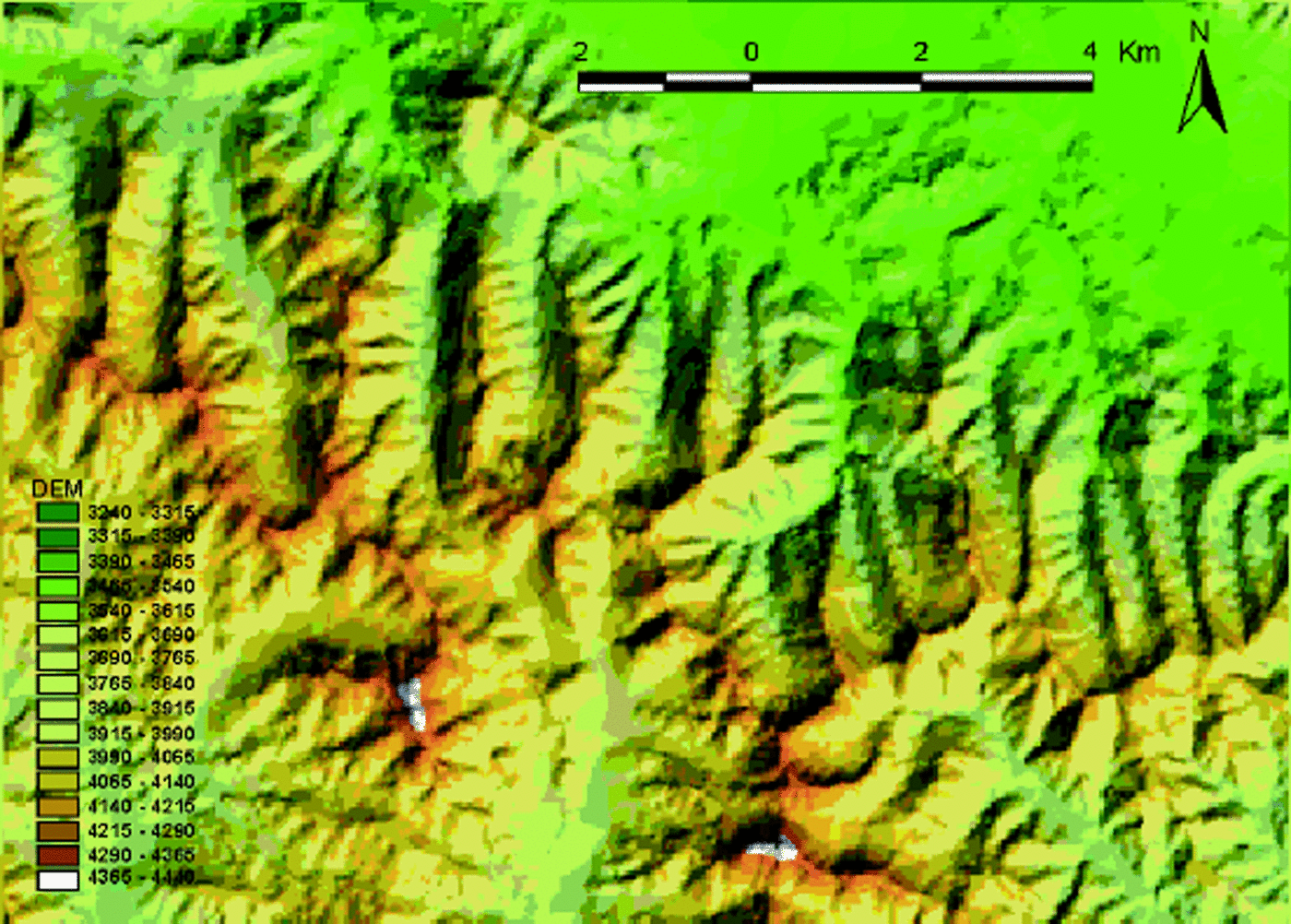
Fig. 4. DEM of the study area.

A subscene of the ETM+ image (133/34, REQ ID = 20002230591)acquired on 20 April 2000 was obtained for the study. The solar elevation and azimuth angles are 57.3° and 136.5° at the image acquisition time, respectively. Geometric correction was performed using the Simple Geometric Correction module of the image-processing software PCI. We collected 15 ground-control points from digitized topographic maps and used the bilinear method for resampling. After all the processing, the DEM and the image are co-registered with rms errors of 0.30 pixel in the x direction and 0.58 pixel in the y direction.

The observations of air temperature, air pressure and absolute vapor pressure at a meteorological station (Qilian station, 38°11’N, 100°15’ E; 2787ma.s.l.) within the ETM+ image are required as input to the model. The values of these variables are: air temperature, 4.8°C; air pressure, 722 hPa; absolute vapor pressure, 3.9 hPa. The values of Ångström’s turbidity coefficients of aerosol are estimated using observations in other high mountainous regions (Tong and Xiang, 1975). The estimation is only correct within the order of one.

Testing And Evaluation

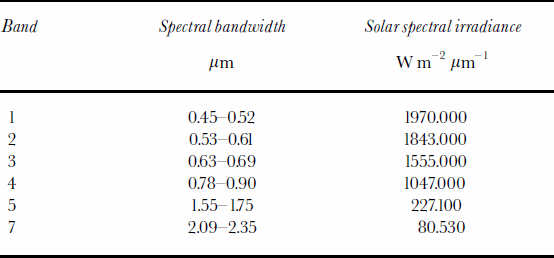
At first, the direct, diffuse, surrounding-reflected and total irradiances at the equivalent bandwidth of ETM+ bands 1–5 and 7 are calculated according to the irradiance model presented in this paper. The constants of solar spectral irradiance and other sensor parameters (Table 1) are obtained from the Landsat 7 Science Data User Handbook (NASA, 2001). Figure 5 is an example of total irradiance at ETM+ band 4. We analyze the relationship between the irradiance map and topographic maps such as the DEM, slope map and aspect map. Results show that the simulation result is very realistic in relation to terrain.

Fig. 5. Total irradiance at ETM+ band 4.

Table 1. Landsat ETM+ band characteristics

Spectral reflectance of all ETM+ reflective bands are then calculated. In Figure 6 we show the composite of ETM+ bands 4 (red), 3 (green) and 2 (blue) after topographic normalization with uncorrected composite, and in Figure 7 we compare band 5 only. We analyze the results both via a visual interpretation and through the statistic of spectral reflectance of snow before and after topographic normalization.

Fig. 6. RGB color composite of ETM+ bands 4, 3 and 2 of the study area (a) after topographic normalization, and (b) without topographic normalization.

Fig. 7. ETM+ band 5 image of the study area (a) after topographic normalization, and (b) without topographic normalization.

Visual interpretation

Figures 6 and 7 show that most of the shadowing effects, especially those in the upper right quarter of the image, are removed. In addition, with the local amplification in Figure 8 we can see some of the snow in shady slopes is shadowed, but after topographic normalization it can be clearly distinguished from other types. The shadowing effect is particularly strong in band 5 because diffuse irradiance takes up only a small proportion of this band. After removal of the topographic effects, much more detail is apparent in band 5.

Fig. 8. Local amplification of (a) Figure 6a and (b) Figure 6b.

Spectral reflectance of snow

To evaluate the model, we randomly collected the reflectance of 20 snow samples from corrected (atmospheric correction + topographic normalization) and uncorrected images from both sun-facing and shady slopes at ETM+ bands 1–5 and 7. Table 2 compares the mean value of the spectral reflectance of 20 snow samples with uncorrected apparent reflectance. Figure 9a–d show the measured spectrum of 20 corrected and uncorrected samples. These results suggest that in the uncorrected image the apparent reflectance of snow on the shady slope is very low. This is obviously untrue since we know snow reflectance is very high in visible bands (Hall and Martinec, 1985). This can be explained by the shadowing effects on shady slopes. On the sun-facing slope, there is serious data saturation in bands 1–3. Snow reflectance is much larger in band 4 than on the shady slope; this is another example of the topographic effect because if the shady and sun-facing slopes have the same snow cover and the snow accumulation is usually larger on northern slopes, the spectral reflectance of snow on different slopes should be homogeneous or on northern slopes a little larger. After atmospheric correction and topographic normalization, the snow reflectance on shady slopes is believed to show the true situation. Mean and individual values (Table 2; Fig. 9b) of the reflectance of snow on shady slopes are comparable to many in the literature (Zeng and others, 1984; Hall and Martinec, 1985). On the sun-facing slope, data saturation is a also a significant phenomenon; snow reflectance in bands 1–3 reaches asaturated value, and the standard deviation is very small. Snow reflectance in bands 4–5 and 7 is similar to the values on shady slopes.

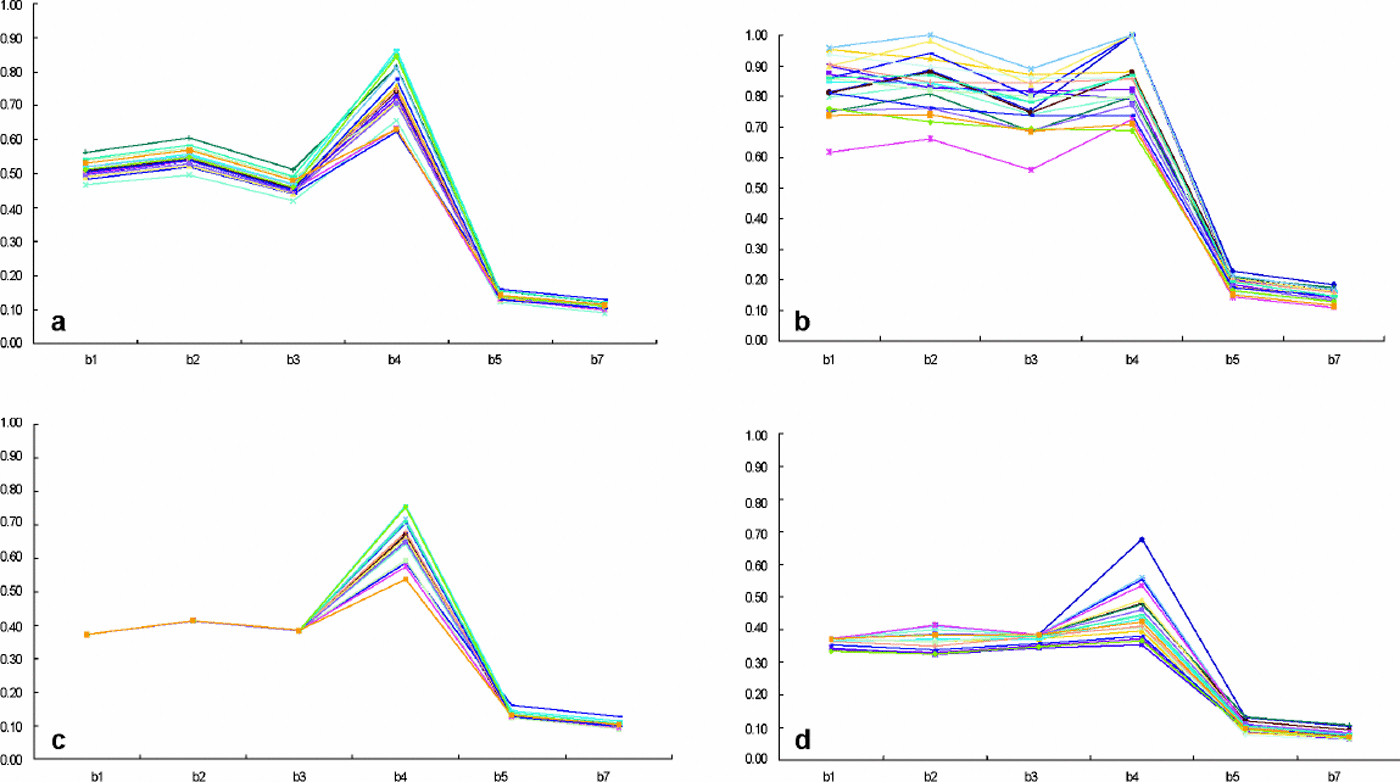
Fig. 9. Corrected spectral reflectance of 20 snow samples on (a) sun-facing slope and (b) shady slope. Uncorrected spectral reflectance of 20 snow samples on (c) sun-facing slope and (d) shady slope.

Table 2. Calculation results of spectral reflectance of snow at ETM+ bands 1–5 and 7

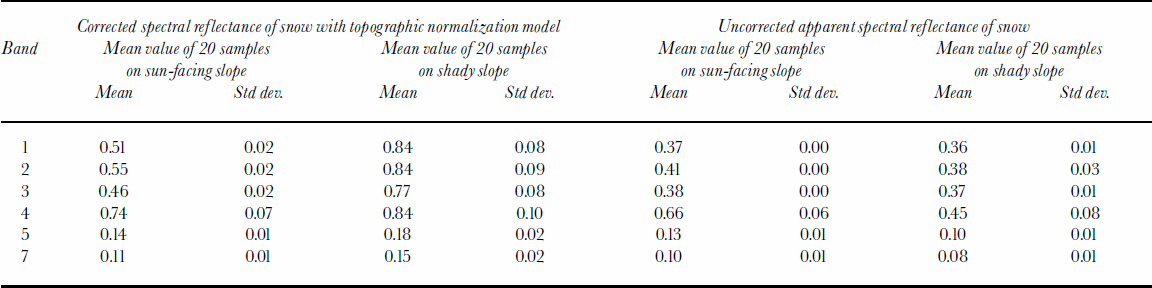
The observed phenomenon of data saturation when retrieving snow reflectance has also been discussed by other investigators (Dozier, 1989; Hall and others, 1990). In our results, saturation frequently occurs on the sun-facing slope in bands 1–3. The simple explanation is that the solar elevation is high in the image, and the atmospheric transmissivity in the mountainous region is also very high, so the total irradiance is extremely large. In this case, for instance, the largest value of irradiance in band 2 is 1808Wm^–2 μm^–1, but the maximum (saturated) value of measured radiance cannot be larger than 291Wm^–2 sr^–1 μm^–1 (NASA, 2001). Obviously, the estimated snow reflectance on the sun-facing slope in ETM+ bands 1–3 is not the true value and merely shows that saturation is a serious problem.

Conclusions And Discussions

In this paper, we developed a model to calculate the spectral reflectance of snow by normalizing the topographic effect and correcting the atmospheric effect simultaneously. The main improvement in this model was that it considers the shadowing effect of the surrounding terrain on both direct and diffuse irradiance by using the obstruction coefficient in sun-ray direction and introducing the isotropic view factor. In addition, we presented a new method to calculate the surrounding-reflected irradiance by introducing the shape factor which is defined as the ratio of the energy reaching another pixel to the energy reflected from the source pixel. A program has been developed to calculate the spectral reflectance of snow at ETM+ bands 1–5 and 7. The results from visual interpretation and statistical analysis of snow reflectance showed that many terrain effects were successfully removed by using the model. Snow reflectance reached the expected values on the shady slope. But when solar irradiance is high, saturation is a serious problem when retrieving snow reflectance.

As a deterministic method, this model has advantages in the quantitative retrieval of spectral reflectance compared to simple normalization models such as the cosine-law and Minnaert methods. We did not compare this model with other deterministic topographic normalization models. But in concept, since this model took into account the shadowing effect of surrounding terrain on both direct and diffuse irradiance and did not neglect the component of surrounding-reflected irradiance, the over-correction problem reported in other models was not found in the results presented in this paper.

The shortcoming of the model was that we used some semi-empirical methods to simulate the spatial distribution of air pressure, precipitable water and other variables that impact on the atmospheric transmissivity. However, the spatial distribution of these variables is complex, depending not only on elevation, but also on slope, slope orientation, land-cover class and other factors. The appropriate atmospheric correction depends on the correct modeling of the spatial distribution of these factors.

In addition, the model assumes that the underlying surface is a Lambertian reflector while involving the reflected radiation. Actually, snow is not Lambertian, and the reflection of the solar radiation by the underlying surface is heterogeneous, which can be described by the bidirectional reflectance distribution function (BRDF). Creative and pioneering work has been carried out by Li and Wang (1995) in these respects. Consideration of the BRDF in retrieving the spectral reflectance of snow should be a priority in future research.