1 Introduction
Nonlinear numerical sea-ice models have been successfully applied to many regions. The model developed for the Arctic Ice Dynamics Joint Experiment (AIDJEX) was used for studies in the Beaufort Sea area (Reference ColonyColony 1976, Reference PritchardPritchard 1978, Reference Pritchard, Coon and McPheePritchard and others 1977). Models have been applied to the entire Arctic (Reference HiblerHibler 1979, Reference Hibler1980) as well as to the Antarctic (Reference Hibler and AckleyHibler and Ackley 1982). In these models the sea ice is considered as a two-dimensional continuum characterized by a nonlinear plastic rheology. The dependence of the stresses used upon the strain-rates and the ice strength are determined by the choice of a yield curve. Various shapes of yield curve have been used in sea-ice models, all of them physically acceptable. However, from this broad range of possible yield curve shapes, no criterion has been formulated to determine which most realistically describes the behaviour of sea ice.
To model pack ice where it appears as a collection of floes, such as in a marginal ice zone, we consider a simple model in which the ice cover consists of a number of circular floes. Section 2 deals with some of the statistics of a distribution of finite-sized discs in two dimensions. In section 3, the kinematics of a set of randomly-distributed floes in some large-scale velocity field are considered, from which are derived dynamically important quantities such as the floe collision rate. As in previous studies (Reference Parmerter and CoonParmerter and Coon 1972, Reference RothrockRothrock 1975), the stress in the ice is associated with ridging mechanisms; however in this case we appeal to the collision model to give an estimate of the amount of ridging that occurs in various kinds of floe fields (relative to that occurring during pure compression), from which a plastic yield curve may be deduced. Because of the nature of the model, the yield curve is derived only in the limit as the ice strength tends to zero. The use of the same shape of yield curve for higher strength ice is discussed. A simple argument is presented which suggests that the same shape of yield curve may be used in the case of a continuous ice cover.
Reference SolomonSolomon (1973) describes a one-dimensional finite floe model applicable in the case where the fraction of area occupied by leads is small. Timokhov (Reference Timokhov1967[a], Reference Timokhov[b]) also considers finite-sized floes and derives equations for ice drift based on the idea of collisions between the floes caused by the stochastic variation in their velocities, but again is restricted to the one-dimensional case. Neither Solomon nor Timokhov explicitly considers the statistical properties of the spatial arrangement of floes. We consider here the more realistic ease of finite-sized floes in two dimensions and also include the possibility of low ice concentration.
2 Spatial Distribution
2.1 Ice-floe field
Some areas of sea ice, such as marginal ice zones, contain distributions of floes of various shapes and sizes. This situation is modelled here by considering an idealized floe field in which variations in floe shape are neglected, all the floes being considered circular.
A floe field, within a region R, is described by the quantities A, n and r. The compactness A is the fraction of the sea surface covered by ice, and n is the number of floes per unit area. These may be related to a third quantity r, which is the average floe radius in R, according to
Within R, the discs or floes can be considered randomly distributed in the sense that there is no preferred position for any given floe, but with the constraint that no two floe centres can be closer than 2r apart.
2.2 Distribution of circular floes
The information provided by a knowledge of the spatial distribution of a set of floes together with their velocities at some moment is sufficient to determine the instantaneous collision rate. In fact it is necessary only to consider the floes that at some time are just about to touch. We can regard the floe field as homogeneous so that we need consider only one typical floe, to which we subsequently refer as the reference floe. We take the centre of the reference floe as the origin of the coordinate system. In particular, polar coordinates (ρ, ψ) may be used so that the reference floe edge satisfies ρ = r. Also, it is found convenient to express floe velocities relative to this origin. The floe collision problem is thus reduced to determining the distribution of floes that at some moment are almost touching the reference floe. The concept of closeness of floes can be made more precise by defining a floe to be close to the reference floe if its centre lies at a distance in the range 2r to 2(r+δρ) from the origin, where δρ<<r.
For a region sparsely populated with floes, the expected number of floe centres in the annul us ρ = [2r,2(r+δρ)] is the product of its area δS and the floe number density, and is thus nδS = 8πnrδρ. This value is accurate only in the limit A → 0 since we have not restricted the possibility of floes overlapping.
If non-overlapping discs are scattered randomly then each one has about six “neighbours”, and, of course, for close-packing each disc has exactly six neighbours. From this we can find an expression for the expected number of floe centres in the annulus dS that is accurate not just for low floe densities.
The problem becomes tractable if one assumes that near the reference floe there are six floe centres uniformly distributed in the annul us defined by the range

α and β are as yet undetermined scaling constants. The constant α scales the upper limit simply because as the floe number density decreases, the floes get further apart. The constant β accounts for the finite size of the floes further out restricting the distance that the neighbouring floes can drift.
The expected number of floes with centres in the annul us ρ = [2r,2(r+δρ)] is

From the low density approximation, this expression must tend to 8πnrδρ as A → 0 which implies that α2 = 2/3. For close packing we let the upper limit in (2) tend to 2r as A → 1 which gives β = 1-α.
The expression (3) becomes
where

and δS is the area of the annulus ρ = [2r,2(r+δρ)].
This means that close to a given floe the local floe number density is L(A) times as great as the overall floe number density n.
3 Kinematics
3.1 Velocity field near a floe
Suppose that a two-dimensional ice velocity field u(x) varies on a scale much larger than the floe dimension r. If the reference floe with centre at x o has velocity u(x o) then the velocity field close by at x is

neglecting terms which are small compared to (x − x 0) · ∇u). With the centre of the reference floe as the origin, x o = 0, the relative velocity of a floe close to the origin is thus given by
Thus, close to the reference floe we consider only, linear variations in the velocity field.
3.2 Strain-rate
Horizontal variations in u are expressed by the (symmetric) strain-rate tensor

It is often found more convenient to express the strain-rate in terms of the sum and difference of the eigenvalues of
![]() . Thus we define the two strain-rate invariants
. Thus we define the two strain-rate invariants
![]() , and
, and
![]() by
by

![]() , is the divergence of the velocity field ∇ · u and
, is the divergence of the velocity field ∇ · u and
![]() is a measure of the rate of shear of the field. Sometimes another set of strain-rate invariants proves useful. These are denoted by
is a measure of the rate of shear of the field. Sometimes another set of strain-rate invariants proves useful. These are denoted by
![]() and Θ.
and Θ.

gives the amount of deformation and
![]() depends on the relative amounts of shear and divergence. If the strain-rate is specified as a point in the (
depends on the relative amounts of shear and divergence. If the strain-rate is specified as a point in the (
![]() ,
,
![]() ) plane, then
) plane, then
![]() and Θ are its polar coordinates.
and Θ are its polar coordinates.
In terms of the velocity gradients,

3.3 Collisions
We are not concerned here with the “random” collisions caused by the small-scale variation in the flow velocity field but rather the collisions due to the differential mean drift of neighbouring floes. The energy losses associated with “random” bumping of floes may be calculated in a way similar to the analysis given below for the “strain-rate” collisions. This would require additional information regarding the magnitude of the random components of the floe velocity field and is beyond the scope of this paper.
The problem then is to determine for a floe in a velocity field with strain-rate specified by
![]() and
and
![]() the resulting rate at which collisions occur with other floes. We have to determine the area within which a floe centre has to be for it to be involved in a collision in some small time δt. Expressing the relative velocity of a floe in polar coordinates (ρ,ψ), and using Equation (7), the radial velocity uρ is given by
the resulting rate at which collisions occur with other floes. We have to determine the area within which a floe centre has to be for it to be involved in a collision in some small time δt. Expressing the relative velocity of a floe in polar coordinates (ρ,ψ), and using Equation (7), the radial velocity uρ is given by

since x = ρcosψ and y = ρsinψ. Hence if we define

and

then we have

For another floe to collide with the reference floe at an angle in the range (ψ, ψ+ρψ), the radial velocity uρ has to be negative for that value of ψ, and its centre has to be within the shaded parallelogram shown in Figure 1.

Fig. 1 The shaded parallelogram contains the centres of floes about to collide with the reference floe within time St.
The total area within which a floe centre has to be to collide in a time ρt is


where ψ has been replaced by ρ' = ψ + φ/2 and the angle ψ0 is such that

Then we have
where α(Θ) =

The inverse cosine function takes its principal value. The function α(Θ) increases monotonically from 0 to 1 as Θ varies from 0 to π
The number of collisions in time δt is the product of
![]() and the local floe number density L(A)n. Thus the collision rate is
and the local floe number density L(A)n. Thus the collision rate is
For a unit area containing n floes, the collision rate is thus

where a factor of 2 in Equation (21) is lost because each collision involves two floes.
Equations (21) and (22) are, in principle, experimentally verifiable. Also they are a convenient starting point for describing several aspects of floe behaviour. For instance, their dependence upon A may in conjunction with ice-thickness distribution theory give some insight into the effect of open water upon ice strength. This line of enquiry is not followed in this paper since the only part of the ice-thickness distribution included in the description here is the fraction of open water. Instead we will concentrate on the factor α(Θ) which gives information regarding the dependence of the ice rheology upon the floe velocity field.
4 Dynamics
4.1 A yield curve
Stresses in a material can be calculated by considering the energy losses associated with the physical processes that accompany deformation. If the energy loss during some process depends on the amount of deformation but not on the rate at which the deformation occurs, then the resulting stresses are independent of the magnitude of the strain-rate. A material with this property is described as plastic.
Ice ridging is a small-scale physical process that occurs during large-scale deformation of pack ice. Assume, such as in Reference RothrockRothrock’s (1975) ridge model that the energy required to form a ridge depends on its potential energy and the work done against frictional forces during its production. The amount of energy thus needed is independent of the rate at which the ridge is built, supporting the plastic hypothesis for pack ice.
Hibler (Reference Hibler1979, Reference Hibler1980) has successfully modelled a number of features of the velocity field and thickness distribution in the Arctic using a viscous plastic rheology to specify the internal ice stresses. He uses viscosities that have a nonlinear dependence on strain-rate. In this section we aim to derive a plastic yield curve from which the viscosities can be obtained and used in a sea-ice model of this kind.
In a two-dimensional ice field, the stress state can be represented by the stress tensor with components σij which have dimensions of force per unit length. Stress invariants
![]() , and
, and
![]() can be defined in a way similar to the strain-rate invariants
can be defined in a way similar to the strain-rate invariants
![]() , and
, and
![]() . Thus
. Thus


where −
![]() is the pressure component of the ice stress and
is the pressure component of the ice stress and
![]() is a measure of the shear stress. In Reference HiblerHibler’s (1979) model, the stress σij is related to the strain-rate
is a measure of the shear stress. In Reference HiblerHibler’s (1979) model, the stress σij is related to the strain-rate
![]() by a constitutive equation of the form
by a constitutive equation of the form

where η and ζ are the shear and bulk viscosities and p* is a pressure or ice-strength term.
For a two-dimensional plastic medium a yield function F(
![]() ,
,
![]() ) can be defined such that no strain occurs for values of σ with F < 0 and that the medium yields when F = 0. The curve in the (
) can be defined such that no strain occurs for values of σ with F < 0 and that the medium yields when F = 0. The curve in the (
![]() ,
,
![]() ) plane defined by F(σ) = 0 is known as a yield curve. Clearly the origin σ = 0 will lie on or within the yield curve.
) plane defined by F(σ) = 0 is known as a yield curve. Clearly the origin σ = 0 will lie on or within the yield curve.
Reference RothrockRothrock (1975) shows how a knowledge of the amount of ridging, specified by a coefficient αr(Θ), in an arbitrary deformation can be related to the yield function and yield curve of plasticity theory. He equates the rate of working
![]() in deforming the material to rates of production of potential energy and the loss of energy in frictional processes. The energy equation he derives expressed in terms of the stress and strain-rate invariants is
in deforming the material to rates of production of potential energy and the loss of energy in frictional processes. The energy equation he derives expressed in terms of the stress and strain-rate invariants is

where p* is the strength of the material in pure compression.
The collision rate given by Equation (22) is a product of kinematic variables
![]() and αr(Θ) and variables associated with the physical structure of the floe field A, n and r. We assume that ice ridges are produced as a result of collisions and that the rate of production of ridges, and hence the rate of loss of energy, is proportional to
and αr(Θ) and variables associated with the physical structure of the floe field A, n and r. We assume that ice ridges are produced as a result of collisions and that the rate of production of ridges, and hence the rate of loss of energy, is proportional to
![]() α(Θ), which is the kinematic factor in Equation (22). Thus
α(Θ), which is the kinematic factor in Equation (22). Thus

The ridging coefficient αr(Θ) used by Reference RothrockRothrock (1975) in Equation (26) is normalized so that αr(π) = 1. The quantity α(Θ) is likewise normalized so by comparing Equations (27) and (26), we can write
Equating α(Θ) and αr(Θ) is the simplest possible assumption we can make about these functions. There are many points that should be included when making a fuller study of ice interaction. Firstly, this model has no incorporation of ice-thickness distribution except that the amount of open water is specified. Thus we cannot properly include ridging. The occurrence of collisions gives information regarding the initiation of a ridge but not its subsequent development. In particular, in this model, less ridging will occur as a result of glancing collisions because of the smaller area in which a floe has to be for it to collide, but no account is taken of smaller ridges being produced as a result, requiring less energy. The derivation of α(Θ) is based on a model of the pack that is most applicable in the case where there is enough open water present to reduce the ice strength significantly, that is, to reduce its resistance to pure compression. Thus, in fact, we are dealing with the case in which there is very little ice-ridge formation. The importance of α(Θ) is that it gives an indication of relative amounts of ridging for the various types of flow, even though the amount of ridging is small. It is α(Θ) that will be used to give the shape of a plastic yield curve whereas its size, which depends on the ice strength, is not determined by this model. The function αr(Θ), in the case where there is no open water and the ice strength is high, cannot be deduced from a collision model. However, suppose that, in such a case, a continuous ice cover is deforming with uniform spatial gradients. Suppose also that the ice cannot support tension so that open water is produced by divergence with no loss of energy. Then the loss of area of ice due to ridging from a circular region 2r in diameter is given by Equation (16). Thus the rate of loss of area due to ridging per unit area (which defines
![]() αr(Θ)) is
αr(Θ)) is
![]() α(Θ). Hence αr(Θ) = α(Θ). Subsequently, α(Θ) refers to the ridging amount for weak ice in which there is a significant amount of open water, and also to that for a continuous ice cover. The intermediate cases, such as when the ice cover consists of highly compacted floes, require further study.
α(Θ). Hence αr(Θ) = α(Θ). Subsequently, α(Θ) refers to the ridging amount for weak ice in which there is a significant amount of open water, and also to that for a continuous ice cover. The intermediate cases, such as when the ice cover consists of highly compacted floes, require further study.
By considering general properties of plastic materials, Reference DruckerDrucker (1950) derived the normal flow rule, which specifies that for a stress on the yield curve, Θ is equal to the angle between the normal to the yield curve at that point and the s, axis, and can be written in the form

The normal flow rule states nothing about the magnitude of
![]() only its direction with respect to the
only its direction with respect to the
![]() , and
, and
![]() axes. Hence is λ just a constant that remains undetermined.
axes. Hence is λ just a constant that remains undetermined.
The energy Equation (28) can be written (Reference RothrockRothrock 1975)

where α(Θ) is given by Equation (17) and the normal flow rule is expressed in the form
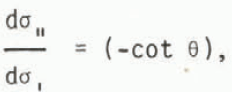
where
![]() has been regarded as a function of
has been regarded as a function of
![]() .
.
Equation (30) defines a family of straight lines in the (
![]() ,
,
![]() ) plane with the parameter Θ. The envelope of this family of lines satisfies Equation (31) and is thus the yield curve. For 0 < ? < ¼ π the lines all pass through the origin and for ¾ π < Θ < π they all pass through the point (−p*,0). For ¼ π < Θ < ¾ π, Θ can be eliminated from Equations (31) and (30) to give
) plane with the parameter Θ. The envelope of this family of lines satisfies Equation (31) and is thus the yield curve. For 0 < ? < ¼ π the lines all pass through the origin and for ¾ π < Θ < π they all pass through the point (−p*,0). For ¼ π < Θ < ¾ π, Θ can be eliminated from Equations (31) and (30) to give

Since the yield curve is the envelope of the straight line solutions of Equation (30) we require the singular solution of the differential Equation (32) which is

The full yield curve is symmetric about the
![]() axis and is thus as shown in Figure 2.
axis and is thus as shown in Figure 2.

Fig. 2 The derived sine-wave lens yield curve.
The pointed ends of the yield curve indicate that a range of values of Θ rather than a single value give rise to a particular stress. For ¼ π < Θ < ¾ π, using the flow rule in the form of Equation (29) to obtain

and
λ can be eliminated to give

The minus sign occurs so that the inverse cosine function can take its principal value. From Equations (33) and (36) we obtain

Figure 3 shows the stresses
![]() and
and
![]() as functions of Θ. The dashed curves are the results obtained from Reference HiblerHibler’s (1979) elliptical yield curve with eccentricity, e = 2.
as functions of Θ. The dashed curves are the results obtained from Reference HiblerHibler’s (1979) elliptical yield curve with eccentricity, e = 2.

Fig. 3 Stresses
![]() and
and
![]() in terms of Θ. Stresses derived from Hibler’s yield curve are the dashed curves.
in terms of Θ. Stresses derived from Hibler’s yield curve are the dashed curves.
The similarities in the stress curves between those derived from the sine-wave yield curve and Hibler’s elliptical yield curve, reflect the similarities in the shapes of the yield curves themselves. Both are closed convex curves passing through the origin and the point (−p*,0).
For the sine-wave yield curve, zero stress occurs for Θ < ¼ π for which
![]() >
>
![]() . In this state no collisions occur and leads of all orientations within the pack ice open up. As long as the convergence is larger than the shear, then the actual value of the shear has no effect on the ice rheology, and, similarly, if the divergence is larger than the shear, then the pack ice is essentially drifting freely and the ice interaction is zero.
. In this state no collisions occur and leads of all orientations within the pack ice open up. As long as the convergence is larger than the shear, then the actual value of the shear has no effect on the ice rheology, and, similarly, if the divergence is larger than the shear, then the pack ice is essentially drifting freely and the ice interaction is zero.
5 Conclusions
It is possible to derive results concerning the dynamics of sea ice, when it is composed of floes, by considering a simply physical model. The expression derived for floe collision rate can he tested experimentally. The idea of a floe field made up of a random distribution of circular floes can be exploited to produce useful results. In particular, the derived yield curve may easily be employed in existing sea-ice climate models.
The choice of yield curve in climate models has in the past been a matter of intuition. Any shape of yield curve that is physically reasonable has been acceptable. The derivation of a particular yield curve, a sine wave lens, to describe the plastic behaviour of certain categories of sea ice puts the process of choosing such yield curves on more of a sound footing.
I would like to thank P Wadhams and W D Hibler III for helpful comments during the writing of this paper.
The work was done during a Co-operative Awards in Sciences of the Environment (CASE) studentship funded by the Natural Environment Research Council in association with the Meteorological Office, Bracknell.





