Sea Ice Budget Studies of Baffin Bay Using A Numerical Ice Model

Abstract

The dynamic-thermodynamic model of sea ice due to Hibler (1979) has been adapted for simulations of the Baffin Bay pack. The simulations were carried out for wind fields characteristic of the more common synoptic situations for July, the ice conditions of July 1969 being taken as typical of this month to initialize the model. Average long-term currents were also used. The modelled ice characteristics were consistent with expected results for the forcing fields and rheology of the ice. A comparison of advectional ice losses through Davis Strait with the melt in situ shows the melt to be an order of magnitude larger. However, the melt alone cannot clear the ice out of Baffin Bay. It seems that the mechanism for this process involves a slow consistent melt coupled with a short period of northwesterly winds.

1 Introduction

Baffin Bay is the body of water which extends from the Arctic Circle to 78°N and from Baffin Island to Greenland. It has several small sounds westward and northward to the Arctic Ocean and a large strait, Davis Strait, southward to the Labrador Sea. In terms of the overall ice budget for the area, the influx of sea ice into Baffin Bay from these sounds is small compared to the amount produced by freezing, especially for a July simulation. On the other hand, there probably are situations during break-up or certain synoptic times when there is a more significant contribution. These events are not considered here.

The ice either leaves the area through Davis Strait or melts in situ. The situation is somewhat analogous to the behaviour of the pack in the Arctic Ocean, but at different temporal and spatial scales.

The behaviour of the pack in Baffin Bay has been of interest since the time of the Vikings, but recent interest has been associated with resource development, both in the area and connected with the transportation needs of development in the high Arctic. This sequence of man’s activities has both generated and used a great deal of sea-ice information. In recent years satellite imagery has been used for icedrift speeds (for instance, see Dey 1978) and for the compilation of sea-ice atlases for the area (Lindsay 1977, I to 1982). A significant data set also exists 1n the maps of ice conditions produced by the Canadian Ice Central in Ottawa. While the sea-ice data may not be available in the best format for numerical modelling, there is a sufficient database for the initialization and validation of a numerical model.

The situation is similar for the climatological aspects of Baffin Bay as it relates to the ice, for instance see Jacobs and others (1974), Crane (1978), and Jacobs and Newell (1979). Analysis of surface weather conditions are also available on weather maps produced by the Canadian Atmospheric Environment Service, This is an adequate source of wind data for ice modelling.

The other input data needed for ice modelling are the ocean currents. There are few observations of currents for this area, and the best available are long-term average estimates.

A number of areas of study could make use of the results of a numerical model. These include forecasting of ice movement in relation to shipping, or in historical studies relative to Arctic exploration and whaling operations. Here we concentrate on estimating the mass balance of the ice between melt in situ and advection through Davis Strait for a July period for a number of synoptic situations. This is a straightforward goal for test simulations to verify that the model is operating correctly, to assess the relative importance of the two sinks of ice, and to obtain some idea of the mass flux into the Labrador Sea from Baffin Bay. This last estimate 1s important input data for the on-going modelling effort for the Labrador Sea pack (Keliher and Foley 1983).

The numerical model used in this study was adapted from that of Hibler (1979) with several modifications as noted by Tucker (1982). It was applied for a model area extending from Baffin Bay to the northern part of the Labrador Sea. Ice extents, concentrations, and velocities were simulated for some typical synoptic situations taken from Barry and Keen (1978). Mass fluxes for melt and advection were calculated for the most common synoptic types for the month of July. In general the melting losses were one order of magnitude larger than the advective losses.

2 Model Description and Application

The model adapted for use was the two-thickness level, viscous-plastic model developed by Hibler (1979) of which the original code was also provided by Hibler. The code and documentation are also available in Hibler (1980). It has been used for a number of simulations in the Arctic Ocean (Hibler 1979) and more recently for the East Greenland Sea (Tucker 1982). The application for the East Greenland Sea is quite similar to that discussed here and the following summary of the model relies heavily on Tucker (1982). More detailed discussions are available in Hibler (1979, 1980). The model uses a momen-tum balance equation of the form

where d/dt is the total time derivative (∂/∂t) +

.R, m is the ice mass per unit area,

is the two-dimensional ice velocity, f is the Coriolis parameter,

is a unit vector normal to the sea surface,

and

are the air and water stresses respectively, H is the sea-surface dynamic height, g is the acceleration due to gravity, and

the internal ice-stress term. The air and water stresses are specified as a quadratic function of the difference between the ice velocity and either the geostrophic wind or current velocities with a turning angle. In actual practice the ice velocity is usually neglected with respect to the geostrophic wind velocity. For low wind speeds this assumption can lead to appreciable errors; however, for these cases the water stress is the much larger term, so the effect on the simulations should be small.

The form

depends on the assumptions of the constitutive law for ice. This has the structure of a non-linear viscous compressible fluid, written by Hibler (1979) as

where σ_ij is the two dimensional stress tensor,

is the strain-rate tensor, P/2 is a pressure term, and ζ and η are nonlinear bulk and shear viscosities. The internal stress components are calculated from

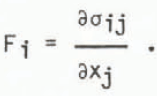
The values of η and ζ, which depend on and P, are taken so that the stress state lies on an elliptical yield curve passing through the origin. This specification gives rigid plastic flow. For very small strain-rates the viscosities become very large, and to overcome this difficulty they are constrained to be less than a maximum value. Thus, for small strain-rates, the constitutive law is linear-viscous.

The specification of P 1s related to the two-layer approach to the ice-thickness distribution. While Thorndike and others (1975) have provided a rigorous distribution theory, it was not used here because of its complexity. Instead, each grid square is considered to be covered by ice of average thickness h and compactness A. In defining h and A, only thicknesses greater than 0.5 m are used. Ice thicknesses less than this are considered to be open water. The thickness and compactness obey the continuity relations

S_h and S_A are the thermodynamic terms which produce the ice thickness and compactness as a function of 1ce growth and decay. Since a July simulation was considered here, the ice-growth rates for the middle of July from Coon and others (1974) were used. At that time of year the 1ce is melting for all thicknesses at rates ranging from −0.0110 to −0.0155 m d⁻¹. The rates are not strongly dependent on time for that period so no temporal variation was included in the simulations. In addition no spatial variation was included. These rates do not include the effect of increased solar absorption in leads. An estimate of this error is discussed later. The diffusion terms give numerical stability.

In terms of h and A the quantity P is parameterized as

P = P*h exp[−C1-A)].

P* and C are empirical constants. P* is the major parameter of the model. For the looser ice conditions of the East Greenland Sea, Tucker (1982) found that it was necessary to use a value of 2 x 10⁴ N m² which is four times larger than the original modelling in Hibler (1979). It was felt that the sea ice of Baffin Bay was more like that of the East Greenland Sea than that of the Arctic Ocean, so Tucker’s value was used. It was not necessary to change the value of C of 20 (Hibler 1979).

The wind data were based upon the six most common synoptic types in July for Baffin Bay (Barry and Keen 1978). The actual isobar spacing was not given, and the table below gives our wind estimates along with other synoptic information.

For each simulation wind speed and direction were taken to be uniform over the model area and constant for a one-week period.

The currents were long-term estimates taken from Dunbar (1951) and are shown in Figure 1.

Fig. 1 The current field, after Dunbar (1951), as used for input for the simulations. For clarity not all data are shown.

The ice data in Figure 2 were taken from the map in Canadian Meteorological Service ¢1971) for July 1969 and represent a typical July period. The ice depths were difficult to estimate from the data on the map. At best they were a crude estimate based on the concentration and types of ice and some personal judgment (J Newell private communication). The ice was generally packed in against Baffin Island, and, with the generally light winds, not much drift would be expected in the simulations.

Fig. 2 The ice data, after Canadian Meteorological Service (1971), used to initialize the simulations.

The model area is shown in Figure 3. It is a subgrid of the grid of the Canadian Meteorological Service, which in itself is a portion of a grid used by the US Navy Fleet Numeric Facility. The equidimensional grid is based upon a polar stereographic map projection. The grid spacing was 38.3 km. Also indicated is the line taken to represent Davis Strait; ice reaching this limit was considered to have left Baffin Bay.

Fig. 3 The model area for Baffin Bay with the grid points.

The finite difference scheme used to solve the coupled equations was based upon a staggered grid procedure. The momentum equation was solved by a semi-implicit predictor-corrector over-relaxation scheme. The velocities were calculated at the grid points. The thickness and compactness equations were calculated for each grid cell. The model time-step for the computations was taken as 6 h (Tucker 1982).

3 Results and Discussions

Simulations were carried out for six different wind regimes for ice conditions and melt rates characteristic of July. Figures 4 and 5 present the compactness and velocities at the end of one model week for synoptic types 1 and 5 of Table I. These two cases generally represent the extremes of the synoptic situations studied. Figure 4 shows that the effect of the northeasterly wind is to pack the ice against Baffin Island with an increased compactness. Correspondingly the ice has moved away from the Greenland side. With the southerly wind of type 5 the ice has covered much of the bay with a lower compactness but with a greater compactness in Melville Bay. In both cases there is an area of low compactness in the central portion of the pack due to the divergent currents associated with a gyre in the northern part of the bay (Fig.1). This forces strong advection of ice out of the area of low compactness. In the Davis Strait area the two wind regimes lead to different behaviour. The northeasterly winds force the ice towards the shore, but the currents are sufficient to advect ice out of the area. However in the case of the southerly winds, the currents are not strong enough to overcome the air stress and ice moves north-ward.

Fig. 4 The ice compactness at the end of a one-week simulation period for synoptic types 1 and 5. The direction of the geostrophic wind is shown in the upper right-hand portion of the figure.

Fig. 5 The ice velocities at the end of a one-week simulation period for synoptic types 1 and 5. The direction of the geostrophic wind is shown in the upper right-hand portion of the figure. For clarity, not all data are shown.

Table I Summary of the Characteristics of the Most Common July Synoptic Types for Baffin Bay

The contours of ice thicknesses are quite similar to those of the concentration, so no graphical results are presented here. Generally where the compactness increased, the thickness increased. In areas where the compactness decreased, the thickness decreased slightly, due not to dynamic effects but to melt. For the case of the northeasterly winds the simulated thicknesses increased to a maximum of about 2.4 m along Baffin Island except near the shore where the original 3 m ice decreased in thickness due to melt. In the other synoptic cases the greatest thicknesses, with a maximum of 2.5 m, were obtained in a thin strip along the coast of Greenland. In the low compactness area in the centre of the grid, the thicknesses were small, about 0.7 m for the case of type 1 and 0.2 m for type 5.

The ice velocities are displayed in Figure 5. Both synoptic cases show ice drifting south-eastward along the coast of Baffin Island, obviously due to the large southeasterly currents. However, in a thin strip near the coast, the velocities are reduced because of compact thick ice. Away from the coast the effect of the different wind inputs is indicated. The northeasterly type 1 winds and currents move the ice in a southwesterly direction in most of Wie model area except in the north and in Davis Strait, where the velocities are more southerly. The relatively large type 5 southerly winds force northward motion with appreciable velocities in central Baffin Bay. Near the Greenland coast, in the top of the model area, the velocities decreased due to the ice packing into a high compactness strip. The large ice velocities further down the Greenland coast seemed to be due to three factors: first, the wind and water stresses were acting in the same direction providing a large external force on the ice; second, these stresses were forcing the ice into an open-water area where the internal ice stress cannot act to reduce velocities; and third, the ice concentrations and thicknesses were small 1n these areas, thus providing a small ice mass to be acted upon by these stresses. There is also a possibility that the relatively large ice forcing and low ice mass leads to some sort of numerical instability. The reason for this is not clear, but other work in progress on the application of this model to the Labrador Sea has occasionally simulated ice velocities that are higher than expected in similar ice conditions. In Davis Strait there was a slow northward drift where the southerly wind stress is slightly larger than the southward water stress.

Further results of this modelling are given in Figure 6. The total mass rates for melt and advective loss are shown for the six synoptic types. The ice melt for each synoptic type was calculated but there was so little difference between each type that only one curve is displayed. The general decrease of the melt rate arises because the total amount of ice is decreased due to melt and advection. As already demonstrated, the advection out of Davis Strait depends on the synoptic type, and the advective losses are shown in the lower part of the figure. The k ink during the first model day is a spin-up effect because initial ice velocities are zero. After that the advective loss slowly decreases for the same reasons as the decrease of the melt. The curve for type 5 shows the northward advection feature (ice gain). It is approaching zero because the amount of ice available for northward movement is decreasing rapidly.

Fig. 6 The top portion shows the amount of ice melt for the one-week simulation period. The bottom portion shows the amount of ice being advected out through Davis Strait for the six synoptic types simulated.

While the currents are probably large enough to give appreciable advection of ice, the wind fields of the various synoptic types tend to trap ice against the coast. With favourable northwesterly winds the situation could be quite different. The fact that the spin-up time of the model is about a day indicates that large advection rates could be expected to develop in that time scale, given favourable winds. However these winds are not very common (Barry and Keen 1978).

The average thickness of ice in Baffin Bay was estimated to be about 1.8 m and the melt rate about 0.015 m d⁻¹ (Coon and others 1974). Thermodynamics alone would thus require about three months to melt all the ice. This melt rate is for a solid ice cover, and it may be too small for the more open conditions in Baffin Bay, where increased solar radiation absorption by the open water will increase the melt rate by approximately the ratio of the albedo of melt-pond covered ice to open water, i.e. by a factor of 2 or 3. The average compactness of the ice-covered portion of the bay is about 0.75, so in 25% of the area the melt rate is some three times as large as the other 75%. The actual melt rate is about 50% larger than the value used for the simulations. The values in Figure 6 could be as much as 75 x 10⁶ kg s⁻¹ and the clearing could take place in two months. Thus it would still seem that the general mechanism for clearing Baffin Bay would have to be that the melt slowly reduces the quantity of ice, followed by a short period of favourable winds which finally clears the bay.

Satellite data have the potential to confirm the simulated advectional losses, although they cannot be used now as observed winds and currents were not used in this simulation. Estimates based on imagery would provide a useful verification and in further simulations it would be valuable to select periods where advectional losses are known or could be estimated.

There are a number of assumptions made here which could change these results. As just noted, the melt rate is probably a low estimate. It, as well as possible growth, depends on the temperature and cloudiness of the air mass being moved over the water and hence on the synoptic situation. Larger melt rates would also be due to the high sun angle and strong solar absorption of open water. The wind field has been taken as constant in space and time, and while persistent winds might occur at this time of year, it is certainly true that the winds will vary over the model area. Further modelling efforts will attempt to include this variation.

4 Conclusion

The results presented here indicate that the numerical ice model used provided good simulations of the behaviour of the pack in Baffin Bay. The ice velocities were consistent with the wind and current fields while the rheological specification decreased the velocities in areas of thick compact ice near the coasts. Advectional losses through Davis Strait were an order of magnitude lower than the melt losses for the selected synoptic types, which make up about 50% of the weather patterns characteristic of a July month. The mechanism for the clearing of ice out of Baffin Bay for this month would seem to be the slow consistent melt of ice coupled with the development of a short period of northwesterly winds.

The major problems with the simulations are due to the lack of good input data, though the satellite imagery is capable of providing extensive ice data. The other difficulty is the use of ice-melt rates typical of a totally ice-covered sea rather than a partially open sea. Increased solar radiation absorption in the open water portions of the ice cover could increase the total melt in Baffin Bay by 50%.