1. Introduction
The recently drilled deep ice cores GRIP (Greenland Ice Core Project), GISP2 (Greenland Ice Sheet Project) and Vostok (in East Antarctica), which reach back more than 200 ka and thus cover two full Glaciol/intcrglaciol cycles, have considerably improved our knowledge of the palaeocli-mate. in order to supplement the information from these ice cores with further data and find answers to still open questions (such as those concerning the occurrence of rapid climate variations in the Eemian and the coupling of climate changes between the Northern and Southern Hemispheres), several further ice-core projects in Antarctica are planned, an international effort coordinated by the Scientific Committee on Antarctic Research. Europe's contribution to this campaign is the European Project for Ice Coring in Antarctica (EPICA), an outcome of the work of the European Committee on Ocean and Polar Sciences. Within this programme, it is planned that two deep ice cores will be drilled in Antarctica, one at Dome Concordia (central East Antarctica) and one in Dronning Maud Land (Atlantic sector of East Antarctica; sec Fig. 1).The former is expected to provide an archive which covers more than 500 ka of climate history, while the latter, to be drilled in a region influenced by precipitation sources from the South Atlantic and with relatively large accumulation rates, concentrates on rapid climate changes in the most recent Glaciol/intcrglaciol cycle (Reference Jouzel, Hammer, Miller, Orombelli, Peel and StauffcrJouzel and others, 1994).
In this study, we present a preliminary simulation with the three-dimensional polythermal ice-sheet model SICOPOLIS (Simulation Code for Polythermal Ice Sheets) fot-the Antarctic ice sheet in order to offer model support for the ice core in Dronning Maud Land. During the planning phase, the simulation results are helpful in determining the optimum drill-site. Besides a large accumulation rate necessary to obta in the desired high temporal resolution of the climate archive, criteria for this are (i) the thermal conditions at the bedrock (avoiding basal ice at pressure melting), (ii) the age of near-basal ice, and (iii) from an engineering point of view, the shear rate in the borehole. During the actual drilling process, the age-depth profile of the ice core must be computed by flow modelling in the deeper regions where stratigraphie techniques are not feasible. Further, flow modelling is required to find the geographic origin of the ice in the core.This must be done with as much sophistication as possible to obtain optimum results, and should therefore not be done by simple steady-state flowline modelling.
2. Ice-Sheet Model Sicopolis
SICOPOLIS is a three-dimensional dynamic/thermody-namic ice-sheet model based on the continuum-mechanical theory of polythermal ice masses (Reference Fowler and LarsonFowler and Larson, 1978; Hinter, 1982,1993; Calov and Hutter, 1997; Greve, 1997b). It simulates the time-dependent extent, thickness, velocity, temperature, water content and age for a grounded ice sheet in response to external forcing. Further, possible basal layers of temperate ice are detected with high vertical resolution by fulfilling the Stefan-type conditions at the cold-temperate transition surface. External forcing is specified by (i) mean annual air temperature above the ice, (ii) surface mass balance (accumulation, surface melting), (iii) sea level surrounding the ice sheet, and (iv) geothcrmal heat flux from below. The dynamics of the adjacent ice shelves is not accounted for. The model is discussed in detail by Greve (1995,1997a) and Hansen and Greve (1996).
Fig. 1. (a) Measured surface topography of the present Antarctic ice sheet, by Reference DrewryDrewry (1983). Ice shelves are ignored. The shaded area marks the region in Dronning Maud Land where the EPICA core will be drilled (Jouzel and others, 1994). Surface elevations in km a.s.l. (contour spacing 500 m). (b) Close-up of the coring region in Dronning Maud Land (contour spacing 250 m).
In this study, SICOPOLIS is applied to the Antarctic ice sheet. The results of a transient palaeoclimatic simulation which covers two entire Glaciol/inlerglaciol cycles are presented, with special emphasis on Dronning Maud Land. Horizontal grid spacing is 109 km. The vertical resolution is 51 gridpoints in the cold-ice region (temperature below pressure melting), 11 gridpoints in the temperate-ice region (temperature at pressure melting) if existing, and 11 grid-points in the lithosphere.
3. Simulated Present State of Dronning Maud Land
3.1. Model set-up
In order to provide an optimum present state of the Antarctic ice sheet and avoid prescribing lateral boundary conditions, a transient palaeoclimatic simulation was carried out for the ice sheet as a whole. This simulation covers 242200 years of climate history (two climatic cycles), parameterised by the temperature reconstruction 
of the Vostok ice core (Jouzel and others, 1993,1996) and the SPECMAPsea-level record zai(t) (Reference Imbrie, Berger, Imbrie, Hays, Kukla and SaltzmanImbrie and others, 1984). It was initialised by a previous 100 000 year steady-state run forced by the climate conditions at 242 200 BP. in this initialisation run, the lithosphere temperature was assumed to be in equilibrium with the geothermal heat flux from below and the temperature at the ice base at any time in order to reach the steady state within 100 000 years.
It is assumed that the spatial distributions of the mean annual and summer air temperature above the ice, Tma and Tsu, respectively, remain unchanged through time, so that
Here, 
and 
are the present distributions of the mean annual and summer air temperature above the ice, respectively, for which the parameterisations by Reference HuybrechtsHuybrechts (1993) are applied, x, y, z are Cartesian coordinates: x, y span the horizontal plane; z points upward.
For the present accumulation rate, Stoday, we made up a new map, which is based on 45 data points by Reference NeethlingNeethling (1970), Reference Picciotto, de Breuck and CrozazPicciotto and others (1970), Reference Isaksson and Karl'nIsaksson and Karlen (1994) , Reference Mulvaney and WolffMulvaney and Wolff (1994), Reference PatersonPaterson (1994) and Reference Isaksson, Karlén, Gundestrup, Mayewski, Whitlow and IwicklerIsaksson and others (1996) around the coring region in Dronning Maud Land (see figs 2 and 3). Under climatic conditions different from today's, a linear relationship between the accumulation rate S and the temperature deviation ΔΤma, is assumed:
Fig. 2. Positions of accumulation measurements in the vicinity of the coring region in Dronning Maud Land (the latter is situated with in the dashed rectangle), on which the accumulation map usedfor the simulation is based. Nos. 75-90 by Mulvaney and Wolff (1994); nos. 99-106 by Isaksson and Karlen (1994); no. 107 by Isaksson and others (1996); nos. 163-192 by Picciotto and others (1970); nos. 221-222 by Paterson (1994); no. 239 by Neethling (1970). Contours are surface elevations in km a.s.l.
Fig. 3. Interpolated accumulation pattern resulting from the measurements of 2ur for the coring region in Dronning Maud Land (in cm ice equivalent a−1). The proposed drill-site is marked by the full triangle.
The parameter 
is chosen such that the accumulation rate is reduced by 50% for the lowest temperature of the Vostok reconstruction, 
.
Surface melting is parameterised by the degree-day approach with the degree-day factors 
and 
, the firn saturation rate Pmax = 60% and the standard deviation 
for statistical air-temperature fluctuations (Reelt, 1991). The geothermal heat flux is 
(Huybrechts, 1993). The bedrock topography is by Drewry (1983). Further physical parameters are the same as those applied by Greve and others (in press), except for the enhancement factor in Glen's flow law, for which the spatially and temporally uniform value E = 5 is used here.
Fig. 4. Simulated surface topography of the coring region in Dronning Aland Land. Surface elevations in km a.s.l. (contour spacing 250 m). The proposed drill-site is marked by the full triangle.
3.2. Results
We now discuss the results of the simulation described above for the present state of the coring region in Dronning Maud Land (1. Figures 4-7 depict the computed surface elevation, h, homologous basal temperature, 
(that is, corrected for the pressure-melting point), age at 85% depth, A
85, and basal shear deformation, Sh, respectively.
Comparison of Figures 1b and 4 shows that the simulated surface topography is in reasonable agreement with the measured one. The most conspicuous discrepancy concerns the surface gradient (and therefore the flow direction) in the southeast of the depicted region where the modelled and measured directions differ by 55°. This demonstrates the preliminary nature of the results, which is due, on the one hand, to still insufficient information about the bedrock topography and the accumulation pattern and, on the other hand, to the coarse horizontal resolution and perhaps neglect of the effect of normal stress gradients on the ice flow (see below).
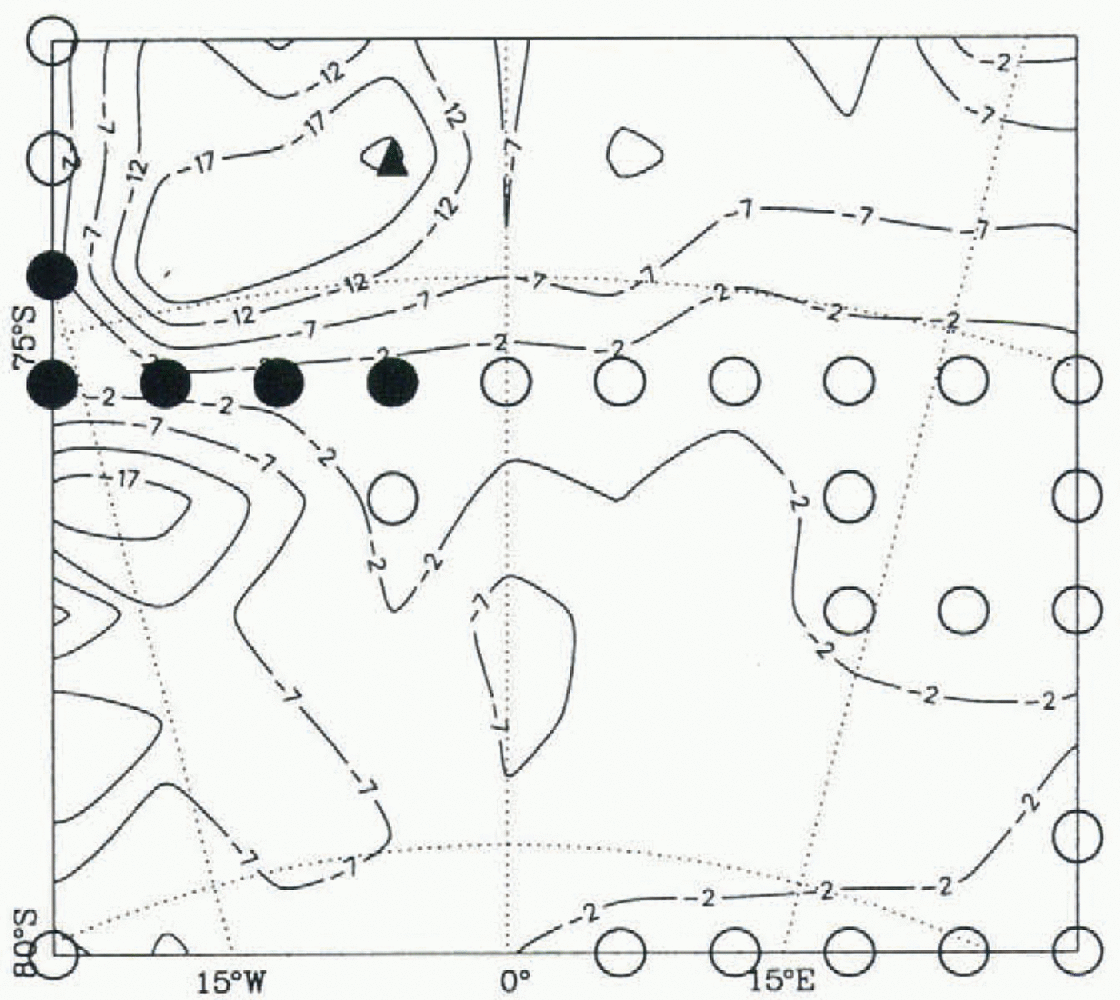
Fig. 5. Simulated basal temperatures for the coring region in Dronning Maud Land, corrected for pressure melting (in °C; spacing 5°C). Open circles (full circles) indicate gridpoints where the basal ice is at pressure melting without (with) an overlain layer of temperate ice. The proposed drill-site is marked by the full triangle.
The basal temperature shown in 5ur varies considerably, covering a range from below -20°C to pressure melting. For five gridpoints in the western part, even a basal layer of temperate ice is predicted. Since the water flow in temperate ice disturbs the stratigraphy of a potential ice core, the vicinity of these points must be avoided as coring positions.
The age at 85% depth (6 increases distinctly from northwest to southeast due to the decreasing accumulation (3 and the increasing thickness. The objective of the EPICA ice core in Dronning Maud Land is not to provide basal ice as old as possible, but to provide a climate archive with high temporal resolution for the most recent climate cycle. The lattei is certainly covered by the condition A 85 ≥ 100 ka, which excludes as possible drill-sites only positions in the northwestern corner of the region.
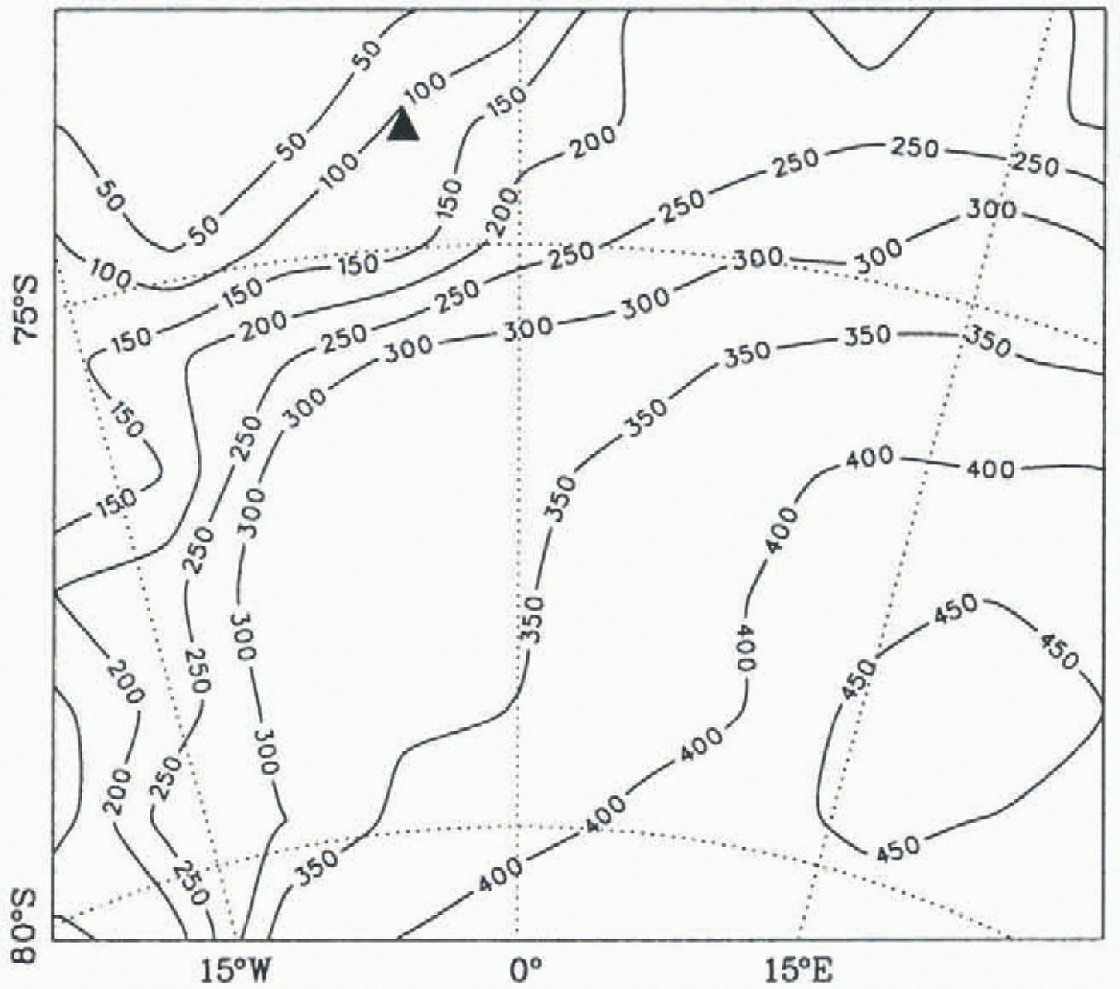
Fig. 6. Simulated age at 85% depth for the coring region in Dronning Maud Land (in ka; spacing 50 ka). The proposed drill-site is marked by the full triangle.
Numerical diffusion introduced in the age compulation, which is currently unavoidable if the numerical integration is to be kept stable, affects the computed age values most conspicuously in a near-basal boundary layer which was found to be 15% of the ice thickness for similar simulations of the Greenland ice sheet (Greve and others, in press). in the rest of the ice sheet the influence of the artificial diffusion is virtually negligible since its associated time-scale is much larger than the time-scale for the physical process of advection which governs the evolution of the age field (Greve, 1997c). As a result, we are not yet able to give a reasonable prediction for the basal age of the ice, even though the computed and depicted values for should be reliable from a numerical point of view (see the Appendix, where this is demonstrated with analytical solutions of the one-dimensional steady-state age equation with and without diffusion). Future work must consequently aim to avoid the numerical diffusion by either adopting a more stable discretisation scheme for the purely advective age equation or applying a direct particle-tracing algorithm. Such studies are on the way.
The basal shear deformation, defined by
where vx and vy are the velocities in the x and y directions, should be as small as possible at the drill-site to minimise the strain on the drill stem. 7ur demonstrates that Sh varies by more than a factor of 30 in the coring region: from below 0.01 a−1 to above 0.3 a−1. One may restrict the tolerable shear deformation to a maximum of 0.03 a−1, which confines possible drill-sites to slightly less than half of the region.
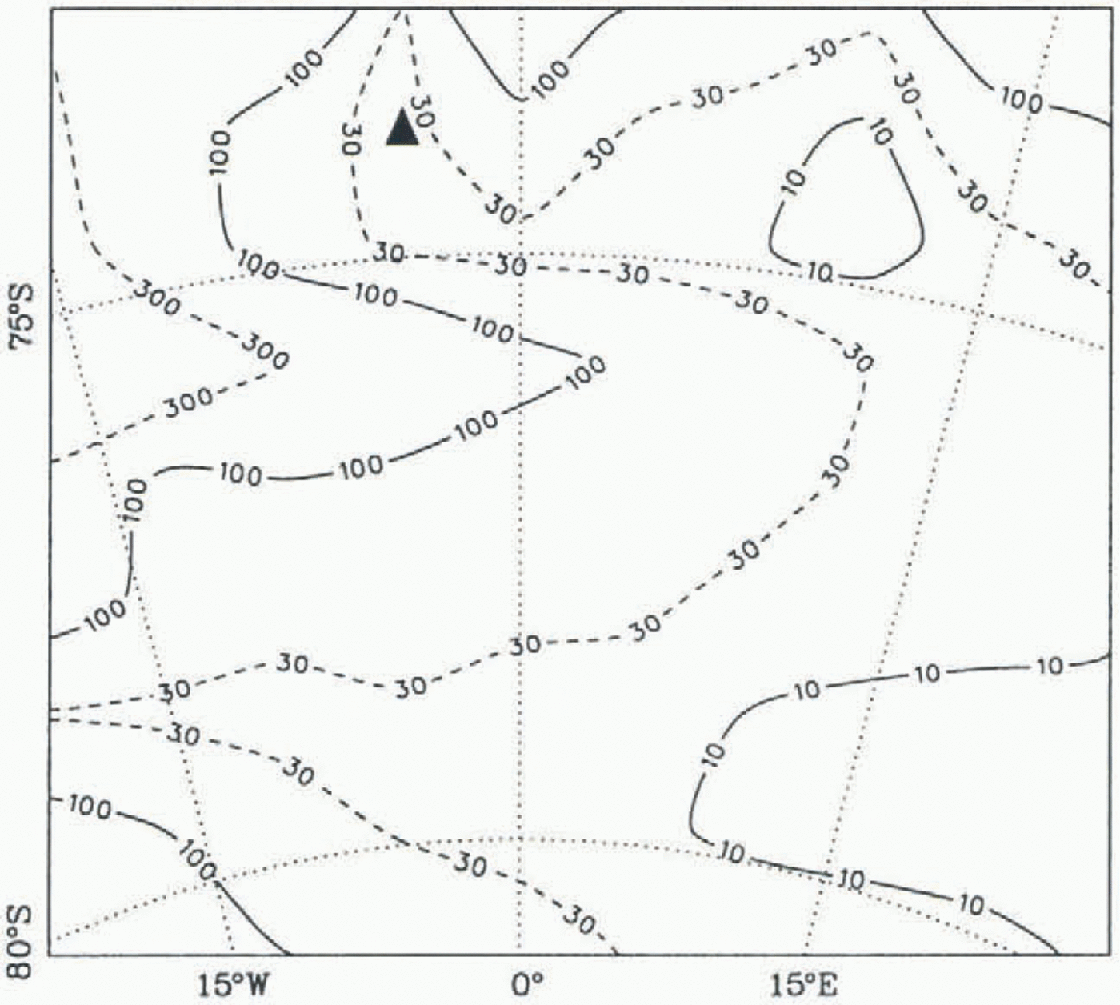
Fig. 7. Simulated basal shear deformation for the coring regie in Dronning Maud Land (in 10 −3 a −1). The proposed dril site is marked by the full triangle.
3.3. Preliminary proposal for a drill-site
With the findings of the simulation discussed above, a preliminary proposal can be made for the position of the EPICA ice core to be drilled in Dronning Maud Land. It is the gridpoint with the coordinates 73°57' S, 03°35'W, situated on a saddle in the northwest of the region considered for coring. This position is marked by the full triangles in Figures 3-7, and is characterised by the following simulated values:
Evidently, the criteria for the choice of drill-site are fulfilled very satisfactorily. The accumulation rate is sufficiently large to ensure a high temporal resolution, the basal temperature is far below melting, the most recent climate cycle is captured entirely (even though the value for the basal age is unreliable due to the disturbing effect of numerical diffusion; see above) and the basal shear deformation is small.
For further illustration, the depth profiles of the temperature, T, the age, A, the horizontal velocity, v h, and the basal shear deformation, Six, are depicted in 8ur for this position. As is typical for age-depth profiles of ice columns, the gradient is very small in the upper part where the accumulated ice layers remain essentially unchanged. By contrast, layer thinning due to ice spreading causes a distinctly larger gradient in the lower part, which explains also the big difference between the age at 85% depth and the basal age. Owing to the increase of shear stress with depth and the non-linearity of Glen's flow law, the main shear deformation takes place in the lowermost quarter of the column. Consequently, the strain on the drill stem is very small above this near-basal part.
The above results must be regarded as preliminary. The still poorly known bedrock topography and the lack of accumulation measurements in large parts of the coring region may lead to inaccuracies in the simulation results. Further measurements will be carried out in Dronning Maud Land with in the EPICA project, so that this shortcoming can be remedied in the future. Parallel to the completion of these input data, a grid refinement for the coring region in Dronning Maud Land will be implemented in our model in order to provide simulation results with higher spatial resolution. Owing to the mountain ranges of Maudheimvidda and Fimbulheimen situated downstream of the coring region, normal stress gradients which are neglected in the shallow-ice approximation on which the model is based (Greve, 1997b) may have a noticeable effect on the ice flow. Therefore, the contribution of these stress components will be accounted for in the high-resolution coring region.
Fig. 8. Simulated depth profiles of temperature, age, horizontal velocity and shear deformationfor the proposed drill-site at 73°57 S, 03°35' W.
4. Conclusion
The three-dimensional dynamic/thermodynamic ice-sheet model SICOPOLIS was applied to the Antarctic ice sheet, and the computed present state of Dronning Maud Land which results from a palaeoclimatic simulation along two climatic cycles was discussed. The objective is to provide model support for the EPICA ice core which is planned in this region. A possible drill-site is proposed based on suitable values for the accumulation rate, basal temperature, age and basal shear deformation, and a preliminary age-depth profile for this position is given.
We aim to improve the model set-up in close cooperation with the EPICA project members, who will supply new data from observations in Dronning Maud Land. in particular, a more precise bedrock topography, additional accumulation data and information on flow properties of the ice will be obtained in order to ensure a proper modelling of this region. Together with the implementation of a grid refinement and the consideration of normal stress gradients, this will lead to more accurate results which can be used to determine the final coring position. Furthermore, the computation of age depth profiles (dating) will be improved by applying a diffusion-free algorithm for the advective age equation.
Acknowledgements
We wish to thank I. Whillans, E. Venteris, H. Blatter and R. Mulvaney for supplying data on the Antarctic snow accumulation, and R. Hindmarsh, T, Jóhanncsson and A. Kerr for their helpful comments of the original draft of this paper. The support by the Deutsche Forschungsgemeinschaft under project No. Hu 412/19-2 is gratefully acknowledged.
Appendix Analytical Solution of the One-Dimensional Age Equation
Consider the one-dimensional steady-state equation for the age A,
the normalized ice-sheet geometry b= 0 (ice base), h = 1 (ice surface) and the normalized constant downward velocity 
Under these conditions, the solution of Equation (A1) is simply
Let us add some numerical diffusion to Equation (A1):
where DA is the numerical diffusivity. The solution of this modified problem is
The constant C is undefined due to the parabolic nature of Equation (A3). With the artificial Neumann-type basal-boundary condition
where ΓΑ is the prescribed basal age gradient, its value is
Table. 1. Error of the age function A (z) due to numerical diffusion. Prescribed basal gradient ΓA = 200
and thus, from Equation (A4),
With Equations (A2) and (A7), the influence of the artificial diffusion on the age function can be quantified in terms of the error
Table shows e(z) for z =0,0.01,0.15, 0.5,1, four different difiusivitics DA and the basal gradient ΓΑ = 200, which was used in the actual three-dimensional simulation discussed in this paper. Evidently, with decreasing diffusivity, the diffusion effect on the computed age concentrates more and more on a near-basal boundary layer, as was claimed in section 3.2, and, for DA < 0.01, the error is indeed negligible, down to 85% depth. With the thickness scale [H)= 2000 m, the vertical-velocity scale [V] = 0.1 m a−1 and the time-scale [T] = [H)/[V], the dimensional diffusivity 5x10 8 m −2s−1 used in the simulation corresponds to the normalised value
The numerical scheme itself is diffusion-free in the vertical because vertical advection is discretised by centred differences (instead of horizontal advection for which an upwind scheme is applied). Therefore, our assertion that the computed ages down to 85% depth are basically unaffected by the numerical diffusion is supported.
