Introduction
The ice-sheet thickness-evolution equation (where the mechanics are computed according to the shallow-ice approximation of Hutter (1983)) is of a highly non-linear diffusion-reaction type and generally needs to be solved numerically. The time steps used in the solution of this equation are limited by the requirements of stability: if the time steps are too large, then spurious oscillations are created in the ice-sheet surface. Unlike the linear diffusion equation, this does not necessarily result in blow-up because non-linear coupling of the instability prevents unbounded growth.
A number of approaches exist for the numerical solution of this equation. They can be grouped as explicit, semi-implicit (where there is no sub-time step non-linear iteration) and fully implicit (where there is full sub-time step non-linear iteration). The former two schemes are most often used in operational ice-sheet models. Their stability characteristics limit the maximum time step used in most practical applications to 1–10 years. This is considerably shorter than the natural time-scale of ice sheets and limits the number of experiments that can be made with continental ice-sheet models.
Budd and Jenssen (1976) have investigated the Stability of explicit schemes for solving the ice-sheet equations. However, since then, considerable progress has been made in the theory of iterated maps (which is what numerical solutions are), and there has been widespread adoption of semi-implicit schemes (e.g. Mahaffy, 1976; Huybrechts, 1992), and implicit or Crank–Nicholson schemes which iterate to solve the non-linear simultaneous equations using Picard or Newton–Raphson iteration (e.g. Hindmarsh and others, 1987; Hindmarsh and Hutter, 1988). All of these methods have time-step limits, which should be contrasted with the linear diffusion equation where Crank–Nicholson and implicit schemes are uniformly stable.
In this paper, we will look at the theory and practice of time-step limitations for the ice-sheet equation, First, we set out several of the more commonly used discretizations of the ice-sheet equation, We then present comparisons between these different discretizations in terms of accuracy, stability and efficiency. This is done in two idealized experiments for which analytical solutions are available: the one-dimensional case flow-law exponent (n) is equal to 3 and the two-dimensional case where the exponent is equal to 1. Finally, we present the concept of the iterated map and introduce a method for improving the stability properties of the time-stepping method used to solve the ice-sheet equation.
1. Background: The ice-sheet equation and its finite-difference discretizations
The ice-sheet equation is

where H is ice thickness (throughout we deal only with a flat basal topography) and a is the accumulation rate. C is related to the flow law parameter A by

where ρ is the density of ice, g is acceleration due to gravity, A is the ice-flow constant, n is its exponent and the flow relation between strain rate e and deviator stress τ is given by
We deal only with constant A (i.e. with isothermal ice). ∇ is the two-dimensional horizontal gradient operator

and the magnitude of the gradient of |∇H| is computed by

The non-linear diffusion Equation (1) is solved by discretizing the independent variables as

for the horizontal dimensions x and y over the domain −L x ≤ x ≤ L x , −L y ≤ y ≤ L y ;, and
for time t, where N x . and N y are the number of grids in the x and y directions.
1.1. The horizontal space discretization
The discretization of the non-linear diffusion term

calls for some comment. There are many ways of carrying oui a discretization of this operator. Here we define three methods that are in common use and which are schematized in Figure 1. It is convenient to define a coefficient D somewhat analogous to the diffusivity of a thermal medium
so that liquation (1) becomes


Fig. 1. Illustrating the different grids used to compute the coefficient D and the discharge q. The lefthand column slimes which points are used in the computation of the average value of H and |∇H| used in the computation of D, while the righthand column shows the location of D and points used in the evaluation of ∂H/∂x required to compute q.
In method 1, D is evaluated at grid centres which are staggered in both x and y according to

where

and

The x-direction flux q x is then evaluated at x-midway points according to

and similarly for 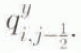 .
.
The y-direction flux q y is evaluated at y-midway points according to

and similarly for 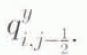 .
.
For method 2, D is evaluated at x-midway and y-midway points which are staggered in the direction of flow only

where

and

The x-direction flux q x is then evaluated at the same x-midway points according to

and similarly for 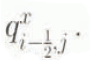 .
.
The y-direction flux q y is evaluated at y-midway points according to

and similarly for 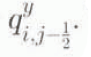 . This scheme derives from Mahaffy (1977).
. This scheme derives from Mahaffy (1977).
In method 3, D is evaluated at the grid points themselves

where

The x-direction flux q x is then evaluated at the staggered x-midway points according to

and similarly for ![]() .
The y-direction flux q
y
is evaluated at y-midway points according to
.
The y-direction flux q
y
is evaluated at y-midway points according to

and similarly for 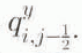 This scheme derives from Oerlemans and Van der Veen (1984) (in one dimension) and Huybrechts (1992) (in two dimensions).
This scheme derives from Oerlemans and Van der Veen (1984) (in one dimension) and Huybrechts (1992) (in two dimensions).
In all three methods, the flux divergence in Equation (4) is computed according to

All these methods are conservative because the thickness calculations at two adjacent grid points (i, j) and (i+ 1, j) both use exactly the same formulation for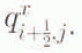 . All the material leaving one grid point arrives at adjacent grid points, except of course at the boundary. However, while methods 1 and 2 have a 9 point computational molecule (for computing the flux gradient), method 3 has a 13 point, computational molecule. This is a very important feature of method 3 and can be interpreted as incorporating an additional, artificial diffusion (or smoothing).
. All the material leaving one grid point arrives at adjacent grid points, except of course at the boundary. However, while methods 1 and 2 have a 9 point computational molecule (for computing the flux gradient), method 3 has a 13 point, computational molecule. This is a very important feature of method 3 and can be interpreted as incorporating an additional, artificial diffusion (or smoothing).
The accuracy of the method 1 and 2 spatial discretizations is not uniform: in the interior of the ice sheet if is second-order, but the singular margins imply that the ice-sheet surface is not analytic and thus that Taylor series do not constitute a valid approximation at these points. Numerical results indicate that the scheme is something like first-order accurate in space.
1.2. The time discretization
We now turn to the discretization of Equation (4) in time, which we denote by

where the superscripts refer the time at which the term is calculated. In particular, the two superscripts on the flux q refer to the time at which the two factors (D k+θ and (∇H) k+ω ) of q are calculated.
We define three lime-stepping schemes. When ω = 1, θ = 0 we have an explicit scheme. When ω = 1, θ = 0 we have the so-called semi-implicit scheme, which is probably the most widely used scheme in glaciology. When ω = 1, θ = 1 we have a fully implicit scheme. In addition to these first-order time discretizations, there is the second-order accurate Crank–Nicholson scheme where ω = 1/2 and θ = 1/2.
The semi-implicit and implicit schemes imply a linear iteration (e.g. a relaxation or a conjugate-gradient method) or a direct matrix-inversion technique (e.g. Gaussian elimination) to solve the linear matrix equation implied by Equation (7). The implicit scheme implies a further, non-linear iteration to cope with the non-linear nature of D. This non-linear iteration may be accomplished by either Picard or Newton–Raphson iteration. These are both well-established techniques which are described in texts on numerical analysis (e.g. Johnson and Riess 1982; Ekman 1987).
We will return to the subject of time stepping in a later section, where the concept of the iterated map will be introduced and used to analyse the stability properties of these time-stepping methods. We now turn to the comparison of the different discretization methods in space and time.
A comparison exercise
In this section we provide comparisons of the accuracy, efficiency and stability of the spatial and temporal discretizations described above. We use two experiments which have analytical solutions available to investigate the effects of spatial discretization on the accuracy of the calculated steady-state ice thickness. We then go on to assess the stability and efficiency of the various time-stepping methods.
Description of the experiments and their analytical solutions
We first describe the two analytical solutions available for steady-state ice thickness.
Experiment I: one dimension with n = 3 In one dimension with constant a, we have from continuity (Vialov, 1958; Nye, 1959)

Over the half-domain y = 0 (divide) to y = L y (margin) with boundary conditions H(0) = H o and H(L y ) = 0, and taking n = 3 we obtain

which can be integrated to

At y = 0

giving

Experiment II: two dimensions with n = 1 In this experiment, we consider the ice-sheet equation for a linear rheology. The flux formula is simply

and the condition for steady state is
with finite flux-boundary conditions on x = ±L x , y = ± L y of H = 0. We may write
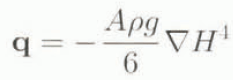
and by defining a new variable u — H 4 we see
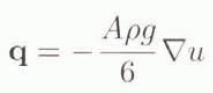
and then obtain
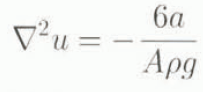
which is simply the Poisson equation on a rectangle, which has an analytical solution (Carslaw and Jaeger, 1988, p. 171). One may then write down the solution for H(x, y), which is

where

1.3. The accuracy of various spatial discretizations
The first set of experiments aims at assessing the behaviour of two spatial discretization methods over various grid resolutions. The discretization methods are the 9 point molecule method 2 and the 13 point molecule method 3 defined above.
A constant time step of 10 years was used for method 2 and a time step of 0.1 year was used in method 3. These time steps assure a stable solution but are not the largest stable time step for each scheme. Time stepping was fully implicit with solution of the non-linear algebraic equations by Newton–Raphson iteration in method 2 and was explicit in method 3, although the various time-stepping methods yield the same results for a given spatial discretization and grid spacing, as we are dealing with steady solutions.
In all experiments, the ice-thickness evolution Equation (1) was integrated from zero ice thickness for 100 kyears, by which time a steady state had been readied. A constant accumulation rate (a) of 0.3 m year−1 was used and the viscosity of ice (A) was set to 10−16 Pa−3 year−1 in experiment I and to 2.1 × 10−7 Pa−1 year−1 in experiment II (resulting in similar ice thicknesses to those of experiment I). In addition, ρ and g were taken as 910 kg m−3 and 9.81 m s−2, respectively. A flat topography was used throughout.
Experiment I: one dimension with n = 3 This experiment was conducted on a rectangular grid on which Δ x = ∆ y . The length of the domain in the y direction was held constant at 1500 km (i.e. 2L y = 1500 km). At the upper and lower edges of the grid, thickness was set to zero. Cyclic boundary conditions were employed on the left and right edges of the domain, so that information passed freely from one boundary to the other. The domain was therefore cylindrical. The ice sheet which evolves should always have symmetry in the y direction about y = 0 km and will have constant thickness along x for any given y. The advantage of this set-up is that, although a two-dimensional problem is solved, the one-dimensional analytical solution above is available for comparison with the results.
Table 1 shows the steady-state divide thicknesses for each run after 100 kyears. In this table and elsewhere, the error ℇ is defined as

where H num is the numerical thickness and H ana the analytical one.
Table 1. Divide thickness found using methods 2 and 3 for various ∆y in experiment I

The analytical solution for the steady-state divide thickness is 3575.058 m. A linear regression on the four runs for method 2 yielded
where ∆ y is the grid spacing in kilometres. This relation has a correlation coefficient of 1.0. The intercept is within 5.5 × 10−5 (0.196 m) of the analytical solution.
The steady-state divide thicknesses obtained in the method 3 experiments are also shown in Table 1. A linear regression on the four runs yielded
with a correlation coefficient of 1.0. The intercept for method 3 is within 7.8 × 10−4 (2.795 m) of the analytical solution.
The very high correlation Coefficients indicate that both spatial discretization methods are first-order accurate and have a linear convergence to the analytical solution as the grid spacing goes to zero. Method 2 is particularly accurate.
figure 2a and b shows the variation of error from the margin to the divide in each of the experiments using, respectively, methods 2 and 3. The relationship between the two schemes’ error remains fairly constant from margin to divide and varies between × 2 and × 3. In all cases, the error grows dramatically towards the margin.

Fig. 2. A comparison of the numerical error from margin to divide using different ∆ y , for spatial discretizations 2(a) and 3(b) in experiment I.
Experiment II: two dimensions with n = 1 This experiment was conducted on a rectangular grid on which Δ x = ∆ y . The length of the domain in the x and y directions was held constant at 1500 km. Ice thickness was set to zero along all four edges of the grid.
Table 2 shows the steady-state divide thicknesses for each run after 100 kyears. The analytical solution for divide thickness is 3551.862 m. A linear regression on the four runs for method 2 yielded

This relation has a correlation coefficient of 1.0. The intercept is within 1.7 × 10−3 (6.021 m) of the analytical solution.
Table 2. Divide thickness found using methods 2 and 3 far various ∆x,y in experiment II

The steady-state divide thickness obtained in the method 3 experiments are also shown in Table 2. A linear regression on the four runs yielded

with a correlation coefficient of −1.0. The intercept for method 3 is within 2.8 × 10−4 (1.010 m) of the analytical solution.
Again, the high correlation coefficients indicate that convergence to the analytical solution is almost linear. However, method 3 is now the more accurate.
figure 3a and b shows the variation of error from the margin (x = 750 km, y = 750 km) to the divide (x = 0 km. y= 750 km) in each of the experiments using, respectively, methods 2 and 3.

Fig. 3. A comparison of the numerical error from margin to divide using different ∆ x,y , for spatial discretizations 2(a) and 3(b) in experiment II.
Both experiments indicate that the accuracy of the spatial discretizations is approximately linear with ∆ x,y . The 9 point molecule discretization (method 2) overestimates steady-state ice thickness mainly because of error in the area of steep surface slopes near the margin. This is particularly true in the n = 1 experiment, where the near-margin surface slopes are much larger than those in the n = 3 experiment. The 13 point molecule discretization (method 3) consistently underpredicts thickness. This is probably because of the apparent artificial diffusion introduced in this discretization (discussed above). In the n = 1 experiment, this diffusion leads to a better overall estimation of steady-state ice thickness.
1.4. The stability and efficiency of various time-stepping discretizations
This experiment is a replication of the EISMINT fixed-margin benchmark, which is two-dimensional and takes n. = 3 (Huybrechts and others, 1996). First, the accuracy of the two spatial discretizations discussed above is again compared, however without the opportunity of comparison with an analytical solution.
Table 3 shows the steady-state divide thicknesses for each run alter 100 kyears. A linear regression on the four runs for method 2 yielded
with a correlation coefficient of 1.0. The linear regression for method 3 yielded
with a correlation coefficient of −1.0. These results are close to those found in the n = 3 one-dimensional experiment above.
Table 3. Divide thickness found using methods 2 and 3 for various ∆x,y in experiment III

The main purpose of this experiment is to compare the efficiency of various time-stepping methods. Three methods are used in combination with spatial discretization method 2. These were the explicit, semi-implicit and implicit methods. In addition, the explicit and semi-implicit methods were used with spatial discretization method 3. No vectorization or parallel techniques were used in the computations.
The semi-implicit and implicit methods require the solution of a sparse, linear system because of the two-dimensional nature of the problem. Here, a conjugate gradient algorithm from Press and others (1992) was used. This will be referred to as the linear iteration. In addition, the implicit method requires the solution of a non-linear system because of the nature of D in Equation (4). A Newton–Raphson partial derivative method was used. This will be called the non-linear iteration. The implicit method therefore has two nested iterations: an outer, non-linear one and an inner, linear one.
The maximum stable time step for each combination of methods is reported in Tables 4–6 for Δ x,y = 75, 50 and 25 km, respectively. Each maximum stable time step was cheeked to the nearest 1 year. The implicit method proved to be very stable and testing was stopped after a 10 kyear time step had been reached. Clearly, this time step is far longer than that required in most practical problems. The runs using the implicit scheme were therefore repeated using 100 year time steps, giving a better impression of the efficiency of this scheme for practical applications.
Table 4. Comparison of spatial discretization and time-stepping methods for ∆x,y = 75 km

Table 5. Comparison of spatial discretization and time-stepping methods for ∆x,y =50 km

Table 6. Comparison if spatial discretization and time-stepping methods for ∆x,y =25 km

The numbers of linear and non-linear iterations, and the normalized (within each table) CPU requirements are also reported in the tables. Although the individual runs lasted for 100 kyears, the ice sheet took approximately 25–27 kyears to reach equilibrium. After this time the number of linear and non-linear iterations required fell dramatically.
The onset of instability depends on the method of time stepping. For explicit and Newton–Raphson implicit stepping, ice thicknesses grow explosively. However, in the semi-implicit method, thicknesses slowly develop oscillations. The criteria for assessing stability was there-fore that the divide thickness should not differ by more than 1 × 10−4 m from the stable thicknesses given in Table 3.
The use of the method 3 spatial discretization allows for a 2–10 times increases the in the maximum stable time step over method 2, which reduces CPU requirement by 3–4 times. The combination of semi-implicit time stepping with this spatial discretization is particularly efficient.
The use of semi-implicit rather than explicit time stepping increases the maximum stable time step by a factor of 5 for spatial discretization 2, and 10 for spatial discretization 3. In terms of CPU requirement, the method is usually twice as efficient.
The comparison of implicit nine stepping with the other methods is difficult. Clearly, when very large time steps are taken, it is much more efficient than either semi-implicit or explicit methods. Much of this advantage is, however, lost when shorter time steps are used, although it remains competitive.
2. The discretized ice-sheet equation as an iterated map
2.1. Scaling
We shall now consider the ice-sheet evolution equations in scaled form. We are still using the equation set (3) and (4). By choosing scales for the thickness [H], the span [L], the accumulation rate [a] and [C] for the quantity C = 2A(ρg) n /( n + 2) which satisfy the relationship

we can consider the ice-sheet equation

in dimensionless form. This scaling is that used in the shallow-ice approximation (e.g. Hutter, 1983) and is described in this volume by Hindmarsh (1996). The time scale is given by
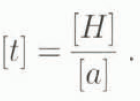
We will restrict consideration to one dimension and, in the following section, zero dimensions.
2.2. Theory: iterated maps of zero-dimensional models
If we make the very crude assumptions that H(x, t) = I(t),J( x), it is easy to show that a scale or zero-dimensional representation of the ice-sheet evolution equation is the ordinary differential equation (ODE)

where I(t) represents the ice-sheet thickness, where we have scaled out the accumulation rate and the rate factor. We note here that the steady solution I = 1 is easily shown to be stable. For the record, this equation does have analytical solutions for particular values of n, including 3, where the solution is given implicitly by

A statement of a range of possible integration schemes is

where k is a counting index and the parameters ϕ,ω ∈ [0, 1] control the iterated map. This map can be written

This will be called “the marching scheme”. Note that schemes with ϕ > 0 involve the solution of a non-linear algebraic equation through the dependence of D on I k+1 . In these schemes, there are two kinds of iterations: the iteration with counting index k, corresponding to a time sequence, and another sequence with counting index ℓ
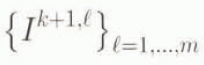
where the I k+1,ℓ represent (we hope), better and better approximations to I k+1, computed from

with

We shall call this the “non-linear iteration”. The computation of sequence is terminated when

where ψ ≪ 1 is the convergence criterion of the nonlinear iteration. We shall be considering four iterated maps, some corresponding to typical ODE integration schemes, while others are not typically used for ODEs, but all have been used for partial differential equations (PDE) and are incorporated for the sake of comparison.
1. Explicit (forward Euler) schemes: ω = 0, ϕ = 0.
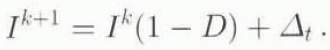
2. Implicit (backward Euler) non-iterated schemes ω = 1, ϕ = 0.

3. Implicit Picard iterated schemes ω = 1, ϕ = 1. A residual, r, is computed, where
and used in the iteration as follows:

4. Implicit Newton–Raphson iterated schemes ω = 1, ϕ = 1. The same residual is used but now a Taylor expansion is used to update the solution:

We shall investigate these maps as a function of the time-step parameter ∆ t . The results are displayed in Figure 4. The first two cases (a) and (b) are the solutions as k → ∞ as a function of the time step. The solution points where computed once transients had decayed. The analytical solution, respected for small time steps, is I = 1. The maps show that for too large time steps the system does not necessarily “blow up” as do related linear equations
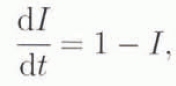
bin go through a period doubling sequence. This occurs at a larger time step for the implicit case than for the explicit ease, but not at a very much greater time step. The explicit case blows up eventually (points not plotted). Cases (c) and (d) represent the iterate as ℓ → ∞. The Picard iteration has worse stability properties than the simple backward Euler scheme on which it is based, while the Newton–Raphson scheme looks very stable.

Fig. 4. Bifurcation maps fur the zero-dimensional ODE model. Vertical axis is I, horizontal axis is ∆ t .(a) is an explicit scheme, (b) is an implicit scheme, (c) is a Picard iteration and (d) is a Newton–Raphson scheme. The points represent successive values of I k as k → ∞ (a and b) and successive values of I k,ℓ as ℓ → ∞ (c and d).
The solution of partial differential equations as iterated maps
By discretizing in time, we are making a fundamental change to the dynamics of the system under consideration, changing it from a dynamical system to an iterated map, i.e. a system of the form
The issue of the stability of numerical schemes is based on establishing some kind of equivalence between the dynamics implied by the iterated map and that of the differential equation which is being investigated.
In solving partial differential equations, we typically arrive at a scheme

where the first superscript represents the time step and the second the iterate; this equation is solved repeatedly for increasing ℓ until the residual

is small in some suitable sense. Certain schemes are not iterated; these can be incorporated in this scheme by considering any residual to be sufficiently small. Certainly, if one maintains a time step short enough to preserve stability and accuracy, the residual will be small. In one dimension, the operators D E, D I are tri-diagonal matrices with rows given by

where 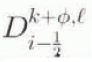 etc. are evaluated according to, for example, Equation (5) and the superscript refers to the time level k + ϕ and iteration ℓ of the vector H
i
. In this case we may identify u
k+ϕ,ℓ
with
etc. are evaluated according to, for example, Equation (5) and the superscript refers to the time level k + ϕ and iteration ℓ of the vector H
i
. In this case we may identify u
k+ϕ,ℓ
with 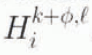 . Similarly,
. Similarly,

Zero margin-elevation boundary conditions simply require that the diagonal entry in the matrix be one.
Then, we can write down the following iterated maps: 1. Explicit schemes
2. Implicit non-iterated schemes

3. Implicit Picard iterated schemes

which can also be written

or

4. Implicit Newton-Raphson iterated schemes

where

There is an important distinction between the first two cases, where the index in the iterated map is the time step, and the latter two cases, where the index in the iterated map is the iteration number. We are going to analyse these iterations as a function of ∆ t in order to find the time steps where the map becomes unstable.
2.3. Stability maps for some finite-difference schemes
We consider some experiments in one dimension, symmetrical about the divide and with a Vialov–Nye fixed margin. The initial elevations are set to be 0.98 (an arbitrary number) times the elevations required for steady state for the discretization under consideration. The schemes are run for various time steps, iterating either as a marching scheme (explicit and semi-implicit schemes) or as non-linear iteration schemes (Picard or Newton–Raphson). For each time step and each scheme, a sequence in k (explicit and semi-implicit) or ℓ was computed for 1024 steps, and the last 256 entries plotted.
Clearly, if the steady-state solution is reached or the iteration converges, all these points will be coincident. If the iteration fails to converge or the stepping is not stable, then for a given time step there will be several points, often reflecting decay on to a periodic or chaotic at tractor. We emphasize that these are manifestations of numerical instability and have no physical meaning. Linearized theory (Hindmarsh, unpublished) predicts exponential decay on to the analytical solution.
The results are plotted in Figure 5. figure 5a shows the results from non-iterated schemes. The explicit scheme gives a maximum time step three times smaller than the maximum time step permissible for the non-iterated scheme, which is indicated by the break in slope. This occurs at time step of around 2 × 10−3; for somewhere like Greenland, where [t] = 10 000 a; this corresponds to a time step of around 20 years. The explicit scheme blows up for too large a time step.

Fig. 5. Bifurcation maps for the iterated maps corresponding to the partial differential equations. Vertical axis is elevation at the divide, horizontal axis is ∆ t . (a) is non-iterated schemes; an explicit scheme (circles) and an implicit non-iterated scheme (dots), (b) is Picard schemes without (circles) and with (dots) unstable manifold iteration, and (c) is Newton–Raphson schemes without (circles) and with (dots) unstable manifold iteration. The points represent successive values of H k as k → ∞ (a) and successive values of H k,ℓ as ℓ → ∞ (b and c). Note how the unstable manifold iteration substantially improves the stability properties of the iterated schemes, in particular the Picard iteration.
If we turn now to the iterated schemes (Fig. 5b and c) the corresponding cases are for when there is “no unstable manifold correction”. This term will be explained in the next section. The Picard iteration is unstable for the whole range of the graph, while the Newton–Raphson iteration shows a stable time step up to around 0.07, corresponding to 700 years in Greenland and 7000 years in East Antarctica.
Note that, for both Picard iteration and Newton–Raphson iteration, the first manifestation of instability is a Hopf bifurcation to an oscillatory steady state with (implied) an unstable steady state.
Application: the correction vector and sub-space under-relaxation
It has been seen that during non-linear iterations, using both the Picard and Newton–Raphson methods, that if the time step is sufficiently large, a Hopf bifurcation occurs and a limit cycle emerges. Associated with this is the fact that if the time step is small enough (presumably relative to the spatial discretization in some unspecified way) then the iterative map “spirals” on to the steady solution. Further increases in the time step result in a typical Feigenbaum-like bifurcation sequence: period doubling, possibly a chaotic region, and, finally (not like a Feigenbaum sequence) blow up.
Detailed investigation not reported here of the iteration sequences shows that only one mode bifurcates as the time step is increased. The other modes remain stable, meaning that after a few (typically two or three iterations) the correction vector simply moves back and forth along the same lint in correction space, with the implication that it is overshooting the unstable solution equivalent to zero error. If one assumes that the movement along this correction line is simply proportional to the error (in effect, linearizing around the solution), then it is possible to compute a correction vector of optimal size, which is moving along the correction line and should, if these assumptions are correct, reach the solution exactly. This procedure amounts to a numerical Taylor expansion of the iteration procedure projected on to the unstable manifold.
Of course there are problems: the decay of the iteration on to the correction line is not instantaneous, so one has to decide when to start this correction procedure; also, one infers the correction line from the correction vectors, so the direction will only be approximately correct. Nevertheless, the results are very promising: not only is convergence of the non-linear iteration accelerated but convergence occurs with this sub-space method when the iteration would otherwise have diverged, because the divergence is along the correction line: the unstable manifold only has dimension one (at least in the region of the solution) while (locally) the remainder of the space is a stable manifold.
We shall work in correction space and not refer to residual space. Let us consider an iterative solution of some non-linear equation which generates a series of approximate solutions x ℓ , x ℓ+1, …, sequence being updated by a sequence of correction vectors c ℓ , c ℓ+1, …, such that x ℓ+1 = x ℓ + c ℓ , and let the error e ℓ , e ℓ+1, … in the solution vector x ℓ , x ℓ+1, …, refer to that which exists before the correction is made. Our heuristic is simply that (c ℓ , c ℓ+1, …) = α(e ℓ , e ℓ+1, …). By the assumption that the decay is on to a straight line in the correction space, we can also simply state that

whence we obtain

and we compute our modified correction vector according to
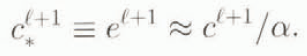
All these norms refer to the two norm. Clearly, this technique will only work if the iteration has converged on to the sub-space. The direction θ between successive correction vectors is easily computed according to the normal projection rule

and the heuristic of the iteration is to decide when this angle is near enough 0 or π for the sub-space iteration to be viable. We have only looked at iterations which were overshooting (thus requiring under-relaxation), and we went as far as sub-space iterating when θ ≥ 5π/6. A typical iteration sequence, as reflected in the value of θ. the sub-space angle, consists of this angle decaying on to a value greater than 5π/6 in two or three iterations, at which point the sub-space iteration is applied. Thereafter, the angle showed a certain amount of variation but seemed to have a value around π/2, which is what one would expect: the correct magnitude of α is being correctly computed but the angle is wrong because of incomplete convergence on to the sub-space, resulting in the solution vector being wrong.
The results of using the unstable manifold correction are shown in figure 5b and c. Picard iteration is stabilized to a time step of around 0.08, while Newton–Raphson iteration is stable to time steps well beyond 0.2. The unstable manifold correction permits significantly enhanced time steps for a small computational investment. When used with Picard iteration, the programming complexity is far less than that for Newton–Raphson iteration.
3. Conclusions
We have investigated the stability and accuracy of a number of different discretizations of the ice-sheet equation from an empirical and a theoretical point of view.
Our analysis of the 9 and 13 point molecule spatial discretizations indicate that both are first order and that they have comparable accuracies. It should be stressed that this finding is true only of the steady-state ice thickness with constant viscosity. We find that fully implicit time-stepping methods can increase the maximum stable time step very dramatically and that they also remain competitive when used with shorter time steps.
The study of a scaled ODE model of the ice-sheet equation can be used as a tool for understanding the mechanisms behind non-linear instability. For increasingly large time steps, this instability has the period-doubling property typical of a Feigenbaum bifurcation sequence, which eventually (not immediately) leads to numerical blow up. These findings prompted the development of a general technique for enhancing the stability of iterated maps using the unstable manifold correction.












