Introduction
Water pressures, p, beneath soft-bedded glaciers often approach flotation levels so effective stresses, h, of 100 kPa and lower are common, even beneath ice that is several kilometers thick. Since the effective stress represents the force per unit area borne by sediment contacts, lower values are associated with lower resistance to sliding, though the rheology of subglacial sediments and the soft-bedded ‘sliding law’ are still debated. Large-scale subglacial water movement normally takes place through conduit systems that occupy a small fraction of the bed area, whereas seepage flows accomplish the local transfer of water between the conduits and the remaining area of the glacier base. If the effective stress near a conduit changes, for example in response to variations in water supply, the changes in effective stress that are communicated to the rest of the glacier base must satisfy the conservation laws that govern the local seepage transport. Here, a framework is developed for predicting the transient effective stress variations that result; two simple cases are examined for illustration.
Borehole measurements of water pressure demonstrate that the effective stress at the glacier bed can vary considerably over short distances, so it is challenging to assess the average value, directly (e.g. Reference Engelhardt and KambEngelhardt and Kamb, 1997; Reference ClarkeClarke, 2005). Observations of glacier movement and geometry can be combined with an understanding of flow rheology and inverse theory to obtain the basal shear resistance, averaged over length scales comparable to the glacier thickness (e.g. Reference Joughin, Tulaczyk, Bindschadler and PriceJoughin and others, 2002). Laboratory shear-strength tests (e.g. Reference Iverson, Hooyer and BakerIverson and others, 1998; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000) suggest that till behaves locally according to Terzaghi’s effective stress principle (Reference TerzaghiTerzaghi, 1943) so that when sliding occurs at effective stress N, τ b = μN, where μ is the coefficient of friction. By contrast, field measurements are interpreted to indicate that increases with strain rate in the deforming sediments beneath (e.g. Reference Boulton and HindmarshBoulton and Hindmarsh, 1987). Hydrological modeling of the variations in p and N holds promise for helping to reconcile these differing viewpoints. The ultimate goal is to develop predictive models for how changes as variations in water supply alter conditions near the basal interface.
The style of subglacial drainage determines the gradients in hydraulic potential, Φ ≡ p + ρ lgz , that are required for large-scale water transport (e.g. Reference Walder and FowlerWalder and Fowler, 1994; Reference ClarkeClarke, 2005). Here ρ l is water density, g the acceleration of gravity and z the elevation above a reference datum. Distributed systems of linked cavities are relatively inefficient in comparison to channelized flow systems, which can transport water over large distances with modest |∇Φ|. In the present work, a larger-scale conduit system of some unspecified description is assumed to be present, but attention is focused on the portions of the glacier bed that are away from the conduits and in direct contact with porous sediments. Perturbations to the pressure in a conduit drive variations in the effective stress at the glacier interface with nearby sediments. The effective stress in the sediments adjacent to the conduit, N C, is prescribed and conservation laws are developed for the manner in which seepage flows communicate imposed variations to the rest of the till–glacier interface.
Model Formulation
Consider a glacier of thickness H that rests on porous till at z = l, which itself sits on impermeable bedrock at z = b, as shown in Figure 1. Darcy’s law gives the transport velocity in the sediments as

Fig. 1. Schematic diagram of the model system. Lateral seepage transport, ū, through the till carries water between the glacier base and the conduit (net melting, i.e. V < 0, is represented here by the wavy arrows in the fringe, where Tl < T < T f and l − h < z < l). Lines of constant Φ are vertical in the water-saturated till above the impermeable bedrock. The effective stress along the assumed sliding surface where z = l − h is N.
where k is the permeability and η is the water viscosity. The sediment thickness, l − b, is assumed small in comparison to lateral scales of seepage flow so u is predominantly in the x-y plane. For the ice–liquid interface to be in thermodynamic equilibrium, a fringe of partially frozen sediments of thickness h must extend beneath the glacier base when N exceeds a level, p f , that is determined by the pore geometry (Reference Dash, Rempel and WettlauferDash and others, 2006; Reference RempelRempel, 2008, Reference Rempel2009). Pore ice reduces the permeability in the fringe so it does not participate significantly in lateral fluid transport. Continuity requires that freezing at the ice–liquid interface at rate V be supplied by flow so the depth-integrated mass-balance condition requires that
where t is time, ϕ is porosity and ρ i is ice density. When net melting takes place at the glacier base, as in the example calculations below, V < 0 and seepage flows transport water toward the conduits. The total normal stress produced by the weight of overlying material is σ. Identifying N = σ n − p as the effective stress level at the furthest extent of pore ice, the average lateral seepage transport through the water-saturated till is approximated from Equation (1) as
Here ρ s is the density of the sediment particles, and the effects of minor terms that arise from the density difference between water and ice are neglected. As indicated on the right-hand side of Equation (3), gradients in N and h both combine with the surface slope to drive seepage transport. The potential effects of bridging stresses are not included in this treatment, but are considered briefly in the discussion section below.
The local rate of freezing or melting (i.e. for V < 0, as is the case in the example calculations below) depends on the heat-balance conditions. In locations where the glacier rests directly upon water-saturated till (i.e. no fringe is present so h = 0), the freezing rate is
where Q b is the basal heat flux into the glacier at z = l, Q g is the geothermal heat flux, Q f is the rate of dissipative heating produced by glacier sliding and L is the latent heat of fusion. In the following, frictional dissipation is assumed to depend on the sliding rate, W s, according to Q f = μNW s. More generally, if a different sediment rheology is found to better describe τ b, the dissipation rate is Q f = τ b W s.
The heat-balance conditions are more complicated in locations where N is sufficiently large (N > p f) that a partially frozen fringe of thickness h > 0 marks the boundary between the glacier and water-saturated till. The ice saturation, S i, in the fringe depends on the local temperature, T , and increases from S i = 0 at its base, z = l −h, where T = T f ; T f is related to the pressure scale for fringe onset by p f = ρ i L(T m −T f)/T m, where T m is the melting temperature at the representative glacial overburden pressure. Changes in temperature, forced for example by changes in Q f that accompany variations in N or W s, produce changes in the fringe ice distribution that are far more important to the energy balance than changes in sensible heat (i.e. the Stefan number is large). Temperature gradients are assumed to be predominantly aligned with the z axis, the ice of the fringe regelates upwards at the freezing rate, V, and heat is conducted with effective thermal conductivity, K e so that the temperature profile through the fringe satisfies (Reference RempelRempel, 2008)
subject to T = T f and −K e ∂T /∂z = Q g + Q f at z = l − h, and −K e ∂T /∂z = Q b − ρ i LV (1 − ϕS i) at z = l. In steady state, Equation (4) remains valid for describing the freezing rate, V. However, the unsteady release of latent heat in the fringe under transient forcing affects how much heat is available for changes in phase right at the glacier base where z = l. Hence, one further boundary condition is required to solve for the temperature profile, the unknown freezing rate, V, and the fringe thickness, h. This is the condition for mechanical equilibrium along the ice–liquid interface, which can be written as (Reference RempelRempel, 2008, Reference Rempel2009)

where Tl is the temperature at z = l. For physical intuition, when N is large enough to require that a fringe be present, the temperature change across it, Tl − T f, is expected to be comparable in size to T m − T f so that h scales with K e(T m −T f)/(Q g + Q f) and can reach up to several meters in thickness.
In this work, for T < T f the constitutive behavior of the till is described using
for the ice saturation and
for the permeability variations with temperature; here k 0 is the permeability of the ice-free till, and α and β are positive empirical constants (Reference Andersland and LadanyiAndersland and Ladanyi, 2004). The form of these functions is suggested by fits to laboratory measurements of ice saturation and permeability in a variety of fine-grained porous media. Unfrozen water is present both in thin films that coat particle surfaces and in larger volumes where the ice surface is highly curved. A more sophisticated treatment would account for differences in the dependence of liquid volume on temperature in these different microscopic reservoirs (e.g. Reference Cahn, Dash and FuCahn and others, 1992; Reference Watanabe and FluryWatanabe and Flury, 2008). For simplicity, and in recognition of the lack of firm experimental constraints on freezing behavior in actual tills, Equations (7) and (8) are favored here, since they introduce the minimum number of empirical parameters. The effective thermal conductivity in the fringe is modeled using
where K s, K i and K l are the thermal conductivities of the solid particles, ice and liquid water, respectively.
Scaled problem
The natural scale for effective stress is p f. Spatial variables are non-dimensionalized by the characteristic sediment thickness, l 0 − b 0; heat fluxes by a typical geothermal flux, Q 0; the sliding rate by W 0 ≡ Q 0 /(μp f); the freezing and water transport rates by V 0 ≡ Q 0 /(ρ i L); time by t 0 ≡ (l 0 − b 0)/V 0; and the reduced temperature is defined as θ ≡ (T m − T)/(T m − T f). The importance of till buoyancy in the fringe is gauged by the dimensionless parameter, ν ≡ (ρ s −ρ i)g(1−ϕ)(l 0 −b 0)/p f. The importance of the glacier surface slope in driving water transport is measured by ≡ ρ i g(l 0 −b 0)/p f. The pressure scale for fringe formation divided by the pressure difference across l 0 − b 0 that ±is required to drive flow at V 0 is Γ ≡ k 0 p f / [η V0 ( l 0 − b 0)]; this is the only dimensionless parameter in this modeling effort that depends on the unfrozen permeability, k 0. The ratio of the temperature depression for pore-ice infiltration to the scale of temperature changes across the sediment layer is κ ≡ K 0 ( T m − T f ) / [ρ iLV0 (l 0 − b0 )], where the thermal conductivity of water-saturated sediment is taken as the characteristic value K 0 so that K e = (K i /K l) S iϕ ≈ 3.9Siϕ .
Equations (2) and (3) combine to be written as

where s ≡ (l − b)/(l 0 − b 0), r ≡ ρ i /ρ l, and widetildes are used to mark the other dimensionless variables. Equation (4) is transformed to give the steady dimensionless freezing rate, which is also valid under transient conditions in regions where the fringe is absent, as
From Equation (5), the reduced temperature within the fringe satisfies
where θ = 1 and κK̃ e ∂θ/∂z = Q̃ g + Ñ W̃ s at z = l̃ − h̃, and κK̃ e ∂θ/∂z̃ = Q̃ b − Ṽ (1 − φS i) at z = l. Using the constitutive behavior from Equations (7) and (8), the force balance condition from Equation (6) is

In this work ϕ has been treated as constant for simplicity.
corresponds to hydrostatic loadings of up to 4 km of ice. For Chena silt, values for T f, k 0, α and β are those of Reference Andersland and LadanyiAndersland and Ladanyi (2004). An attempt was made to account for the fact that some parameters are likely to co-vary and affect the typical ranges summarized in the final column (e.g. small pore size leads to low k 0, T f, and therefore large p f)
Table 1 summarizes nominal parameter values that illustrate the system behavior. The second column contains values for Chena silt, which is expected to have soil parameters that are typical of some fine-grained tills. The third column contains representative values for a more coarse-grained till with a slightly increased ice-infiltration temperature, T f. The unfrozen permeability that is assigned to this model material is estimated based on the pore size that would correspond to the chosen value of T f. That the value of k 0 quoted for the Chena silt is so much lower is likely due, in part, to an increased sensitivity of permeability to temperature changes as T f is approached, which was not captured by the fit to the empirical data summarized by Reference Andersland and LadanyiAndersland and Ladanyi (2004). The final column contains ranges of parameter values that are likely to be of glaciological relevance. The soil parameters that are expected to vary most in different glaciological settings are the ice-infiltration temperature, T f, and the water-saturated permeability, k 0. The former determines the effective stress, N = p f, at which ice first begins to invade the pore space (Reference Dash, Rempel and WettlauferDash and others, 2006; Rempel, 2008, 2009). Even for fine-grained materials such as Chena silt, values of N that exceed a few tens of kPa require that a fringe be present. Sediment thickness and sliding speed both take a large range of values, a subset of which is used to calculate the typical ranges displayed in the final column. Of particular note, the characteristic timescale, t 0, for changes in fringe temperature is always much longer than many of the durations over which changes are inferred from field observations. For cases where h > 0 this separation of timescales is used to aid in calculations of the short-term system response to imposed changes in external forcing.
Table 1. Nominal parameter values. The stated range in Tm corresponds to hydrostatic loadings of up to 4 km of ice. For Chena silt, values for Tf , k0, α and β are those of Andersland and Ladanyi (2004). An attempt was made to account for the fact that some parameters are likely to co-vary and affect the typical ranges summarized in the final column (e.g. small pore size leads to low k0, Tf , and therefore large pf )

Response to changing conduit pressure
A wealth of glaciological observations attests to the common occurrence of rapid changes in basal water supply (e.g. Reference Iken and BindschadlerIken and Bindschadler, 1986; Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002; Reference ClarkeClarke, 2005; Reference Fricker, Scambos, Bindschadler and PadmanFricker and others, 2007; Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008; Reference BellBell, 2008; Reference Price, Payne, Catania and NeumannPrice and others, 2008). For insight into some of the resultant behavior, consider the case of a glacier with uniform thickness and surface slope ψ ≈ ∇(H + l) ⪡ 1 that sits atop a sediment layer of uniform thickness. The y axis is aligned with the downslope direction. It is straightforward to calculate the steady-state effective stress profile at the glacier bed, away from a simple conduit network (Reference RempelRempel, 2009). After achieving a steady state with the effective stress adjacent to a conduit fixed at N C, the pressure is changed rapidly so the new effective stress is N C+ΔN C. The changes to the effective stress profile are assessed next; first for cases in which the entire ice–liquid interface is at N < p f, so no ice infiltrates the pore space, then for cases in which N > p f everywhere at the furthest extent of pore ice so h > 0. These simple cases bracket the more complicated intermediate case where variations in N span a range on either side of p f, so a fringe is present over only part of the glacier base.
No fringe
With no fringe and constant sediment thickness, Equation (10) can be combined with Equation (11) to give
The heat fluxes, Q̃ g and Q̃ b, can be regarded as constant if the timescale, Δt, over which ΔN C is imposed is much longer than the timescale over which thermal diffusion smooths perturbations to the background heat flow. If the pore compressibility is sufficiently small that poroelastic effects are negligible, ∂ϕ/∂t̃ can be neglected and changes in Ñ C are communicated immediately to the surrounding sediments. The effective stress can be written as a perturbation away from the initial profile, N ss, so that N = N ss + ΔN, and Equation (14) implies that
where ![]() is a characteristic decay length.
is a characteristic decay length.
Equation (15) describes the spatial variations to the changes in effective stress that are necessary to maintain previously established hydraulic connections with a conduit system when the near-conduit effective stress is changed by ΔN C.
To illustrate the system behavior, when parallel conduits are separated by scaled distance 2D̃ the change in the horizontally averaged effective stress predicted by Equation (15) is
where n is the coordinate normal to the conduit axis. As shown in Figure 2, Δis a monotonically decreasing function of D̃/d̃. For widely spaced conduits (large D̃) and fast sliding speeds (small d̃) the average effective stress, is relatively insensitive to abrupt changes in N C. This result follows from the general tendency for water flux to increase as conduits are neared because of the integrated effects of ongoing melt supply or removal along the flow path. The gradients in effective stress that drive seepage transport are steepest near conduits and become increasingly shallow further away. For this reason, changes to the effective stress decrease in magnitude as the distance from the flow path to the conduit increases. Even for relatively close conduits and slow sliding speeds, is not perturbed to the same degree as the forced change, ΔN C.

Fig. 2. Predicted change from Equation (16) in the average effective stress normalized by the imposed perturbation, ΔN C, at the conduit margin beneath a glacier with N < p f everywhere, so no fringe is present.
Pervasive fringe
When h̃ > 0 everywhere, for the stated geometry Equations (10) and (13) can be combined to give

The temperature and fringe thickness change on the timescale, t 0, for conduction of latent heat, which is assumed to be much slower than the timescale, Δt, over which ΔN C is imposed. Using h ss to represent the initial steady-state fringe thickness profile and defining I ss using the initial steady-state
θ and h̃ profiles, the short-term change to Ñ satisfies
where poroelastic effects have once more been ignored.
Equation (18) is easily solved numerically, but it is worth commenting on the similarities with Equation (15), particularly for cases where h is either a small or relatively constant fraction of l
0
− b
0 so that the left-hand side of Equation (18) is approximately proportional to As shown for in Figure 2, when h̃ = 0 the predicted change in is a small fraction of the imposed perturbation, ΔN
C, if the conduit spacing is large in comparison to the inverse square-root of the coefficient that multiplies ΔÑ on the right-hand side of Equation (15). For the predictions of Equation (18) to be qualitatively similar, this implies that Δwill be a small fraction of ΔN
C when ![]() where I and h̃ are representative values for the initial steady-state configuration. It is worth noting that unlike the length scale, d̃, that is relevant for cases where a fringe is absent, d̃
f does not depend directly on the unfrozen permeability or sliding rate. When a fringe is present, short-term responses to changes in effective stress require that the freezing rate adjust to satisfy the vertical force balance without immediately changing the fringe-temperature distribution and thickness. Since the steady-state values of h and θl
are influenced by k
0 and W
s, these variables do still exert an indirect control on d̃
f.
where I and h̃ are representative values for the initial steady-state configuration. It is worth noting that unlike the length scale, d̃, that is relevant for cases where a fringe is absent, d̃
f does not depend directly on the unfrozen permeability or sliding rate. When a fringe is present, short-term responses to changes in effective stress require that the freezing rate adjust to satisfy the vertical force balance without immediately changing the fringe-temperature distribution and thickness. Since the steady-state values of h and θl
are influenced by k
0 and W
s, these variables do still exert an indirect control on d̃
f.
An estimate of the decay length, d̃ f, can be obtained using the near-conduit values for fringe thickness, h̃ C and I C. The latter is approximated using a constant fringe temperature gradient
![]()

![]() is found from the solution to Equation (13) for the initial steady-state freezing rate. Figure 3 shows values of d̃
f that result, plotted as a function of Ñ
C with the parameters listed in Table 1 for Chena silt and a sandy till. Subglacial conduit networks with D̃ > d̃
f are expected to require comparatively small short-term changes in in response to imposed changes in N
C. The rapid increase of d̃
f with Ñ
C shown for the sandy till suggests that at high Ñ
C for the same conduit spacing, the sandy till would host a proportionately larger immediate change in than the Chena silt following the same perturbation, ΔN
C. Both I
C and h̃
C depend on the initial steady value of Ñ
C, so that, in contrast to cases where no fringe is present, the decay length, d̃
f, changes with Ñ
C. For example, with Ñ
C
≈ 3, Figure 3 indicates that d̃
f
≈ 1 for both porous media and Figure 2 suggests that when ≈ 2 the value of ΔN
C
≈ 0.5. In fact, since I attains its maximum at I
C when net melting occurs (e.g. due to frictional heating for Q̃
b = Q̃g),d̃
f can be regarded as an approximate upper bound on the decay length; numerical calculations (not shown) demonstrate that the solution to Equation (18) predicts ΔN
C
≈ 0.2 for these values of Ñc and D̃ and the parameters summarized in Table 1 for Chena silt.
is found from the solution to Equation (13) for the initial steady-state freezing rate. Figure 3 shows values of d̃
f that result, plotted as a function of Ñ
C with the parameters listed in Table 1 for Chena silt and a sandy till. Subglacial conduit networks with D̃ > d̃
f are expected to require comparatively small short-term changes in in response to imposed changes in N
C. The rapid increase of d̃
f with Ñ
C shown for the sandy till suggests that at high Ñ
C for the same conduit spacing, the sandy till would host a proportionately larger immediate change in than the Chena silt following the same perturbation, ΔN
C. Both I
C and h̃
C depend on the initial steady value of Ñ
C, so that, in contrast to cases where no fringe is present, the decay length, d̃
f, changes with Ñ
C. For example, with Ñ
C
≈ 3, Figure 3 indicates that d̃
f
≈ 1 for both porous media and Figure 2 suggests that when ≈ 2 the value of ΔN
C
≈ 0.5. In fact, since I attains its maximum at I
C when net melting occurs (e.g. due to frictional heating for Q̃
b = Q̃g),d̃
f can be regarded as an approximate upper bound on the decay length; numerical calculations (not shown) demonstrate that the solution to Equation (18) predicts ΔN
C
≈ 0.2 for these values of Ñc and D̃ and the parameters summarized in Table 1 for Chena silt.

Fig. 3. Approximate decay length, d̃ f, for perturbations in ΔN C with h > 0, calculated using Q̃ b = Q̃ g and the parameters for Chena silt and the sandy till listed in Table 1.
After the initial short-term changes to ΔÑ predicted by Equation (18), further evolution towards a new steady-state profile of effective stress is expected to occur over a timescale of order t 0. Insight into this much more technically challenging problem is provided by the one-dimensional predictions for fringe evolution given by Reference RempelRempel (2008). Examples comparing the qualitative similarities and differences between steady-state effective stress profiles with and without a fringe are given by Reference RempelRempel (2009). While a detailed treatment is beyond the scope of this work, these earlier results suggest that the major conclusion – that effective stress variations decrease in magnitude with distance from a conduit system – is expected to hold as well for the longer-term evolution with finite h.
Discussion and Conclusions
When a glacier sits directly upon water-saturated till and changes in conduit pressure cause abrupt changes, ΔN
C, to the effective stress nearby, the response further away along the glacier–sediment interface decays exponentially over a length scale d ≡ (l
0
−b
0)d̃, that is proportional to the square root of the product of sediment permeability, k
0, with the sediment thickness, l
0 –b
0, divided by the sliding rate, W
s (to be precise: ![]() When the effective stress is higher, so the glacier sits upon ice-infiltrated till (i.e.N > p
f, where p
f is a pressure scale that is determined by the pore geometry), effective stress changes decay over a distance d
f
≡ (l
0
− b
0)d̃
f , that is an increasing function of the initial value of N
C. The rate with which d
f increases with N
C depends on constitutive properties of the till and, in particular, the temperature at which ice first forms within it. Both in cases where a fringe is present and in those where it is not, for conduit spacings, D, that are large in comparison with d or d
f, the predicted change in average effective stress, is a small fraction of ΔN
C. Since significant changes in sliding behavior are inferred from field observations to follow from changes in subglacial water input, this suggests that additional physical mechanisms beyond those considered here must be important in many of these cases.
When the effective stress is higher, so the glacier sits upon ice-infiltrated till (i.e.N > p
f, where p
f is a pressure scale that is determined by the pore geometry), effective stress changes decay over a distance d
f
≡ (l
0
− b
0)d̃
f , that is an increasing function of the initial value of N
C. The rate with which d
f increases with N
C depends on constitutive properties of the till and, in particular, the temperature at which ice first forms within it. Both in cases where a fringe is present and in those where it is not, for conduit spacings, D, that are large in comparison with d or d
f, the predicted change in average effective stress, is a small fraction of ΔN
C. Since significant changes in sliding behavior are inferred from field observations to follow from changes in subglacial water input, this suggests that additional physical mechanisms beyond those considered here must be important in many of these cases.
Large decreases to the average subglacial effective stress can be produced if the water pressure is increased sufficiently to cause flotation. The ‘gap-opening’ model of Reference Engelhardt and KambEngelhardt and Kamb (1997) provides a useful starting point for further consideration of this more complicated problem. The bridging stresses that transfer support for a portion of the glacier weight overlying conduits to the sediments nearby have been ignored in the current work by simply imposing near-conduit values of effective stress, N C; near-conduit boundary layers over which bridging stresses are significant (e.g.Reference NgNg, 2000a,Reference Ngb) have been neglected. Extensions to the gap-opening model will need to take explicit account of these boundary layers to consider the development of the macroscopic water sheet that can separate the glacier from its porous bed following an abrupt increase to the conduit pressure. When the initial value of N C > p f, the presence of a partially frozen fringe further complicates the evolving bed separation (Reference RempelRempel 2008, Reference Rempel2009). A scaling analysis indicates that, while rapid changes to the effective stress along the glacier base are expected following perturbations to N C, when a fringe of partially frozen sediments extends beneath the glacier base its thickness, h, can only change over a characteristic timescale, t 0, that is typically several decades or centuries in length (see Table 1). In many glacier settings, N C is expected to undergo transient changes over much shorter timescales. Indeed, even for steady conduit conditions and nearby effective stress profiles, unless the conduits are aligned with the direction of glacier flow, any given position fixed to the glacier base will experience changes in effective stress as it slides. Since the conduction of latent heat is too slow to enable the fringe thickness, h, and basal temperature profile to equilibrate, h is expected to be controlled by the long-term average effective stress and heat-flow conditions along each basal flowline.
If freeze-on layers develop, they are expected to be thickest where the time-averaged effective stress level is highest. When net melting occurs, N is highest near the conduits, whereas it is highest near drainage divides when net freezing takes place (Reference RempelRempel, 2009). This has implications for patterns of subglacial erosion when h changes along the direction of glacier flow.


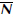 can be produced if conduit spacing is comparatively large and the glacier and sediments remain in contact. To produce larger changes to
can be produced if conduit spacing is comparatively large and the glacier and sediments remain in contact. To produce larger changes to 

