Introduction
Most techniques for assessing the mass balance of ice sheets require measurements of accumulation rate with understood confidence limits. The traditional method of comparing discharge through a gate with catchment input requires the long-term, spatially integrated net accumulation rate. The newer measurement method of comparing the downward velocity of deep (15 m) firn markers with accumulation rate ("coffcc-can method") (Hulbc and Whillans, 1994b; Reference Hamilton, Whillans and MorganHamilton and others, 1998) requires a locally specific long-term mean net accumulation rate. Accumulation rates for both methods are obtained from shallow firn cores or pits. The methods require accurate estimates of confidence in secular and spatial variability.
The motivation for the present work is to place confidence values on snow input to the catchments of Ice Streams B, C and D, Antarctica. Uncertainties arise from measurements of firn density and sample age, spatial and temporal variations, and incomplete sampling of the study area. Data from this region as well as the South Pole are used to estimate the contributions to the error budget. The approach is generic, so the method can be readily applied to other catchment areas.
Data Collection
During field seasons 1983-84 to 1995-96, 80 shallow firn cores were collected in the catchment area of Ice Streams B, C, D and E (Fig. 1). The position of each core is obtained from Transit (early sites) and global positioning system satellite tracking (later sites). Field teams collected cores by hand auger to about 15 m depth and cut them into 0.10-0.30 m lengths. Core densities were measured in the field, as well as in the laboratory.
Accumulation rates are determined from measurements of gross beta activity derived from nuclear bomb test fallout, as described in Reference Pourchet, Pinglot and LoriusPourchet and others (1983) and Whillans and Bindschadler (1988). Core sections are melted and filtered through cation paper to collect 90Sr and 137Cs. Beta emission is measured in a gas-flow proportional counter. The large maximum in beta activity is correlated with the 1964 austral summer accumulation horizon, and the strati-graphically deeper step increase in activity is correlated with the March 1955 horizon. Depths of these marker horizons are used with densityjneasurements to determine the mean accumulation rate, ![]() between the time of each horizon and the collection date.
between the time of each horizon and the collection date.
Some holes were not drilled deep enough to reach the 1955 horizon. However, in cores that reach both date levels, there is little difference between ![]() calculated from the 1964 and 1955 horizons. To obta in the fullest spatial coverage, this study uses
calculated from the 1964 and 1955 horizons. To obta in the fullest spatial coverage, this study uses ![]() calculated from the 1964 horizon, as there is little compromise in the long-term time significance.
calculated from the 1964 horizon, as there is little compromise in the long-term time significance.
Measurement Uncertainty
The accumulation rate from a single core is

where Mi (kg) is the mass of indiv idual core sections, i, above a dated bomb level, and Φ,(m) is the core diameter. The time-span between the age of the dated stratum and core collection is t (a) (Whillans and Bindschadler, 1988).
Measurement errors, ![]() are computed using the first terms in a Taylor series of variations on Equation (1):
are computed using the first terms in a Taylor series of variations on Equation (1):

where t= 24 a (average 1964 bomb horizon age), ![]() is the average core section mass (0.4 kg), Φ is the average diameter (0.076 m), Ν is the average number of core sections (30), UM is the mass uncertainty (0.003 kg, as measured on a temperature-compensated spring scale) and σφ is the uncertainty in the diameters (a conservative value of 0.002 m is assigned to σφ to account for diameter variations in each core section). The uncertainty in the position of gross beta-activity peaks is generally about one sample, which means that the unccrtainty in time interval, at, is 0.7 a for an average 1964 horizon. Combining these values in Equation (2) gives a measurement uncertainty of 0.01 m a−1 ice equivalent (density 920 kg m −3, The result is dominated by the first parenthetical term in Equation (2). The uncertainty resulting from diameter measurements is at least two orders of magnitude larger than the other terms.
is the average core section mass (0.4 kg), Φ is the average diameter (0.076 m), Ν is the average number of core sections (30), UM is the mass uncertainty (0.003 kg, as measured on a temperature-compensated spring scale) and σφ is the uncertainty in the diameters (a conservative value of 0.002 m is assigned to σφ to account for diameter variations in each core section). The uncertainty in the position of gross beta-activity peaks is generally about one sample, which means that the unccrtainty in time interval, at, is 0.7 a for an average 1964 horizon. Combining these values in Equation (2) gives a measurement uncertainty of 0.01 m a−1 ice equivalent (density 920 kg m −3, The result is dominated by the first parenthetical term in Equation (2). The uncertainty resulting from diameter measurements is at least two orders of magnitude larger than the other terms.
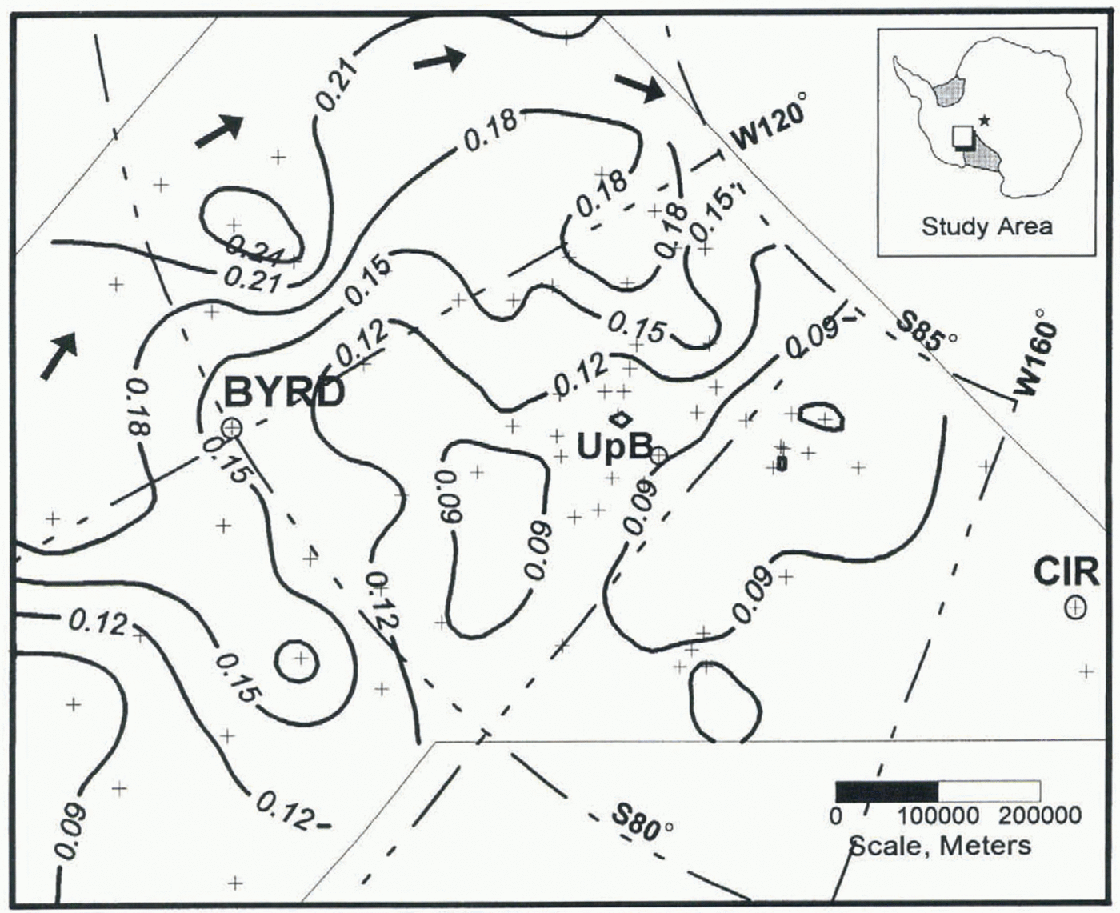
Fig. 1. Accumulation-rate map of the studied part of West Antarctica. Plus signs indicate core locations. Circled plus signs identify labeled core sites. CM denotes Crary Ice Rise. Isolines show accumulation rate (ma−1 ice equivalent). Thin lines show integration limits. Solid arrows represent estimated prevailing storm track. The projection is geocentric.
Core lost in the drilling process has little effect. Core loss is generally 0.1-0.3 m for a 15 m core (1-2%). Missing core sections are assigned the average density of samples above and below the missing section. This effect lends to overestimate accumulation rate slightly as it is usually small-density firn that is lost (Whillans and Bolzan, 1988). Core loss is minor and not considered in the error estimate.
A Model for Variation in Accumulation Rate
Spatial and temporal effects on the reliability of ![]() as a regional long-term mean are considered separately. Despite changes in year-to-year net accumulation rate, the kilo-metcr-scalc spatial pattern remains constant in both West Antarctica (Whillans, 1978) and Dronning Maud Land (Reference Isaksson and KarlénIsaksson and Karlen, 1994). That is, kilometer-scale spatial variations and temporal variations seem to be independent.
as a regional long-term mean are considered separately. Despite changes in year-to-year net accumulation rate, the kilo-metcr-scalc spatial pattern remains constant in both West Antarctica (Whillans, 1978) and Dronning Maud Land (Reference Isaksson and KarlénIsaksson and Karlen, 1994). That is, kilometer-scale spatial variations and temporal variations seem to be independent.
The following subsections describe a conceptual model for the variation in accumulation rate. Following prior works (Reference Giovinetto and MellorGiovinetto, 1964; Reference LliboutryLliboutry, 1974; Whillans and Bindschadler, 1988), measurement errors, combined with spatial and temporal variations, lead to uncertainty in the application of accumulation rate to mass input calculations.
Wind deposition variation
A large amount of snow is transported by wind. This transport results in small-horizontal-scale (10 m) variations in snow deposition due to sastrugi as well as larger-horizontal-scale (~5 km) effects due to the adjustment of katabatic wind speed to undulations in surface topography. Isolated cores, taken without regard to local slope, are affected by both.
Sastrugi include wind-sculpted dunes and troughs. Such features are typically 5-30 m long and about 0.1m high. They are usually developed during a blizzard in freshly deposited snow. A few maps of sastrugi exist (Palais, 1980), but these are insufficient to assess the frequency distribution of sastrugi elevations. Here, sastrugi elevation variation is assumed to be Gaussian.
Measurements of sastrugi roughness are available from two sites in West Antarctica. Along the By rd Station strain network (BSSN) the standard deviation in sastrugi height is 0.02 m ice equivalent (Whillans, 1978). The same result was obtained at the UpB strain grid (Reference Hulbe and WhillansHulbe and Whillans, 1994a) from changes in exposed length of 200 stakes over 1 year. Accumulation rate does not correlate with local slope on the UpB grid, so the variation is taken to be due to sastrugi. The value 0.02 m (ice equivalent) is used in the present error estimate.
Larger-length-scale depositional variations are due to slower katabatic wind speed on less steep slopes. This leads to greater snow deposition on Hatter regions (Whillans, 1975). Surface undulations generally have longitudinal wavelengths of 3 km and slopes of 0.001-0.004 (Gow and others, 1972). Using data from Whillans (1975), the standard deviation of accumulation-rate variation due to surface slope is estimated to be 0.01 m a−1 (ice equivalent).
Interannual variability
Year-to-year variation in precipitation adds further noise to accumulation rate. Whillans (1978) found the interannual variability in accumulation rate to be 0.02 ma−1 ice equivalent (or 16%) from a stake study along the BSSN. Reference Bull and QuamBull (1971) obtained the same results from shallow snow pits near Byrd Station.
Spread of collection dates
Cores were collected over a time-span of 12 years (1983-95). Any changes in accumulation rate during this time could be confused with spatial gradients. No sites were re-occupied after a long time-span, so as to lest for potential secular precipitation changes. No evidence for such a change is found in accumulation rates calculated from the 1955 and 1964 bomb levels. An estimate for this effect is obtained from central East Antarctica, where accumulation-rate changes of up to 20% over 10 years have been measured (Reference Morgan, Goodwin, Etheridge and WookeyMorgan and others, 1991). If such a change occurred between 1983 and 1995, there would be a 0.006 m a−1 change in 20 year accu-mulation-rate averages.
Long-term secular variability
There are longer time-scales of accumulation-rate variation than annual. These are best estimated from long, dated ice cores. One example is the 911 year core from the South Pole (Mosley-Thompson, 1980). The standard deviation of successive 40 year accumulation rates in this core is 0.004 m a−1 (Hulbe and Whillans, 1994b). Reference Hogan and GowHogan and Gow (1997) also present a suitable core from the South Pole. However, at the time of this work there were no suitable cores closer to the study area.
Uncertainty in Accumulation Rate as a Regional and Temporal Mean
The various influences on accumulation rate are taken to combine in a statistical fashion. That is, the true long-term accumulation rate, ![]() , is equal to the measured mean value together with an uncertainty, ϵ:
, is equal to the measured mean value together with an uncertainty, ϵ:
The uncertainty, ϵ, is obtained by combining the various uncertainties (sub-symbols defined in Table 1) discussed above. That is:
Using values from Table 1, and a time of 24 years, the estimate of all uncertainties, ϵ, is 0.016 m a−1 ice equivalem. De-pending on whether regional and temporal, local (coffee-can), or broad-scale (catchment) mean values are sought, all or just some of the terms in Equation (4) are included. The various totals in Table 1 account for this.
Uncertainty in Input Calculation by Catchment Integration
Mass input in the traditional method for mass balance is determined by integrating accumulation rates over the catchment area. The definition of the limits for integration is a separate issue (Reference Price and WhillansPrice and Whillans, 1998) that is not considered here. An arbitrary test area defined by the data coverage is chosen (Fig. 1) for the purpose of estimating uncertainty. This tesi area roughly corresponds to Ice Streams B, C, D and E and their catchments.
Table 1. Values used for uncertainly calculations. The middle column lists the uncertainties in applying the result from a single core to the local region. Rightmost two columns indicate the uncertainly sources thai apply to the localy specific coffee-can and broad-scale catchment input vs discharge mass-balance methods

Not all terms in Equation (4) apply to the accumulation rate used to determine catchment input (table 1). Random variations due to sastrugi, slope effects, and measurement errors tend to cancel with a large number of sites, because these effects are independent from core-to-core. A difference from the error propagation study of Whillans and Bindschadler (1988) is that systematic measurement errors are now considered unimportant. Many different workers measured diameters, making systematic errors due to technique unlikely. Uncertainties related to interannual variability, the spread of core collection dates, and long-term variability may not be eliminated by integration. This is because meteorological events may affect several sites in a similar fashion. For the West Antarctic ice-stream study area, uncertainty is 0.01 ma−1, which translates to a catchment input uncertainty of 0.07 x 1011 m3 a−1 ice equivalent. Compared to a total input of 1.02 x 1011 m3 a−1, this uncertainty is about 7%.
The integration method does not add significant uncertainty. The 1964 accumulation-rate data are fit to a regular grid using a kriging procedure and then integrated numerically with several algorithms contained in Surfer - (Golden Software Inc., 1994). Different interpolation and integration schemes yield virtually identical results.
The effect of site spacing on the results of mass input is estimated by removing data for single sites from poorly sampled areas. Data chosen for removal are those that cause rises or depressions in [he accumulation-rate surface that is not supported by neighboring measurements. Variation in calculated catchment input due to the removal of data from single sites is small (at most, 0.01 x 1011m3a−1 ice equivalent) compared to the uncertainty from temporal variations (0.07 x 1011 m3 a−1). Sparse sampling in catchment areas for individual ice streams may have more important effects.
Conclusions
The model for accumulation-rale variability identifies the major sources of uncertainty for point measurements of accumulation rate and the application of those measurements to mass-balance calculations. For point measurements, the largest uncertainties arise from ![]() (slope effect),
(slope effect), ![]() (time spread) and
(time spread) and ![]() (measurement) (table 1).
(measurement) (table 1). ![]() can be reduced by determining the local slope at the collection point relative to the regional mean. σts can be improved by measuring changes in accumulation rate with an annual resolution or by rc-occupying existing siles.
can be reduced by determining the local slope at the collection point relative to the regional mean. σts can be improved by measuring changes in accumulation rate with an annual resolution or by rc-occupying existing siles.
Improvements to the accuracy of accumulation rate as a long-term spatial mean are dependent on belter diameter measurements. At present, each core-section volume is calculated from only a few diameter measurements. Variations in core diameter are not fully accounted for. Greater accuracy may be obtained for future cores by making more diameter measurements or by measuring core volume by Quid displacement.
For catchment integration, the uncertainty is mainly due to Uít (long-term) and ![]() (table 1). Long-term variation may be reduced by collecting ice cores sufficiently long to average out 20-40 year variations, but this is impractical for the very many cores required for catchment integration. Instead, long-term changes must be included as an uncertainty. The determination of this uncertainty requires the collection of a long core near the study area.
(table 1). Long-term variation may be reduced by collecting ice cores sufficiently long to average out 20-40 year variations, but this is impractical for the very many cores required for catchment integration. Instead, long-term changes must be included as an uncertainty. The determination of this uncertainty requires the collection of a long core near the study area.
Accumulation-rate values presented here are consistent with earlier maps (e.g. Bull, 1971; Giovinetto and Bull, 1987; Whillans and Bindschadler, 1988). The present values are considerably more precise, being based on the objective identification of nuclear bomb levels.
Two spatial trends are apparent in Figure 1. The accumulation rate increases with elevation to the lop and to the left on the map, away from the ice-stream area. Also, the accumulation rate is small in the bottom left corner of the figure (Rockefeller Plateau, Marie Byrd Land).
Trends in accumulation rate are partially due to consistent storm patterns. Storm tracks (Reference Rubin and GiovinettoRubin and Giovinetto, 1962) enter the study area through a saddle in surface elevation around 120° Wand travel south in an are (marked by arrows, Fig. 1), eventually turning west along the north edge of the Transantarctic Mountains, which lie southward and parallel to 85°S. The small accumulation rate in the Rockefeller Plateau (lower left corner, Fig. 1) may be due to the Executive Committee Range to the north, over which fewer snow-bearing storms pass.
Katabatic winds also contribute to the spatial pattern in accumulation rale. Reference Bromwich, Du and ParishBromwich and others (1994) simulated katabatic winds during winter using a three-dimensional model, and reported on ground observations. The area surrounding UpB is found to be an area of accelerating wind speed. Wind speed increases from high elevations (cast) to the ice-strcam region (west), gradually slowing on the ice shelf. Assuming transport is at carrying capacity, areas of accelerating winds should have smaller accumulation rates. in areas of decelerating winds, material drops out of suspension, and the accumulation rate is larger. The accumulation rate is large at high elevations, decreases in the vicinity of the ice streams, and increases again on the ice shelf, in agreement with the katabatic wind-spced pattern and this model of carrying capacity. An alternative interpretation is that areas of small accumulation are due to wind-enhanced sublimation.
Acknowledgements
The cores were collected as part of a joint Ohio State University-NASA field effort. This work was supported by U.S. National Science Foundation grant No. OPP-9316509. This is Byrd Polar Research Center contribution No.C-1080.



