ESTIMATES FOR APPROXIMATE SOLUTIONS TO A FUNCTIONAL DIFFERENTIAL EQUATION MODEL OF CELL DIVISION

Abstract

The functional partial differential equation (FPDE) for cell division,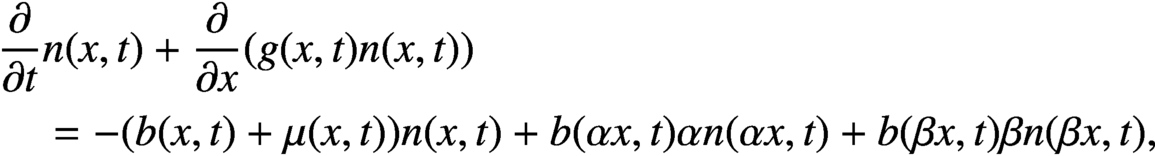

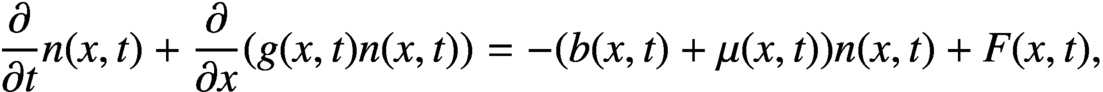
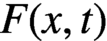$$ \begin{align*} &\frac{\partial}{\partial t}n(x,t) +\frac{\partial}{\partial x}(g(x,t)n(x,t))\\ &\quad = -(b(x,t)+\mu(x,t))n(x,t)+b(\alpha x,t)\alpha n(\alpha x,t)+b(\beta x,t)\beta n(\beta x,t), \end{align*} $$

is not amenable to analytical solution techniques, despite being closely related to the first-order partial differential equation (PDE)

$$ \begin{align*} \frac{\partial}{\partial t}n(x,t) +\frac{\partial}{\partial x}(g(x,t)n(x,t)) = -(b(x,t)+\mu(x,t))n(x,t)+F(x,t), \end{align*} $$

which, with known $F(x,t)$, can be solved by the method of characteristics. The difficulty is due to the advanced functional terms 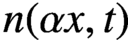$n(\alpha x,t)$ and 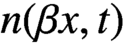$n(\beta x,t)$, where 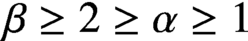$\beta \ge 2 \ge \alpha \ge 1$, which arise because cells of size x are created when cells of size 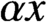$\alpha x$ and 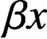$\beta x$ divide.

The nonnegative function, 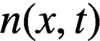$n(x,t)$, denotes the density of cells at time t with respect to cell size x. The functions 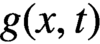$g(x,t)$, 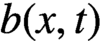$b(x,t)$ and 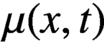$\mu (x,t)$ are, respectively, the growth rate, splitting rate and death rate of cells of size x. The total number of cells, 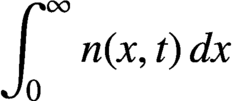$\int _{0}^{\infty }n(x,t)\,dx$, coincides with the 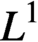$L^1$ norm of n. The goal of this paper is to find estimates in 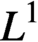$L^1$ (and, with some restrictions, 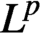$L^p$ for 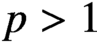$p>1$) for a sequence of approximate solutions to the FPDE that are generated by solving the first-order PDE. Our goal is to provide a framework for the analysis and computation of such FPDEs, and we give examples of such computations at the end of the paper.