No CrossRef data available.
Article contents
An inequality for probability density functions arising from a distinguishability problem
Published online by Cambridge University Press: 17 February 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
An integral inequality is established involving a probability density function on the real line and its first two derivatives. This generalizes an earlier result of Sato and Watari. If f denotes the probability density function concerned, the inequality we prove is that
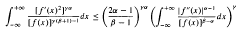
under the conditions β > α 1 and 1/(β+1) < γ ≤ 1.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1998
References
[1] Fernique, X., “Régularité des trajectoires des fonctions aléatoires gaussiennes”, in Lecture Notes in Math. 480 (Springer-Verlag, New York, 1974), pp. 1–96.Google Scholar
[2] Kakutani, S., “On equivalence of infinite product measures”, Ann. of Math. 49 (1948) 214–224.CrossRefGoogle Scholar
[3] Kitada, K. and Sato, H., “On the absolute continuity of infinite product measure and its convolution”, Probab. Theory Related Fields 81 (1989) 609–627.CrossRefGoogle Scholar
[4] Rozanov, Yu. A., “On the density of one Gaussian measure with respect to another”, Theory Probab. Appl. 7 (1962) 82–87.CrossRefGoogle Scholar
[5] Sato, H. and Watari, C., “Some integral inequalities and absolute continuity of a symmetric random translation”, J. Functional Anal. 114 (1993) 257–266.CrossRefGoogle Scholar
[6] Shepp, L. A., “Distinguishing a sequence of random variables from a translate of itself”, Ann. Math. Statist. 36 (1965) 1107–1112.CrossRefGoogle Scholar

