Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T09:11:41.020Z Has data issue: false hasContentIssue false
  • English
  • Français

A functional differential equation arising in modelling of cell growth

Published online by Cambridge University Press:  17 February 2009

A. J. Hall  and
G. C. Wake
A. J. Hall
Affiliation:
Plant Physiology Division, DSIR, Palmerston North, New Zealand, and Department of Mathematics and Statistics, Massey University, Palmerston North, N.Z.
G. C. Wake
Affiliation:
Department of Mathematics and Statistics, Massey University, Palmerston North, N.Z.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A functional differential equation for the steady size distribution of a population is derived from the usual partial differential equation governing the size distribution, in the particular case where birth occurs by one individual of size x dividing into α new individuals of size x/α. 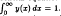This leads, in the case of constant growth and birth rate functions, to the functional differential equation y′(x) = −ay(x) + aαy(αx) together with the integral condition We first look at a number of properties that any solution of this equation and boundary condition must have, and then proceed to find the unique solution by the method of Laplace transforms. Results from number theory on the infinite product found in the solution are presented, and it is shown that y(x) tends to a normal distribution as α → 1+.

Type
Research Article
Information
The ANZIAM Journal , Volume 30 , Issue 4 , April 1989 , pp. 424 - 435
Copyright
Copyright © Australian Mathematical Society 1989

References

[l]Abramowitz, M. and Stegun, I. A., Handbook of mathematical functions (Dover, New York, 1965).Google Scholar
[2]Andrews, G. E., Number theory (W. B. Saunders, Phil., 1971).Google Scholar
[3]Kato, T. and McLeod, J. B., “The functional differential equation y′(x) = ay(λx)+by(x)”, Bull. Amer. Math. Soc. 77 (1971) 891–937.Google Scholar
[4]Sinko, J. W. and Streifer, W., “A model for populations reproducing by fission”, Ecology 52 (1971) 330–335.CrossRefGoogle Scholar