Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T19:19:28.105Z Has data issue: false hasContentIssue false
  • English
  • Français

IMAGE INPAINTING FROM PARTIAL NOISY DATA BY DIRECTIONAL COMPLEX TIGHT FRAMELETS

Part of: Communication, information Nontrigonometric harmonic analysis Numerical methods in Fourier analysis

Published online by Cambridge University Press:  26 May 2017

YI SHEN Open the ORCID record for YI SHEN [Opens in a new window] ,
BIN HAN  and
ELENA BRAVERMAN Open the ORCID record for ELENA BRAVERMAN [Opens in a new window]
YI SHEN*
Affiliation:
Department of Mathematics, Zhejiang Sci-Tech University, Hangzhou 310028, China email yshen@zstu.edu.cn Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, Alberta T6G 2G1, Canada email bhan@ualberta.ca Department of Mathematics and Statistics, University of Calgary, 2500 University Drive N.W., Calgary, Alberta T2N 1N4, Canada email maelena@ucalgary.ca
BIN HAN
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, Alberta T6G 2G1, Canada email bhan@ualberta.ca
ELENA BRAVERMAN
Affiliation:
Department of Mathematics and Statistics, University of Calgary, 2500 University Drive N.W., Calgary, Alberta T2N 1N4, Canada email maelena@ucalgary.ca
*
✉yshen@zstu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Image inpainting methods recover true images from partial noisy observations. Natural images usually have two layers consisting of cartoons and textures. Methods using simultaneous cartoon and texture inpainting are popular in the literature by using two combined tight frames: one (often built from wavelets, curvelets or shearlets) provides sparse representations for cartoons and the other (often built from discrete cosine transforms) offers sparse approximation for textures. Inspired by the recent development on directional tensor product complex tight framelets (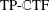$\text{TP}\text{-}\mathbb{C}\text{TF}$s) and their impressive performance for the image denoising problem, we propose an iterative thresholding algorithm using tight frames derived from 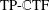$\text{TP}\text{-}\mathbb{C}\text{TF}$s for the image inpainting problem. The tight frame 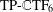$\text{TP}\text{-}\mathbb{C}\text{TF}_{6}$ contains two classes of framelets; one is good for cartoons and the other is good for textures. Therefore, it can handle both the cartoons and the textures well. For the image inpainting problem with additive zero-mean independent and identically distributed Gaussian noise, our proposed algorithm does not require us to tune parameters manually for reasonably good performance. Experimental results show that our proposed algorithm performs comparatively better than several well-known frame systems for the image inpainting problem.

Keywords

noisy dataimage inpaintingdirectional tensor product complex tight frameletssparse representationiterative scheme

MSC classification

Primary: 42C40: Wavelets and other special systems
Secondary: 42C15: General harmonic expansions, frames 65T60: Wavelets 94A08: Image processing (compression, reconstruction, etc.)
Type
Research Article
Information
The ANZIAM Journal , Volume 58 , Issue 3-4 , April 2017 , pp. 247 - 255
Copyright
© 2017 Australian Mathematical Society 

References

Bertalmio, M., Sapiro, G., Caselles, V. and Ballester, C., “Image inpainting”, in: Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques: SIGGRAPH’00 (ACM Press/Addison Wesley Publ. Co., New York, 2000) 417–424; doi:10.1145/344779.344972.Google Scholar
Cai, J.-F., Chan, R. and Shen, Z. W., “A framelet-based image inpainting algorithm”, Appl. Comput. Harmon. Anal. 24 (2008) 131–149; doi:10.1016/j.acha.2007.10.002.Google Scholar
Cai, J.-F., Chan, R. and Shen, Z. W., “Simultaneous cartoon and texture inpainting”, Inverse Probl. Imaging 4 (2010) 379–395; doi:10.3934/ipi.2010.4.379.Google Scholar
Cai, J.-F., Osher, S. and Shen, Z. W., “Split Bregman methods and frame based image restoration”, Multiscale Model. Simul. 8 (2009) 337–369; doi:10.1137/090753504.CrossRefGoogle Scholar
Candès, E. J. and Donoho, D. L., “New tight frames of curvelets and optimal representations of objects with piecewise $C^{2}$ singularities”, Comm. Pure Appl. Math. 57 (2004) 219–266; doi:10.1002/cpa.10116.Google Scholar
Chan, T. F. and Shen, J., Image processing and analysis: variational, PDE, wavelet, and stochastic methods. 1st edn (SIAM, Philadelphia, PA, 2005).Google Scholar
Elad, M., Sparse and redundant representations: from theory to applications in signal and image processing, 1st edn (Springer, New York, 2010).Google Scholar
Elad, M., Starck, J. L., Querre, P. and Donoho, D. L., “Simultaneous cartoon and texture image inpainting using morphological component analysis (MCA)”, Appl. Comput. Harmon. Anal. 19 (2005) 340–358; doi:10.1016/j.acha.2005.03.005.Google Scholar
Han, B., “Nonhomogeneous wavelet systems in high dimensions”, Appl. Comput. Harmon. Anal. 32 (2012) 169–196; doi:10.1016/j.acha.2011.04.002.Google Scholar
Han, B., “Properties of discrete framelet transforms”, Math. Model. Nat. Phenom. 8 (2013) 18–47; doi:10.1051/mmnp/20138102.CrossRefGoogle Scholar
Han, B. and Zhao, Z. P., “Tensor product complex tight framelets with increasing directionality”, SIAM J. Imaging Sci. 7 (2014) 997–1034; doi:10.1137/130928558.Google Scholar
Li, Y. R., Shen, L. X. and Suter, B. W., “Adaptive inpainting algorithm based on DCT induced wavelet regularization”, IEEE Trans. Image Process. 22 (2013) 752–763; doi:10.1109/TIP.2012.2222896.Google Scholar
Lim, W.-Q., “Nonseparable shearlet transform”, IEEE Trans. Image Process. 22 (2013) 2056–2065; doi:10.1109/TIP.2013.2244223.Google Scholar
Sendur, L. and Selesnick, I. W., “Bivariate shrinkage with local variance estimation”, IEEE Signal Process. Lett. 9 (2002) 438–441; doi:10.1109/LSP.2002.806054.Google Scholar
Shen, Y., Han, B. and Braverman, E., “Image inpainting using directional tensor product complex tight framelets”, Preprint, 2014, arXiv:1407.3234.Google Scholar