Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T12:54:33.275Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW LINEAR AND CONSERVATIVE FINITE DIFFERENCE SCHEME FOR THE GROSS–PITAEVSKII EQUATION WITH ANGULAR MOMENTUM ROTATION

Part of: Partial differential equations, initial value and time-dependent initial-boundary value problems

Published online by Cambridge University Press:  08 April 2019

JIN CUI Open the ORCID record for JIN CUI [Opens in a new window] ,
WENJUN CAI ,
CHAOLONG JIANG  and
YUSHUN WANG
JIN CUI
Affiliation:
School of Mathematical Sciences, Jiangsu Key Laboratory for NSLSCS, Nanjing Normal University, Nanjing 210023, China email caiwenjun@njnu.edu.cn, wangyushun@njnu.edu.cn Department of Basic Sciences, Nanjing Vocational College of Information Technology, Nanjing 210023, China email seucj008@163.com
WENJUN CAI
Affiliation:
School of Mathematical Sciences, Jiangsu Key Laboratory for NSLSCS, Nanjing Normal University, Nanjing 210023, China email caiwenjun@njnu.edu.cn, wangyushun@njnu.edu.cn
CHAOLONG JIANG
Affiliation:
School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming 650221, China email Chaolong_jiang@126.com
YUSHUN WANG*
Affiliation:
School of Mathematical Sciences, Jiangsu Key Laboratory for NSLSCS, Nanjing Normal University, Nanjing 210023, China email caiwenjun@njnu.edu.cn, wangyushun@njnu.edu.cn
*
✉wangyushun@njnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A new linear and conservative finite difference scheme which preserves discrete mass and energy is developed for the two-dimensional Gross–Pitaevskii equation with angular momentum rotation. In addition to the energy estimate method and mathematical induction, we use the lifting technique as well as some well-known inequalities to establish the optimal 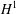$H^{1}$-error estimate for the proposed scheme with no restrictions on the grid ratio. Unlike the existing numerical solutions which are of second-order accuracy at the most, the convergence rate of the numerical solution is proved to be of order 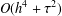$O(h^{4}+\unicode[STIX]{x1D70F}^{2})$ with time step $\unicode[STIX]{x1D70F}$ and mesh size 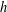$h$. Numerical experiments have been carried out to show the efficiency and accuracy of our new method.

Keywords

Gross–Pitaevskii equationangular momentum rotationfinite difference schemeconservation lawerror estimate

MSC classification

Primary: 65M06: Finite difference methods
Secondary: 65M12: Stability and convergence of numerical methods
Type
Research Article
Information
The ANZIAM Journal , Volume 61 , Issue 2 , April 2019 , pp. 204 - 232
Copyright
© 2019 Australian Mathematical Society 

References

Antoine, X., Bao, W. and Besse, C., “Computational methods for the dynamics of the nonlinear Schrödinger/Gross–Pitaevskii equations”, Comput. Phys. Comm. 184 (2013) 2621–2633; doi:10.1016/j.cpc.2013.07.012.Google Scholar
Antoine, X. and Duboscq, R., “GPELab, a Matlab toolbox to solve Gross–Pitaevskii equations I: Computation of stationary solutions”, Comput. Phys. Comm. 185 (2014) 2969–2991; doi:10.1016/j.cpc.2014.06.026.Google Scholar
Bao, W. and Cai, Y., “Optimal error estimates of finite difference methods for the Gross–Pitaevskii equation with angular momentum rotation”, Math. Comp. 82 (2013) 99–128; doi:10.1090/S0025-5718-2012-02617-2.Google Scholar
Bao, W. and Du, Q., “Computing the ground state solution of Bose–Einstein condensates by a normalized gradient flow”, SIAM J. Sci. Comput. 25 (2004) 1674–1697; doi:10.1137/S1064827503422956.Google Scholar
Browder, F. E., “Existence and uniqueness theorems for solutions of nonlinear boundary value problems”, in: Applications of nonlinear partial differential equations, Volume 17 of Proceedings of Symposia in Applied Mathematics (ed. Finn, R.), (American Mathematical Society, Providence, 1965) 24–49; doi:10.1090/psapm/017/0197933.Google Scholar
Castin, Y. and Dum, R., “Bose–Einstein condensates with vortices in rotating traps”, Eur. Phys. J. D 7 (1999) 399–412; doi:10.1007/s100530050584.Google Scholar
Chang, Q., Jia, E. and Sun, W., “Difference schemes for solving the generalized nonlinear Schrödinger equation”, J. Comput. Phys. 148 (1999) 397–415; doi:10.1006/jcph.1998.6120.Google Scholar
Cloot, A., Herbst, B. M. and Weideman, J. A. C., “A numerical study of the nonlinear Schrödinger equation involving quintic terms”, J. Comput. Phys. 86 (1990) 127–146; doi:10.1016/0021-9991(90)90094-H.Google Scholar
Dalfovo, F. and Giorgini, S., “Theory of Bose–Einstein condensation in trapped gases”, Rev. Mod. Phys. 71 (1999) 463–512; doi:10.1103/RevModPhys.71.463.Google Scholar
Gong, Y. Z., Wang, Q., Wang, Y. S. and Cai, J. X., “A conservative Fourier pseudospectral method for the nonlinear Schrödinger equation”, J. Comput. Phys. 328 (2017) 354–370; doi:10.1016/j.jcp.2016.10.022.Google Scholar
Gray, R., “Toeplitz and circulant matrices”, ISL, Technical Report, Stanford University, Stanford, CA, 2002; https://ee.stanford.edu/∼gray/toeplitz.html.Google Scholar
Guo, B. Y., “The convergence of numerical method for nonlinear Schrödinger equation”, J. Comput. Math. 4 (1986) 121–130; http://www.global-sci.org/v1/jcm/volumes/v4n2/pdf/042-121.pdf.Google Scholar
Hao, C. C., Hsiao, L. and Li, H. L., “Global well posedness for the Gross–Pitaevskii equation with an angular momentum rotational term”, Math. Methods Appl. Sci. 31 (2008) 655–664; doi:10.1002/mma.931.Google Scholar
Henning, P. and Malqvist, A., “The finite element method for the time-dependent Gross–Pitaevskii equation with angular momentum rotation”, SIAM J. Numer. Anal. 55 (2017) 923–952; doi:10.1137/15M1009172.Google Scholar
Lees, M., “Approximate solutions of parabolic equations”, J. Soc. Ind. Appl. Math. 7 (1959) 167–183; doi:10.1137/0107015.Google Scholar
Liao, H. L. and Sun, Z. Z., “Error estimate of fourth-order compact scheme for linear Schrödinger equations”, SIAM J. Numer. Anal. 47 (2010) 4381–4401; doi:10.1137/080714907.Google Scholar
Lieb, E. H. and Seiringer, R., “Derivation of the Gross–Pitaevskii equation for rotating Bose gases”, Commun. Math. Phys. 264 (2006) 505–537; doi:10.1007/s00220-006-1524-9.Google Scholar
Madison, K. W., Chevy, F., Wohlleben, W. and Dalibard, J., “Vortex formation in a stirred Bose–Einstein condensate”, Phys. Rev. Lett. 84 (2000) 806–809; doi:10.1103/PhysRevLett.84.806.Google Scholar
Matthews, M. R., Anderson, B. P., Haljan, P. C., Hall, D. S., Wieman, C. E. and Cornell, E. A., “Vortices in a Bose–Einstein condensate”, Phys. Rev. Lett. 83 (1999) 2498–2501; doi:10.1103/PhysRevLett.83.2498.Google Scholar
Pitaevskii, L. and Stringary, S., Bose–Einstein condensation, Volume 116 of International Series of Monographs on Physics (Clarendon Press, Oxford, 2003).Google Scholar
Shen, J., “A new dual-Petrov–Galerkin method for third and higher odd-order differential equations: application to the KDV equation”, SIAM J. Numer. Anal. 41 (2003) 1595–1619; doi:10.1137/S0036142902410271.Google Scholar
Sun, W. W. and Wang, J. L., “Optimal error analysis of Crank–Nicolson schemes for a coupled nonlinear Schrödinger system in 3D”, J. Comput. Appl. Math. 317 (2017) 685–699; doi:10.1016/j.cam.2016.12.004.Google Scholar
Wang, H., “A time-splitting spectral method for coupled Gross–Pitaevskii equations with applications to rotating Bose–Einstein condensates”, J. Comput. Appl. Math. 205 (2007) 88–104; doi:10.1016/j.cam.2006.04.042.Google Scholar
Wang, T. C., Guo, B. L. and Xu, Q. B., “Fourth-order compact and energy conservative difference schemes for the nonlinear Schrödinger equation in two dimensions”, J. Comput. Phys. 243 (2013) 382–399; doi:10.1016/j.jcp.2013.03.007.Google Scholar
Wang, T. C., Jiang, J. P. and Xue, X., “Unconditional and optimal $H^{1}$ error estimate of a Crank–Nicolson finite difference scheme for the Gross–Pitaevskii equation with an angular momentum rotation term”, J. Math. Anal. Appl. 459 (2018) 945–958; doi:10.1016/j.jmaa.2017.10.073.Google Scholar
Zhang, F., Vłctor, M., Prez, G. and Luis, V., “Numerical simulation of nonlinear Schrödinger systems: a new conservative scheme”, Appl. Math. Comput. 71 (1995) 165–177; doi:10.1016/0096-3003(9400152-T.Google Scholar
Zhou, Y. L., Application of discrete functional analysis to the finite difference methods (International Academic Publishers, Beijing, 1990).Google Scholar