Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cherruault, Y.
Saccomandi, G.
and
Some, B.
1992.
New results for convergence of Adomian's method applied to integral equations.
Mathematical and Computer Modelling,
Vol. 16,
Issue. 2,
p.
85.
Das, Payel
Sahani, Mitali Madhumita
Nelakanti, Gnaneshwar
and
Long, Guangqing
2016.
Legendre Spectral Projection Methods for Fredholm–Hammerstein Integral Equations.
Journal of Scientific Computing,
Vol. 68,
Issue. 1,
p.
213.
Mandal, Moumita
and
Nelakanti, Gnaneshwar
2017.
Superconvergence of Legendre spectral projection methods for Fredholm–Hammerstein integral equations.
Journal of Computational and Applied Mathematics,
Vol. 319,
Issue. ,
p.
423.
Panigrahi, Bijaya Laxmi
2018.
Mathematics and Computing.
Vol. 253,
Issue. ,
p.
315.
Panigrahi, Bijaya Laxmi
2018.
Legendre Spectral Projection Methods for Hammerstein Integral Equations with Weakly Singular Kernel.
International Journal of Applied and Computational Mathematics,
Vol. 4,
Issue. 6,
Panigrahi, Bijaya Laxmi
2019.
Error analysis of Jacobi spectral collocation methods for Fredholm-Hammerstein integral equations with weakly singular kernel.
International Journal of Computer Mathematics,
Vol. 96,
Issue. 6,
p.
1230.
Allouch, C.
Sbibih, D.
and
Tahrichi, M.
2019.
Legendre superconvergent Galerkin-collocation type methods for Hammerstein equations.
Journal of Computational and Applied Mathematics,
Vol. 353,
Issue. ,
p.
253.
Chakraborty, Samiran
and
Nelakanti, Gnaneshwar
2021.
Approximation methods for system of nonlinear Fredholm–Hammerstein integral equations.
Computational and Applied Mathematics,
Vol. 40,
Issue. 1,
Mandal, Moumita
and
Nelakanti, Gnaneshwar
2021.
Superconvergence results for the nonlinear Fredholm–Hemmerstein integral equations of second kind.
The Journal of Analysis,
Vol. 29,
Issue. 1,
p.
67.
Allouch, C.
Arrai, M.
Bouda, H.
and
Tahrichi, M.
2023.
Legendre superconvergent degenerate kernel and Nyström methods for nonlinear integral equations.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 75,
Issue. 5,
p.
579.
Allouch, C.
Sbibih, D.
and
Tahrichi, M.
2023.
Spectral approximation methods for nonlinear integral equations with non-smooth kernels.
Calcolo,
Vol. 60,
Issue. 2,
Bouda, Hamza
Allouch, Chafik
and
Boujraf, Ahmed
2024.
New Trends in Shape Modelling and Approximation Methods.
Vol. 37,
Issue. ,
p.
141.
Fermo, Luisa
Laguardia, Anna Lucia
Laurita, Concetta
and
Russo, Maria Grazia
2025.
A global approximation method for second-kind nonlinear integral equations.
Applied Mathematics and Computation,
Vol. 487,
Issue. ,
p.
129094.
Chakraborty, Samiran
Kumar Agrawal, Shivam
and
Nelakanti, Gnaneshwar
2025.
Superconvergent spectral projection and multi-projection methods for nonlinear Fredholm integral equations.
International Journal of Computer Mathematics,
Vol. 102,
Issue. 2,
p.
389.

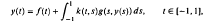
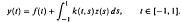
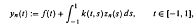
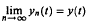 , uniformly in
, uniformly in 