Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chu, Eric King-wah
Huang, Tsung-Ming
Lin, Wen-Wei
and
Wu, Chin-Tien
2010.
PALINDROMIC EIGENVALUE PROBLEMS: A BRIEF SURVEY.
Taiwanese Journal of Mathematics,
Vol. 14,
Issue. 3A,
Chen, Xiao Shan
Li, Wen
and
Ng, Michael K.
2012.
Perturbation Analysis for Antitriangular Schur Decomposition.
SIAM Journal on Matrix Analysis and Applications,
Vol. 33,
Issue. 2,
p.
325.
Wu, Jia Yan
Chen, Xiao Shan
and
Sun, Hai–Wei
2026.
Componentwise and normwise perturbation analysis for the anti-triangular Schur decomposition.
Journal of Computational and Applied Mathematics,
Vol. 476,
Issue. ,
p.
117092.

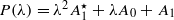 with
with 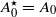 (where
(where 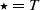 or
or 