Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T05:02:54.398Z Has data issue: false hasContentIssue false
  • English
  • Français

SIMPLE JOINT INVERSION LOCALIZED FORMULAE FOR RELAXATION SPECTRUM RECOVERY

Part of: Integral equations, integral transforms Foundations, constitutive equations, rheology Volterra integral equations Theoretical approximation of solutions

Published online by Cambridge University Press:  05 July 2016

R. S. ANDERSSEN ,
A. R. DAVIES ,
F. R. de HOOG  and
R. J. LOY Open the ORCID record for R. J. LOY [Opens in a new window]
R. S. ANDERSSEN*
Affiliation:
CSIRO Data61, GPO Box 664, Canberra, ACT 2601, Australia email Bob.Anderssen@csiro.au, Frank.deHoog@csiro.au
A. R. DAVIES
Affiliation:
Mathematics, University of Cardiff, Cardiff, UK email DaviesR@cardiff.ac.uk
F. R. de HOOG
Affiliation:
CSIRO Data61, GPO Box 664, Canberra, ACT 2601, Australia email Bob.Anderssen@csiro.au, Frank.deHoog@csiro.au
R. J. LOY
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, ACT 2601, Australia email Rick.Loy@anu.edu.au
*
✉Bob.Anderssen@csiro.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In oscillatory shear experiments, the values of the storage and loss moduli, 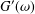$G^{\prime }(\unicode[STIX]{x1D714})$ and 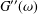$G^{\prime \prime }(\unicode[STIX]{x1D714})$, respectively, are only measured and recorded for a number of values of the frequency $\unicode[STIX]{x1D714}$ in some well-defined finite range 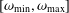$[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$. In many practical situations, when the range 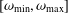$[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$ is sufficiently large, information about the associated polymer dynamics can be assessed by simply comparing the interrelationship between the frequency dependence of 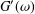$G^{\prime }(\unicode[STIX]{x1D714})$ and 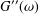$G^{\prime \prime }(\unicode[STIX]{x1D714})$. For other situations, the required rheological insight can only be obtained once explicit knowledge about the structure of the relaxation time spectrum 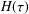$H(\unicode[STIX]{x1D70F})$ has been determined through the inversion of the measured storage and loss moduli 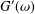$G^{\prime }(\unicode[STIX]{x1D714})$ and 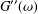$G^{\prime \prime }(\unicode[STIX]{x1D714})$. For the recovery of an approximation to 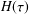$H(\unicode[STIX]{x1D70F})$, in order to cope with the limited range 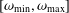$[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$ of the measurements, some form of localization algorithm is required. A popular strategy for achieving this is to assume that 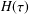$H(\unicode[STIX]{x1D70F})$ has a separated discrete point mass (Dirac delta function) structure. However, this expedient overlooks the potential information contained in the structure of a possibly continuous 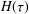$H(\unicode[STIX]{x1D70F})$. In this paper, simple localization algorithms and, in particular, a joint inversion least squares procedure, are proposed for the rapid recovery of accurate approximations to continuous 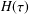$H(\unicode[STIX]{x1D70F})$ from limited measurements of 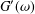$G^{\prime }(\unicode[STIX]{x1D714})$ and 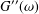$G^{\prime \prime }(\unicode[STIX]{x1D714})$.

Keywords

relaxation spectrum approximationoscillatory shear datajoint inversionnumerical differentiationrheology

MSC classification

Primary: 45L05: Theoretical approximation of solutions
Secondary: 45D05: Volterra integral equations 65R20: Integral equations 76A05: Non-Newtonian fluids
Type
Research Article
Information
The ANZIAM Journal , Volume 58 , Issue 1 , July 2016 , pp. 1 - 9
Copyright
© 2016 Australian Mathematical Society 

References

Anderssen, R. S., Davies, A. R., de Hoog, F. R. and Loy, R. J., “Derivative based algorithms for continuous relaxation spectrum recovery”, J. Non-Newtonian Fluid Mech. 222 (2015) 132–140; doi:10.1016/j.jnnfm.2014.10.004.Google Scholar
Anderssen, R. S. and de Hoog, F. R., “Finite-difference methods for the numerical differentiation of non-exact data”, Computing 33 (1984) 259–267; doi:10.1007/BF02242272.Google Scholar
Anderssen, B., de Hoog, F. and Hegland, M., “A stable finite difference ansatz for higher order differentiation of non-exact data”, Bull. Aust. Math. Soc. 58 (1998) 223–232; doi:10.1017/S0004972700032196.Google Scholar
Anderssen, R. S. and Hegland, M., “For numerical differentiation, dimensionality can be a blessing!”, Math. Comput. 68 (1999); doi:10.1090/S0025-5718-99-01033-9.Google Scholar
Anderssen, R. S. and Hegland, M., “Derivative spectroscopy - An enhanced role for numerical differentiation”, J. Integral Equations Appl. 22 (2010) 355–367; doi:10.1216/JIE-2010-22-3-355.CrossRefGoogle Scholar
Davies, A. R. and Anderssen, R. S., “Sampling localization in determining the relaxation spectrum”, J. Non-Newtonian Fluid Mech. 73 (1997); doi:10.1016/S0377-0257(97)00056-6.CrossRefGoogle Scholar
Davies, A. R. and Goulding, N. J., “Wavelet regularization and the continuous relaxation spectrum”, JNNFM 189 (2012) 19–30; doi:10.1016/j.jnnfm.2012.09.002.Google Scholar
Ferry, J. D., Viscoelastic properties of polymers (Wiley, New York, 1980).Google Scholar
Fuoss, R. M. and Kirkwood, J. G., “Electrical properties of solids. VIII. Dipole moments in polyvinyl chloride-diphenyl systems”, J. Amer. Chem. Soc. 63 (1941) 385–394; doi:10.1021/ja01847a013.CrossRefGoogle Scholar
Groot, R. D. and Agterof, W. G. M., “Dynamic viscoelastic modulus of associative polymer networks – off-lattice simulations, theory and comparison to experiments”, Macromolecules 28 (1995) 6284–6295; doi:10.1021/ma00122a041.Google Scholar
Honerkamp, J. and Weese, J., “Determination of the relaxation spectrum by a regularization method”, Macromolecules 22 (1989) 4372–4377; doi:10.1021/ma00201a036.CrossRefGoogle Scholar
Honerkamp, J. and Weese, J., “A nonlinear regularization method for the calculation of relaxation spectra”, Rheologica Acta 32 (1993) 65–73; doi:10.1007/BF00396678.Google Scholar
Jupp, D. L. B. and Vozoff, K., “Stable iterative methods for the inversion of geophysical data”, Geophys. J. R. Astro. Soc. 42 (1975) 957–976; doi:10.1111/j.1365-246X.1975.tb06461.x.Google Scholar
Malkin, A. Ya., “The use of a continuous relaxation spectrum for describing the viscoelastic properties of polymers”, Polymer Sci. A 48 (2006) 39–45; doi:10.1134/S0965545X06010068.Google Scholar
Schwarzl, F. and Staverman, A. J., “Higher approximation methods for the relaxation spectrum from static and dynamic measurements of visco-elastic materials”, Appl. Sci. Res. A 4 (1953) 127–141; http://link.springer.com/article/10.10072FBF03184944.CrossRefGoogle Scholar
Tanner, R. I. and Walters, K., Rheology: an historical perspective (Elsevier, Amsterdam, 1998).Google Scholar
Tschoegl, N. W., The phenomenological theory of linear viscoelastic behavior: an introduction (Springer, Berlin, 1989).Google Scholar
Walters, K., Rheometry (Chapman and Hall, London, 1975).Google Scholar