Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T22:27:39.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Some multivariable Gaussian hypergeometric extensions of the Preece theorem

Published online by Cambridge University Press:  17 February 2009

M. I. Qureshi ,
M. Sadiq Khan ,
M. A. Pathan  and
N. U. Khan
M. I. Qureshi
Affiliation:
Department of Applied Sciences and Humanities, Faculty of Engineering and Technology, Jamia Millia Islamia, New Delhi-110025, India.
M. Sadiq Khan
Affiliation:
Department of Mathematics, Shibli National College, Paharpur, Azamgarh, U.P., India; e-mail: mohdsadiq786@rediffmail.com.
M. A. Pathan
Affiliation:
Department of Mathematics, Aligarh Muslim University, Aligarh-202002, India; e-mail: mapathan@gmail.com, nabi-khan@rediffmail.com.
N. U. Khan
Affiliation:
Department of Mathematics, Aligarh Muslim University, Aligarh-202002, India; e-mail: mapathan@gmail.com, nabi-khan@rediffmail.com.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some generalisations of the Preece theorem involving the product of two Kummer's functions 1F1 are obtained using Dixon's theorem and some well-known identities. Its special cases yield various new transformations and reduction formulae involving Pathan's quadruple hypergeometric function 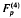and Srivastava's quadruple hypergeometric function F(4) and triple hypergeometric function F(3). Some known results of Preece, Pathan and Bailey are also obtained as special cases.

Keywords

Dixon's theoremPreece's theoremmultiple Gaussian hypergeometric functions.
Type
Research Article
Information
The ANZIAM Journal , Volume 48 , Issue 1 , July 2006 , pp. 143 - 150
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Bailey, W. N., “On the sum of a terminating 3F2(1)”, Quart J. Math. (Oxford) Series (2) 4 (1953) 237–240.CrossRefGoogle Scholar
[2]Exton, H., Multiple hypergeometric functions and applications (Halsted Press (Ellis Horwood, Chichester, UK), John Wiley and Sons, New York, Chichester, Brisbane and Toronto, 1976).Google Scholar
[3]Exton, H., “Hypergeometric functions of three variables”, J. Indian Acad. Math. 4 (1982) 113–119.Google Scholar
[4]Lauricella, G., “Sulle funzioni ipergeometriche a piu variabili”, Rend. Circ. Mat. Palermo 7 (1893) 111–158.CrossRefGoogle Scholar
[5]Pathan, M. A., “On some transformations of triple hypergeometric series F(3)-III”, Indian J. Pure Appl. Math. 9 (1978) 1113–1117.Google Scholar
[6]Pathan, M. A., “On a transformation of a general hypergeometric series of four variables”, Nederl. Akad. Wetensch. Proc. Ser. A, 82 = Indag. Math. 41 (1979) 171–175.CrossRefGoogle Scholar
[7]Preece, C. T., “The product of two generalized hypergeometric functions”, Proc. London Math.Soc. (2) 22 (1924) 370–380.CrossRefGoogle Scholar
[8]Rainville, E. D., Special functions (Macmillan, New York, 1960; Reprinted by Chelsea, Bronx, New York, 1971).Google Scholar
[9]Srivastava, H. M., “A formal extension of certain generating functions-II”, Glasnik Mat. Ser. III 26 (1971) 35–44.Google Scholar
[10]Srivastava, H. M., “Generalized Neumann expansions involving hypergeometric functions”, Proc. Cambridge Philos. Soc. 63 (1976) 445–429.Google Scholar
[11]Srivastava, H. M. and Daoust, M. C., “Certain generalized Neumann expansions associated with Kampé de Fériet function”, Nederl. Akad. Wetensch. Proc. Ser. A, 72 = Indag. Math. 31 (1969) 449–157.Google Scholar
[12]Srivastava, H. M. and Karlsson, P. W., Multiple Gaussian Hypergeometric Series (Halsted Press (Ellis Horwood, Chichester, UK), John Wiley and Sons, New York, Chichester, Brisbane and Toronto, 1985).Google Scholar
[13]Srivastava, H. M. and Manocha, H. L., A Treatise on Generating Functions (Halsted Press (Ellis Horwood, Chichester, UK), John Wiley and Sons, New York, Chichester, Brisbane and Toronto, 1984).Google Scholar