I. INTRODUCTION
The past decade has witnessed a surge in immersive audio systems, ranging from professional systems in cinemas to consumer grade systems for domestic, automotive, VR/AR, and mobile platforms. New developments in 5G, edge computing, smart sensing, and AI create new frontiers for heightened level of immersive experience. As the slogan of 2019 AES International Conference on Immersive and Interactive Audio puts it: Creating the next dimension of sound experience.
In this review, the author introduces the acquisition, transmission, and rendering algorithms of immersive audio technologies, touching upon both software and hardware. The content is organized as the followings. First an introduction to immersive audio is provided. Secondly, the immersive audio capture and creation is described. This is followed by immersive audio storage and transmission. Then the rendering and playback of immersive audio is explored. Finally, the review is concluded by a brief touch of industry trend and applications.
A) Immersive audio overview
It becomes generally agreed that an immersive audio system consists of three categories: channel-based audio (CBA), object-based audio (OBA), and scene-based audio (SBA).
Conventional 5.1/7.1 surround sound formats are typical examples of CBA systems. The latest immersive audio systems are mostly object-based, where Dolby Atmos and MPEG-H are dominant commercial brands on the market. MPEG-H also includes a sophisticated HOA component, allowing SBA audio.
The film and television industry (The Society of Motion Picture and Television Engineers) SMPTE 2098 series aims at standardizing immersive audio, allowing different providers can exchange their bitstreams. The bulk of its specification is based on Dolby Atmos [1], but at the same time it also allows other systems to be compatible within this protocol.
The new immersive audio is no longer limited to the horizontal plane. With the addition of ceiling speakers, height information is fully supported. For example, in a home theater scenario, the conventional 5.1 becomes 5.1.2, which means two speakers on top, or 7.1.4, which means four speakers on top. When proper audio elements are presented, the addition of height information generates a strong sense of immersion not conveniently experienced in the legacy channel systems.
This change is difficult to achieve if it stays in the traditional 5.1 format. Although the traditional way to simulate the height information is to spread the layers, it does not fundamentally change the underlying architecture in terms of content creation and rendering. On the other hand, treating height information with the horizontal plane in a unified way in modern object-based systems actually represents a significant change to the immersive audio production in the film and television industry. The full 3D space production system promises higher accuracy of localization rendering, a more immersive experience.
It's been known that adding interactivity would greatly enhance the immersive experience. The rise of AR and VR in the past few years makes interactivity an indispensable feature. For example, the head tracking and rotation of VR head display equipment not only need to rotate the video, but also need to rotate the sound field. While interactivity in traditional 5.1 audio (pre-mixed) is difficult to achieve, new rendering techniques and immersive audio architecture make it technically possible.
With the new immersive audio architecture, the end users are empowered with more flexibility. For example, when watching TV programs, a user can flexibly choose different languages according to different occasions, and choose different directions in the sound field to experience. These are achieved by transferring an object or metadata for manipulating a sound field, which is not possible with traditional 5.1 or stereo transmission.
Finally, the latest development of immersive audio has fundamentally changed the paradigm of content creation workflow. Most notably by describing audio object with metadata, the mixing engineers are no longer limited by a fixed 5.1 loudspeaker arrangement when describing a sound scene. This separation of content creation from the actual playback venues makes the system agnostic to vast heterogeneous rendering devices. Whether it's 5.1 speakers, stereo headphones, or other devices, mixing is done by software algorithms in the rendering engine. The concept of “mix once, play everywhere” is flagged as one of the strongest selling point of the new immersive audio systems.
B) Channel-based audio
In CBA, various sound sources are mixed, typically in a digital audio workstation (DAW), to create a final channel-based mix for a pre-defined target loudspeaker layout (Fig. 1).
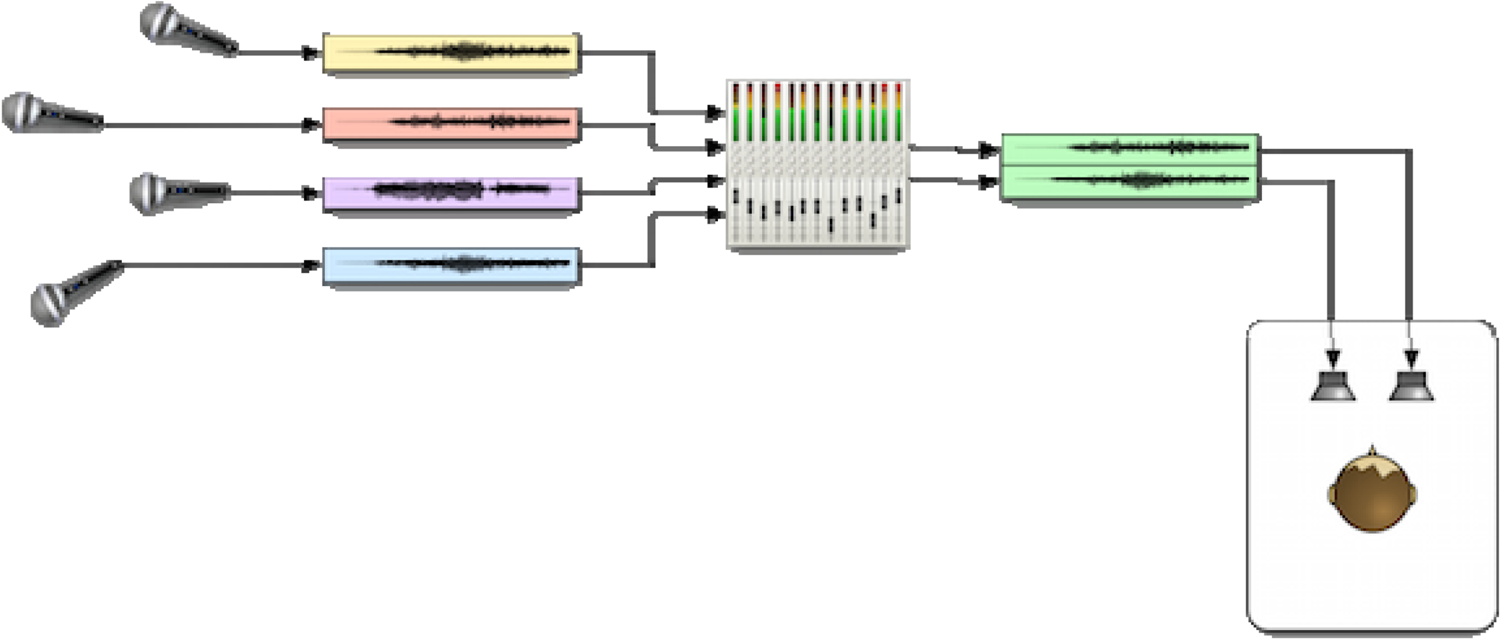
Fig. 1. Channel-based audio system, courtesy (https://lab.irt.de/demos/object-based-audio/).
Playing back CBA is fairly straightforward, as signals are pre-mixed for each loudspeaker. As shown below, a 5.1 surround sound system assumes a fixed channel/loudspeaker position, which is composed of Front L (L), Front Right (R), Center (C), Left Surround (LS), Right Surround (RS), and the low frequency channel (LFE). 7.1 is to add two additional rear surround channels on the basis of 5.1. As defined in SMPTE ST 428-12, the channel order is L, R, C, LFE, Ls, Rs for 5.1 and L, R, C, LFE, Lss, Rss, Lrs, Rrs for 7.1.
More advanced renderers, as already described in the MPEG-H 3D audio, would contain downmix and upmix modules when the input content format does not match the playback loudspeaker setup (Fig. 2).
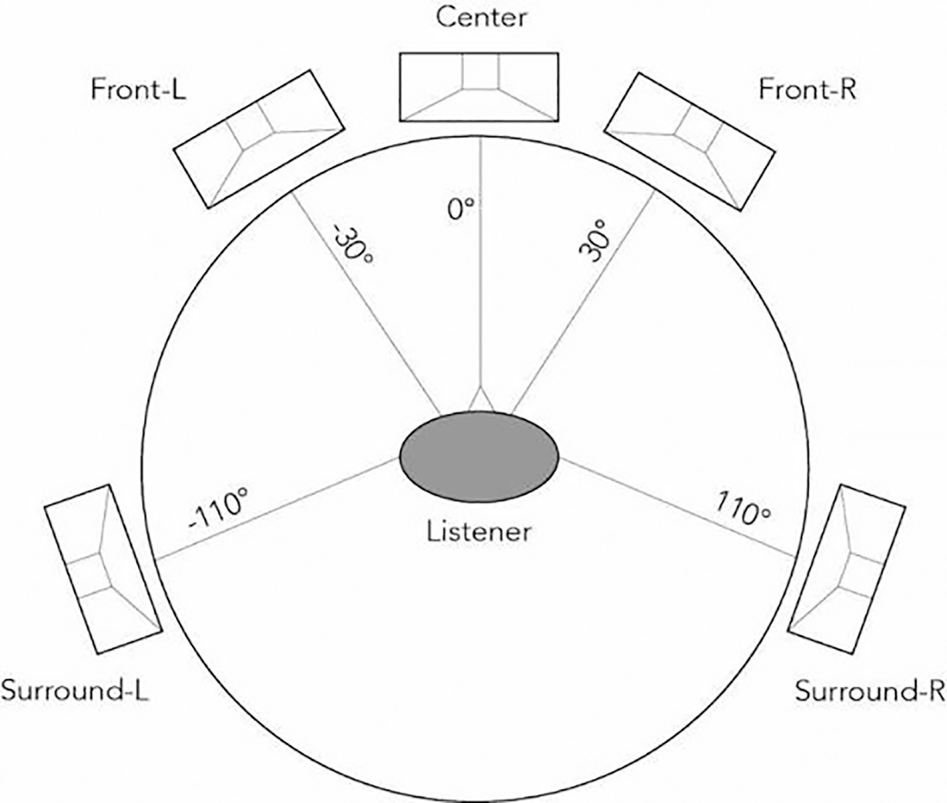
Fig. 2. 5.1 loudspeaker placement.
C) Object audio
It can be seen from above that such a pre-mixed channel system lacks of much-needed flexibility when it comes to user personalization and interactivity. An object-audio approach is able to overcome these limitations through describing the representation of media content by a set of individual assets, together with metadata describing their relationships and associations (https://lab.irt.de/demos/object-based-audio/) (Fig. 3).
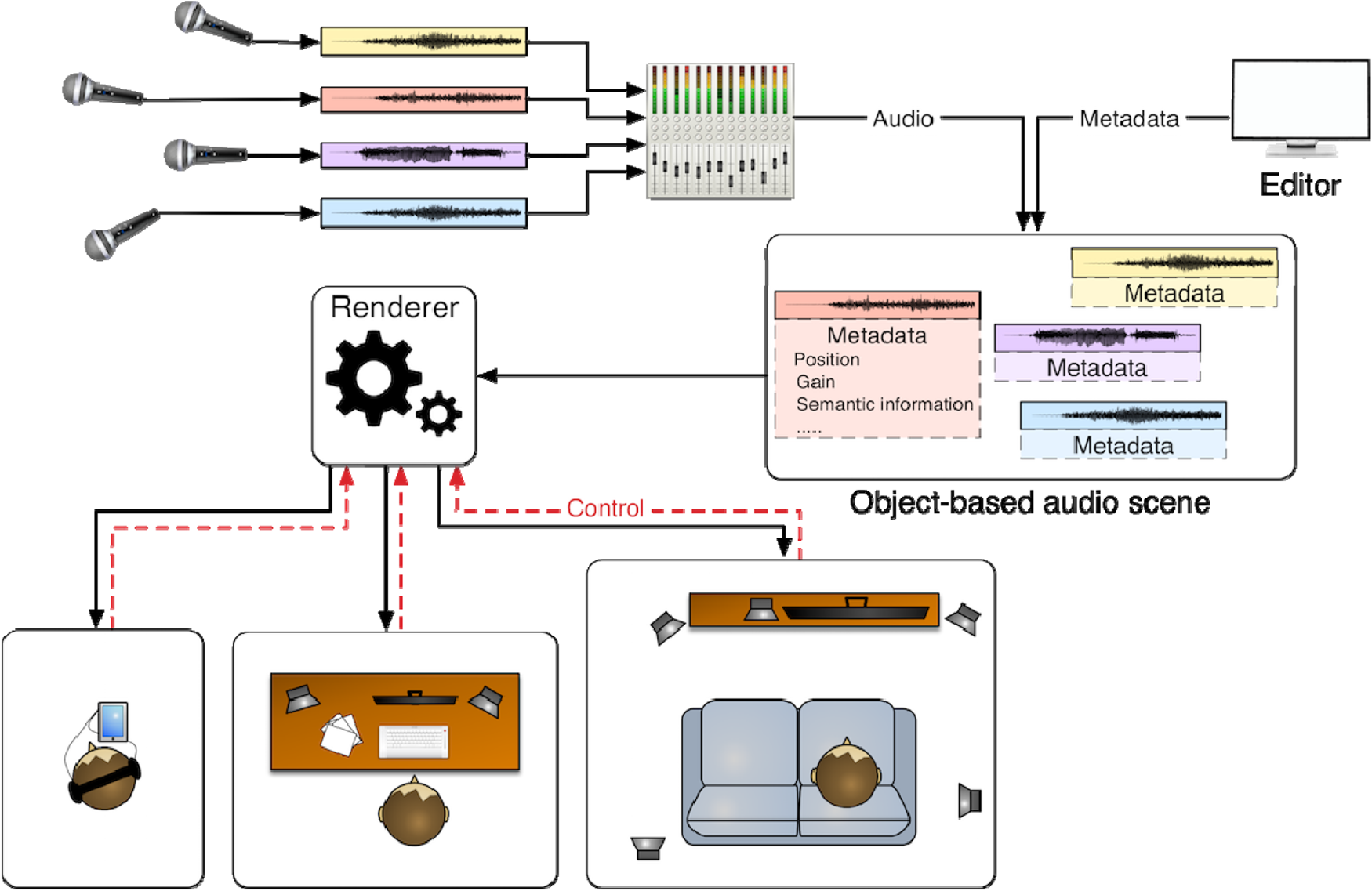
Fig. 3. Conceptual overview of object-based audio production and consumption, figure courtesy (https://lab.irt.de/demos/object-based-audio/).
Originated in game audio, object audio becomes the de facto foundation of the new immersive audio taxonomy. One of the core components of object audio is metadata. The metadata associated with each object could include many aspects but typically the target position and loudness of the audio signal [2]. The positional metadata for describing audio objects uses a Cartesian coordinate system as shown in Fig. 4. For professional audio, e.g. in the film industry, the coordinate values are normalized relative to reference points of a cube, which represents an idealized cinema model [2]. In a schematic illustration of the cinema model in Fig. 5, the front plane is the location of the screen. This metadata is transferred to the rendering side and it's up to the renderer to map the object audio position within the cube to cinema loudspeakers or other playback settings. The rendering method of object audio is generally based on panning, which is how the sound generates a certain sense of azimuth/elevation in multiple speakers or headphones through the relationship of amplitude and phase.
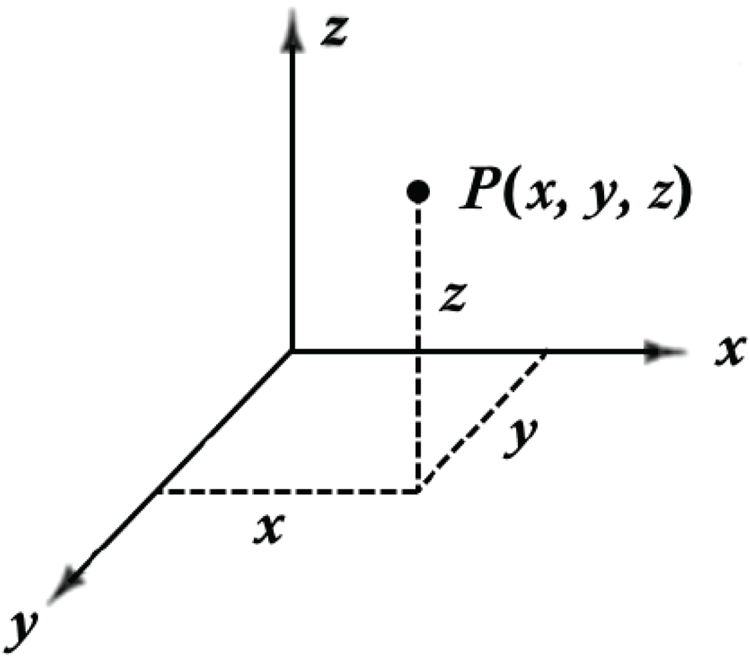
Fig. 4. Cartesian coordinate system.
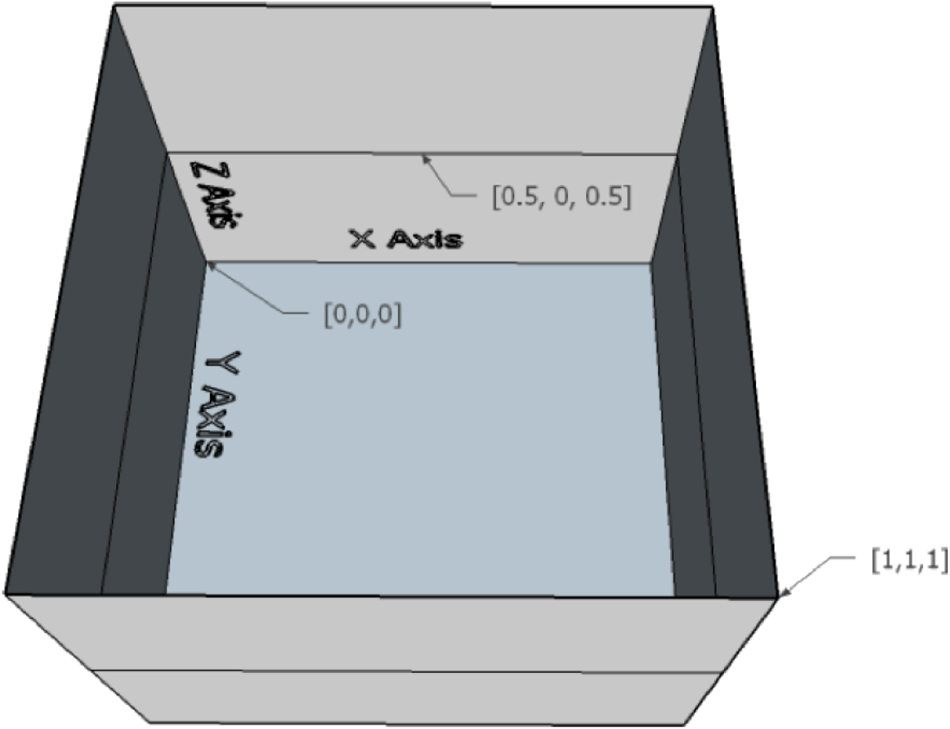
Fig. 5. Cube with example coordinates, figure courtesy [2].
D) Scene-based audio
SBA is mainly used to describe the scene of a sound field, and the core of the underlying algorithm is higher order ambisonic (HOA). The ambisonic technique was proposed by Michael Gerzon date back to 1970s [Reference Gerzon3]. Gerzon devised a mathematical framework for the capture and reproduction of immersive sound. Jérôme Daniel later extended and generalized ambisonics to HOA [Reference Daniel4]. Since then, HOA has triggered enormous interest in the academic community and audio enthusiasts. Unfortunately, practical application of ambisonic has been quite limited as it lacks commercial success when compared with 5.1 surround sound. Interestingly ambisonic was rejuvenated in the past decade, in particular with the help of VR/AR and immersive audio standards. Ambisonic describes the sound field in 3D space, for example, the first-order ambisonic (FOA), through polar coordinates. An FOA system represents a sound source with W, X, Y, Z as below (Fig. 6):

where Si represents the ith mono audio signal, Φ is the azimuthal angle in mathematical positive orientation (counter-clockwise), and θ being the elevation angle zero point to the equator and positive 90 degree to the north pole.
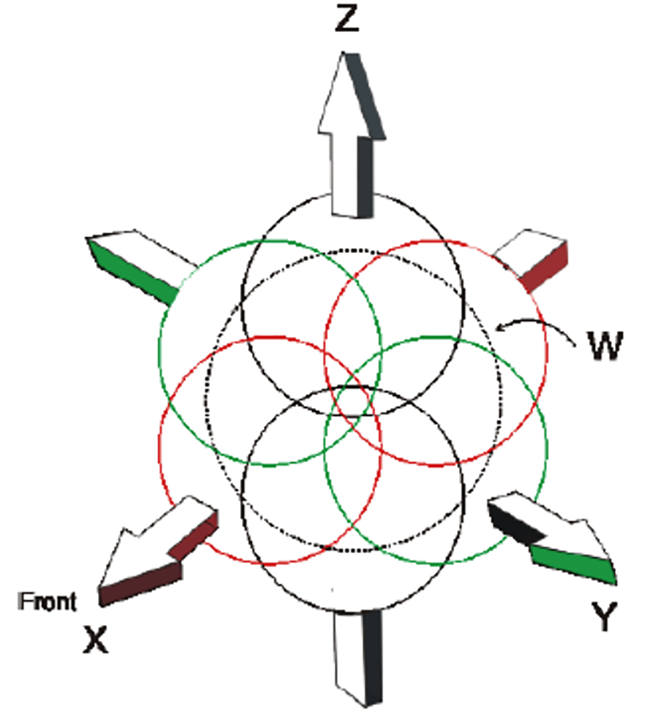
Fig. 6. Spherical coordinate system for first-order ambisonic.
W as the zero-order signal, represents an omni-directional component, whereas XYZ are the figure-of-8 directional components. This WXYZ representation is often called B-Format, conveniently linking object audio to ambisonics.
Ambisonics can also be generated by soundfield microphone arrays. Figure 7 shows a schematic representation of an FOA soundfield microphone, where LFU, LBD, RBU, RFD represent microphones pointing to Left Front Up, Left Back Down, Right Back Up, Right Front Down, respectively. This unusual arrangement of microphone capsules is known as a tetrahedral array. The raw microphone array signals are often called A format, whereas the converted signal in the spherical harmonic domain is B format as shown in equations (2) and (3). B format is an intermediate format, from which loudspeaker feed signals for various layouts can be decoded, regardless of the input soundfield capture device.

where $C = \left[ {\begin{array}{*{20}{c}} 1& 1& 1& 1\\ 1& 1& { - 1}& { - 1}\\ 1& { - 1}& 1& { - 1}\\ 1& { - 1}& { - 1}& 1 \end{array}} \right]$ .
.

Fig. 7. A schematic representation of an FOA soundfield microphone.
FOA representation of 3D space can only offer limited localization resolution, albeit being highly efficient. Fortunately, extending FOA to HOA for more accurate localization can be elegantly realized within the spherical harmonic framework.
The sound pressure field of a surround audio signal around the origin at position ($r,\theta ,\varphi$![]() ) can be described by spherical harmonic function of physics by Equations (4) and (5) below.
) can be described by spherical harmonic function of physics by Equations (4) and (5) below.
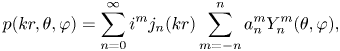
where
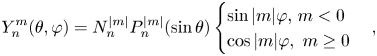
jn: spherical Bessel functions of order n
$Y_n^m$![]() : spherical Harmonic function of order n, degree m
: spherical Harmonic function of order n, degree m
$a_n^m$![]() : spherical Harmonic coefficients of order n, degree m. This is the ambisonic component corresponding to the well-known B-Format signal as in equations (1)–(3), derived by taking the so-called spherical harmonic transform (SHT) of the pressure over a sphere of radius r as shown in equation (6) [5],
: spherical Harmonic coefficients of order n, degree m. This is the ambisonic component corresponding to the well-known B-Format signal as in equations (1)–(3), derived by taking the so-called spherical harmonic transform (SHT) of the pressure over a sphere of radius r as shown in equation (6) [5],
$P_n^{|m|}$![]() : associated Legendre functions of order n, degree m,
: associated Legendre functions of order n, degree m,
$N_n^{|m|}$![]() : a normalization term $\sqrt (2 - {\delta_m})\frac{{({n - |m |} )!}}{{({n + |m |} )!}}$
: a normalization term $\sqrt (2 - {\delta_m})\frac{{({n - |m |} )!}}{{({n + |m |} )!}}$![]() ,
,
S: is the unit sphere.
The sound pressure is defined by $p(kr,\theta ,\varphi )$![]() , $k,r,\theta ,\varphi$
, $k,r,\theta ,\varphi$![]() where k is wave number, r radius, θ elevation, ϕ azimuth, respectively.
where k is wave number, r radius, θ elevation, ϕ azimuth, respectively.
Equation (5) represents the real form of spherical harmonics which is commonly used in audio signal processing. The corresponding complex form can also be found in literature, e.g. [5]. Using the orthonormality property of the spherical harmonics $Y_n^m (\theta ,\varphi )$![]() , equations (4)–(6) can be further simplified, thus establishing important relationship between the sound field pressure and spherical harmonic coefficients [5].
, equations (4)–(6) can be further simplified, thus establishing important relationship between the sound field pressure and spherical harmonic coefficients [5].
Assuming plane wave source signal s in the direction of ($\theta ,\varphi$![]() ), for example, we can derive the second-order ambisonic components as below (equation (7)), which constitutes an ambisonic encoding process expressed in general by s $Y_n^m (\theta, \varphi)$
), for example, we can derive the second-order ambisonic components as below (equation (7)), which constitutes an ambisonic encoding process expressed in general by s $Y_n^m (\theta, \varphi)$![]() . Note that new-field filters are needed for spherical waves in deriving the ambisonic components [Reference Daniel4].
. Note that new-field filters are needed for spherical waves in deriving the ambisonic components [Reference Daniel4].
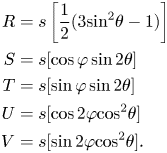
For 3D reproduction, the total number of ambisonic channels N is determined by
where M is the order of the system.
Therefore, as shown in Fig. 8, a third-order HOA system is comprised of 16 channels.
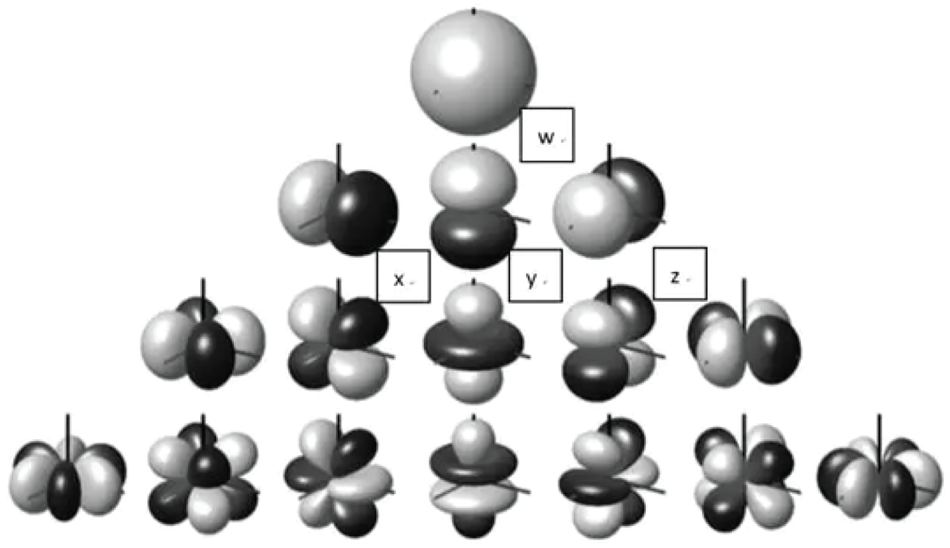
Fig. 8. Polar patterns of third-order ambisonic channels.
For horizontal-only 2D reproduction, channels depending on z-values are not counted which leads to:
One of the most attractive features of ambisonics is that the soundfield can be rotated elegantly around all three axes of a xyz coordinate system by means of simple rotation matrices. Rotation (or yaw) refers to the z-axis, tilt (or roll) to the x-, and tumble (or pitch) to the y-axis. It is also possible to apply operations like mirror and zoom to the soundfield, by the means of Lorentzian transformations or filters. Figure 9 presents a few visual illustrations of soundfield manipulation [5].
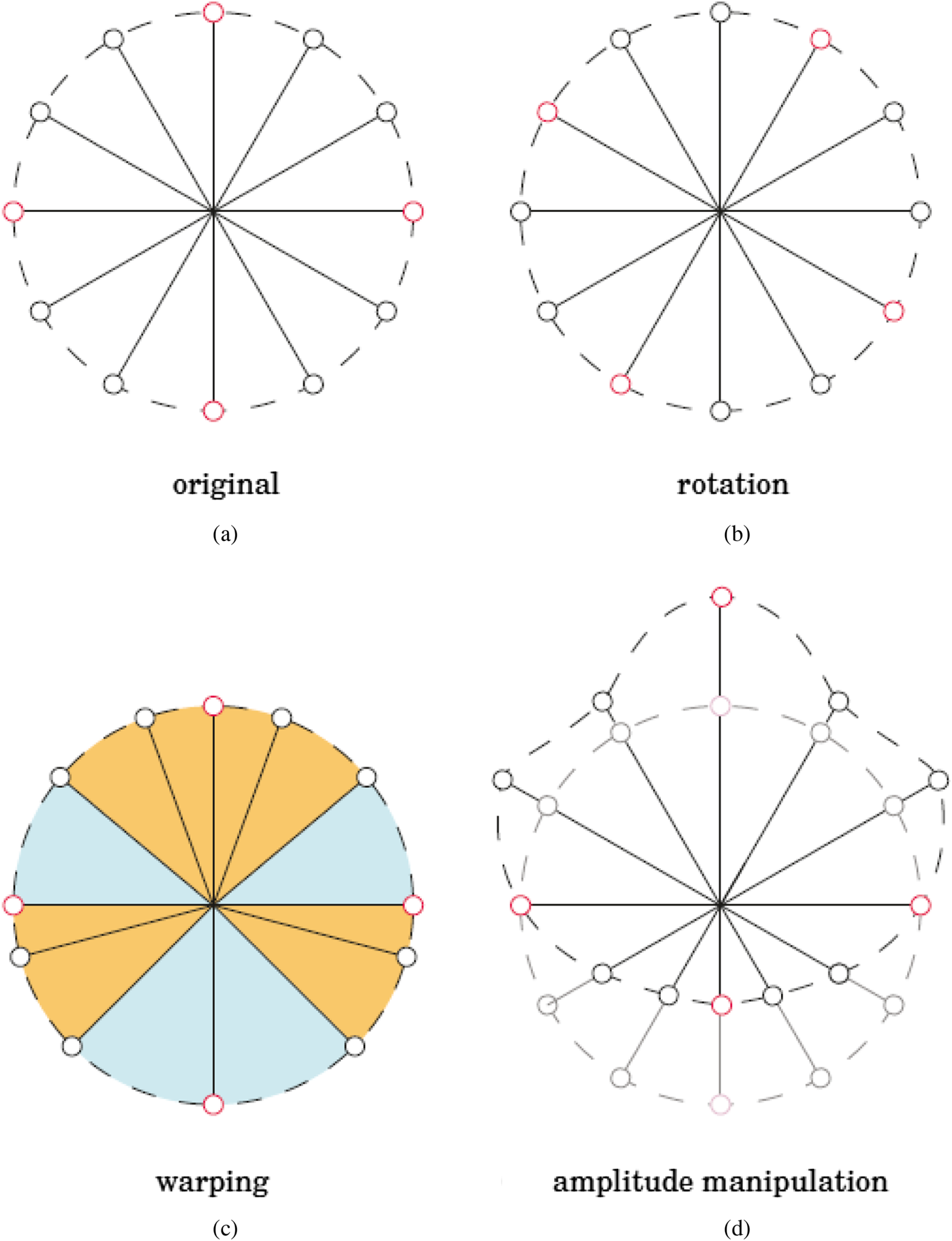
Fig. 9. Soundfield manipulation, figure courtesy Politis [5].
II. SOUND CAPTURE
A) Binaural recording
Binaural recording is a simple method for recording immersive audio, dated back to 1881. It utilizes two microphones with one in each ear, either on a “dummy head” or a real human head, and simulates the sound heard in the left/right ear. Binaural recording is for replay using headphones and would require cross talk cancellation for playback over stereo speakers (Fig. 10).

Fig. 10. 3Dio Omni Pro binaural microphone, courtesy (https://3diosound.com/).
There are various binaural recording earphones or dedicated devices, e.g. 3Dio as in the figure above (https://3diosound.com/), suitable for 360 audio recording. Even though there might be mismatch between the recording device and the listeners' own anthropomorphic properties, binaural recording often creates more compelling 3D experience than that of other soundfield capture approaches such as ambisonic. The output format of this 3Dio four-way recording is four stereo-files which represent four lines of sight at 0°, 90°, 180°, and 270°. During playback, audio signals are interpolated for angles in between these fixed numbers. This format is usually called quad binaural (QB), and had found some applications in VR content presentation. The downside of using binaural recordings is its inflexibility in post-production, which hampers its wider applications as compared with other formats.
B) Ambisonic recording
More popular soundfield recordings come from ambisonic microphones, in part because the ambisonic signal obtained by the recording device can flexibly be converted to various formats or manipulated in a lot of subsequent processing. However, if the ambisonic signal is to be converted to binaural, the quality would be subject to the performance of the binaural algorithm, which would be an approximation to the real binaural signal at best.
The author and team had made some informal perceptual comparisons between FOA and QB formats. If it is used for VR 360-degree sound field acquisition, the overall performance of FOA recording is more even regardless of the listening angle, whereas for QB, there is a distinct difference between direct captured directions versus interpolated directions.
A list of public available ambisonic microphones is compiled as below, and is by no means exhaustive.
• em32 Eigenmike (https://mhacoustics.com/products#eigenmike1)
• AMBEO VR MIC (https://en-us.sennheiser.com/microphone-3d-audio-ambeo-vr-mic)
• ZOOM H3-VR (https://www.zoom-na.com/products/field-video-recording/field-recording/zoom-h3-vr-handy-recorder)
• Zylia (https://www.zylia.co/)
• Tetra Mic (http://www.core-sound.com/TetraMic/1.php)
• Rode NT-SF1 (http://en.rode.com/nt-sf1)
• Spatial Mic (https://voyage.audio/spatialmic/)
• Twirling720 Lite (http://www.twirlingvr.com/index.php/home/lite/lite-en.html)
• VisiSonics Audio Visual Camera (https://visisonics.com/)
The algorithm of sound field acquisition and the equipment of microphone are relatively complex. In building soundfield microphones, sensors' SNR, consistency, sensitivity, and frequency response have to be carefully looked into. Electret condenser microphones (ECM) are commonly selected in the past due to higher SNR in general. In recent years, thanks to the explosive growth of speech-enabled smart devices, MEMS microphones are increasingly more popular due to their significantly improved SNR and superior consistency with regarding to sensitivity and frequency response (Fig. 11).

Fig. 11. Eigenmike from M.H. Acoustics.
In early days since 1973, soundfield microphones are predominantly first-order microphones. However, FOA only provides very coarse spatial resolution. Nowadays commercial ambisonic microphones steadily move to higher orders, e.g. OCTOMIC by Core Sound, almost second order (eight capsules), Zylia ZM1 (third order, 19 capsules), Eigenmike EM32 (fourth order, 32 capsules). There are also various reports on 64-channel microphones for supporting seventh order HOA capture (https://visisonics.com/) [Reference Kaneko6, Reference Moschner, Dziwis, Lübeck and Pörschmann7].
The array signals acquired by ambisonic sound field microphones can be approximated by spherical harmonic function of a rigid sphere, and the signals obtained by the sensors can be converted into coefficients of spherical harmonic function, and then the subsequent rotation of sound field and other operations can be carried out according to the coefficients [5, Reference Moreau, Daniel and Bertet8]. For better HOA signal estimation, it is desirable to use directional sensors to improve spherical microphone directivity. Using a diffracting structure, e.g. a rigid sphere, also help improving the directivity of continuous spherical microphones [Reference Moreau, Daniel and Bertet8].
For sound field capture using HOA microphones, adding a large numbers of sensors on a rigid sphere will inevitably increase the form factor, thus leading to new issues affecting soundfield reconstruction fidelity including spatial aliasing and white noise amplification. There are two spatial aliasing factors of concern [Reference Moreau, Daniel and Bertet8]. One is according to the sampling theorem the distance d between sensors stipulates a frequency limit above which spatial aliasing occurs and another factor of spatial aliasing stems from undersampled spherical harmonic functions (Fig. 12).
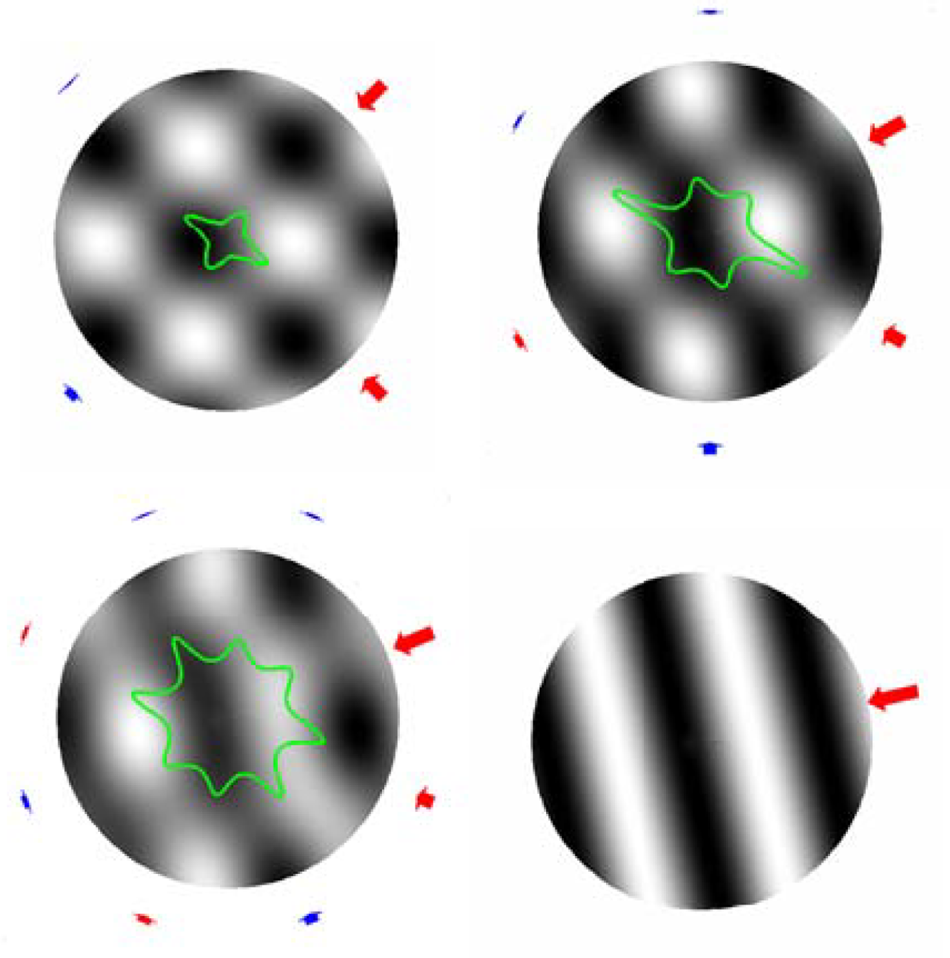
Fig. 12. Progressive plane wave reconstruction with ambisonic orders M = 1 to 3 (left to right, top to bottom). The boundary of well-reconstructed area is shown as a constant-error contour, figure courtesy [Reference Moreau, Daniel and Bertet8].
Progressive plane wave reconstruction with ambisonic orders M = 1–3 (left to right, top to bottom). The boundary of well-reconstructed area is shown as a constant-error contour, figure courtesy [Reference Moreau, Daniel and Bertet8].
By increasing the order of HOA, the area of plane wave reconstruction (i.e. the area of sweet spot) is also increased as shown in Fig. 12.
C is the sound velocity and M is the order of spherical harmonics.
If the radius of our head is r = 8.8 cm, the aliasing frequencies derived from equation (10) are listed in the table below for different ambisonic orders. In this case, the deviation of positioning accuracy is defined in Table 1
Table 1. Limit frequencies film of the acoustic reconstruction at a centered listener ears. Predicted angle αE of the blur width of the phantom image.

Many devices under test (DUTs), such as mobile phones, are smaller than the human head. The figure below demonstrates the analysis results when the radius is smaller than that of the head (4.2 cm), using a 32-channel array (fourth-order HOA). It can be seen that when increasing the number of microphones and the order of spherical harmonics, we inevitably have to face the dilemma of enhancing the weak high-order components and amplifying the background noise Fig. 13.
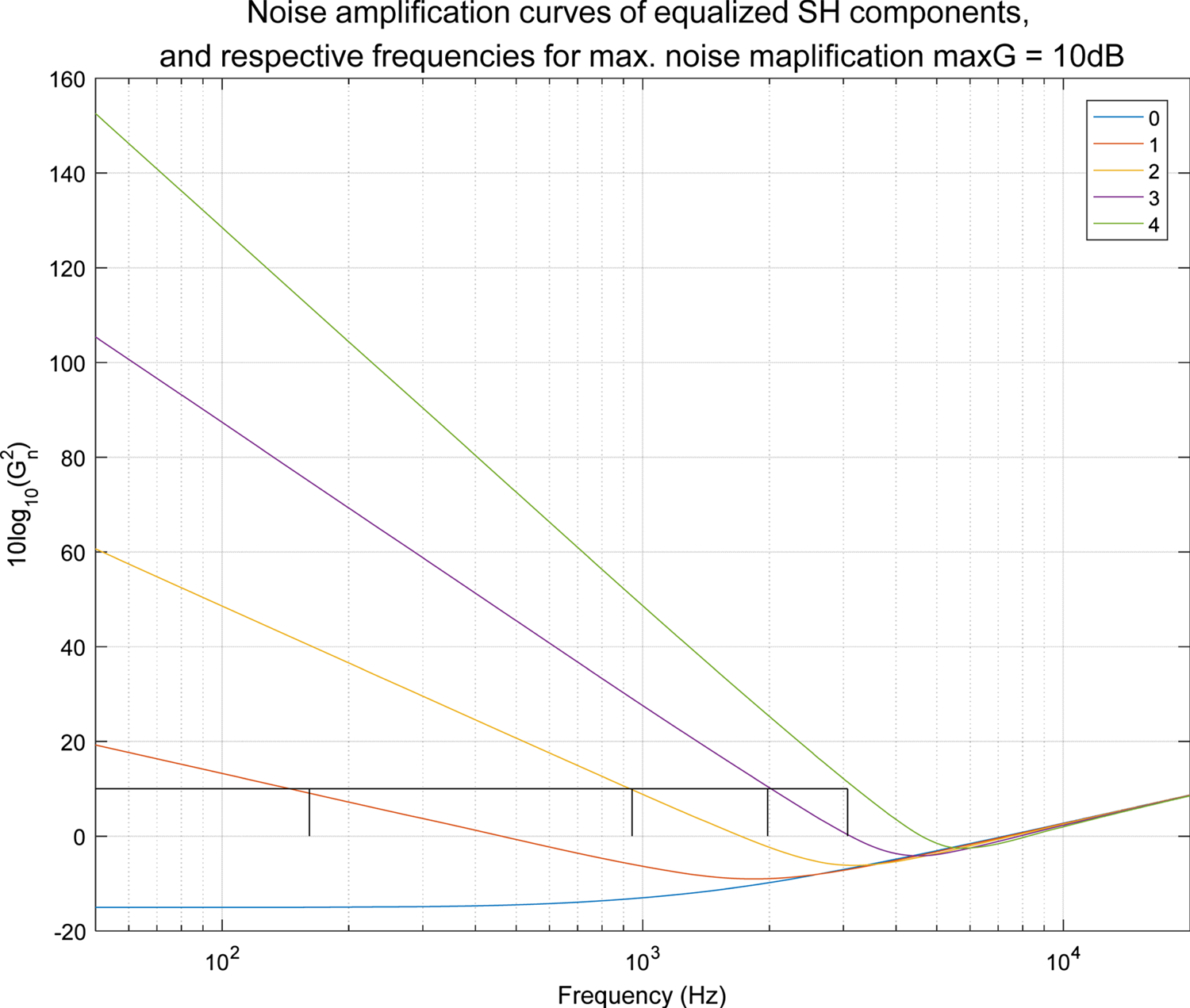
Fig. 13. Noise amplification curves for different HOA orders (http://research.spa.aalto.fi/projects/spharrayproc-lib/spharrayproc.html).
It is conventionally to use normalized mean square error or normalized reconstruction error to describe the objective accuracy of sound field reconstruction [Reference Moreau, Daniel and Bertet8].
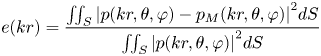
k is the wavenumber and r is the radius of the ball, S is the unit sphere.
Equation (12) shows the reconstruction error is a function of kr, where $p(kr,\theta ,\varphi )$![]() represents the original soundfield, and ${p_M}(kr,\theta ,\varphi )$
represents the original soundfield, and ${p_M}(kr,\theta ,\varphi )$![]() is the soundfield truncated up to order M in practice. This function represents the distance to the center of the array and is frequency-dependent. For a specific kr value, if the distance increases, the frequency decreases (i.e., the wavelength becomes longer). So the sweet spot is bigger for lower frequencies (Fig. 14).
is the soundfield truncated up to order M in practice. This function represents the distance to the center of the array and is frequency-dependent. For a specific kr value, if the distance increases, the frequency decreases (i.e., the wavelength becomes longer). So the sweet spot is bigger for lower frequencies (Fig. 14).
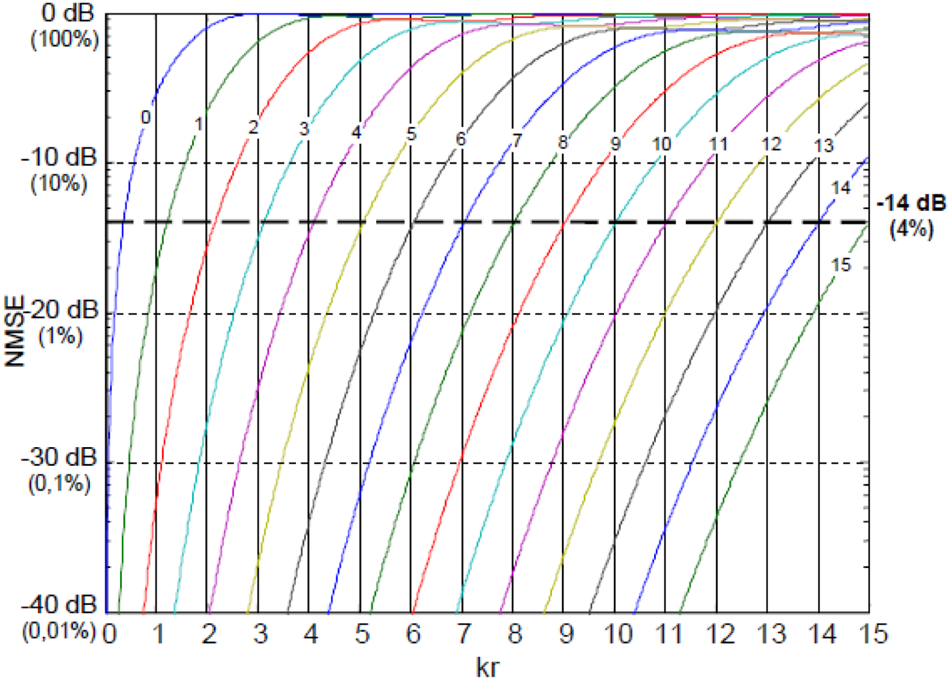
Fig. 14. Mean square error of plane wave reconstruction, courtesy [Reference Moreau, Daniel and Bertet8].
The above figure describes the mean square error of plane wave reconstruction. The x-axis is radial distance kr, and different curves represent different orders of spherical harmonics. Using the mean square error of 4% as the threshold, a simple rule for estimating HOA order to meet the reconstruction accuracy is
For example, for reproducing 1 kHz plane wave field in a 0.1 m sphere (allowing 4% error), we will need second-order spherical harmonics. For 5 kHz, at least ninth-order spherical harmonics are required Table 2.
Table 2. A comparison of HOA microphones.
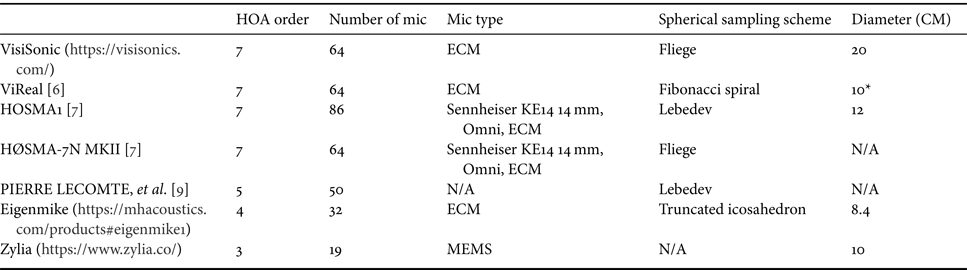
*The number is based on the simulation microphone described in [Reference Kaneko6]. It's not clear if the real microphone also uses the same size.
Due to the inevitable discretization process in practical spherical microphone or loudspeaker arrays, the sensor arrangement or the spatial sampling scheme is of critical importance to preserve the orthonormality criterion of $Y_n^m (\theta , \varphi)$![]() in order to avoid aliasing between spherical harmonics orders [Reference Moreau, Daniel and Bertet8, Reference Lecomte, Gauthier, Langrenne, Berry and Garcia9]. In the discrete version, the acoustic signal picked up by each sensor on a spherical surface of radius R can be expressed by equation (4) by replacing the radial function jn with
in order to avoid aliasing between spherical harmonics orders [Reference Moreau, Daniel and Bertet8, Reference Lecomte, Gauthier, Langrenne, Berry and Garcia9]. In the discrete version, the acoustic signal picked up by each sensor on a spherical surface of radius R can be expressed by equation (4) by replacing the radial function jn with
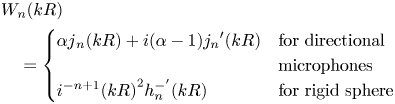
where ${j_n}^{\prime}(kR)$![]() is the first derivative of ${j_n}(kR)$
is the first derivative of ${j_n}(kR)$![]() , $h_n^ - (kR)$
, $h_n^ - (kR)$![]() and $h_n^{ - ^{\prime}}(kR)$
and $h_n^{ - ^{\prime}}(kR)$![]() are the Hankel function and its first derivative according to kR, respectively [Reference Moreau, Daniel and Bertet8]. Such a theoretical encoding approach is applicable for spherical arrays with uniform or nearly-uniform sensors arrangement. For arbitrary array shapes and unconventional arrangements, encoding matrix can be obtained through impulse response measurements [5].
are the Hankel function and its first derivative according to kR, respectively [Reference Moreau, Daniel and Bertet8]. Such a theoretical encoding approach is applicable for spherical arrays with uniform or nearly-uniform sensors arrangement. For arbitrary array shapes and unconventional arrangements, encoding matrix can be obtained through impulse response measurements [5].
Various sampling schemes were proposed in the literature in order to fulfil the orthonormality criterion, thus avoiding aliasing errors. Equiangular sampling exhibits equal spacing between the sampling points in both azimuthal and elevation planes [Reference Moreau, Daniel and Bertet8]. But they suffer from dense sampling points at the poles. Both VisiSonic and HØSMA-7N MKII adopt a Fliege grid design. Lecomte et al. [Reference Lecomte, Gauthier, Langrenne, Berry and Garcia9] demonstrate that comparing a 50-node Lebedev grid with a Fliege and a T-design grid that both use almost the same number of nodes, the Lebedev grid yields the best performance in terms of sound field capture and reproduction. It exhibits better orthogonality among spherical harmonic vectors as compared to T-designs and Fliege nodes. ViReal [Reference Kaneko6] emphasizes that the strength of a Fibonacci spiral (FS) configuration is flexibility in terms of the choice of the number of microphone capsules. Fibonacci sampling exhibits nearly uniform sampling on a sphere with closed form expression for angular directions for any number of sampling points.
C) Distributed recording
Recent years have seen some popularity of distributed recording of soundfield using multiple FOA or HOA microphones [Reference Lee10–Reference Tylka and Choueiri12].
As evident in previous discussion, coincident FOA microphones only offer limited spatial resolution and the perceived spaciousness and the size of the sweet spot in loudspeaker reproduction are also limited due to the high level of interchannel correlation. HOA microphones provide higher spatial resolution and larger sweet spot, at the cost of more complex design and construction.
On the other hand, a near-coincident or distributed microphone array can provide a greater balance between spaciousness and localizability, due to the availability of both interchannel time difference and level difference.
Lee [Reference Lee10] proposes to use a quadraphonic equal segment microphone array (ESMA) to capture a 360° soundfield, where four cardioid microphones with spacing of 0, 24, 30, and 50 cm were investigated. The results show 50 cm spacing produced the most accurate localization (Fig. 15).
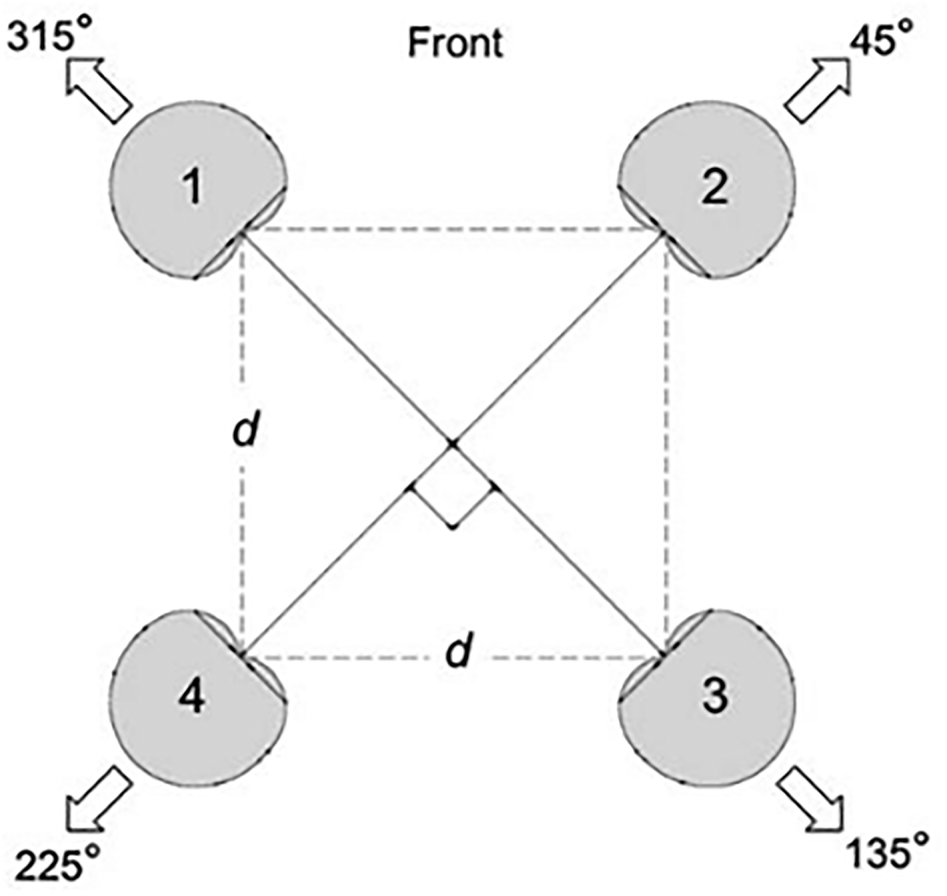
Fig. 15. Equal segment microphone array (ESMA), courtesy Lee [Reference Lee10].
Bates et al. [Reference Bates, O'Dwyer, Flachsbarth and Boland11] utilizes four FOA microphones with a 50 cm spacing, demonstrated that six degrees of freedom (6DOF) needed in a VR application can be realized by such recording arrangement.
It is reported that Zylia built a test setup consisting of 53, third-order ambisonic microphone arrays in five layers (https://www.provideocoalition.com/zylia-introduces-53-microphones-installation-for-virtual-reality-projects/). Microphones were connected with USB cables to a laptop to create soundfield with 6DOF. Considering each Zylia microphone is built with 19 digital MEMS, it's a whopping 1007 channels of microphone signals in total for such a setup.
D) Production and content creation
Support of immersive audio among popular professional DAWs has been growing steadily. The mainstream packages such as Pro Tools, Reaper and Nuendo are commonly used in the film and television industry, all have integrated object audio and HOA into their content production workflow.
Pro Tools, arguably the most commonly used DAW in the professional audio community, has fully embraced Dolby Atmos (https://www.avid.com/immersive-audio). Dolby Atmos's mixing interface, shown in the figure below, is a box that mimics a movie theater, with the screen in front. The ball represents an audio object that has a trajectory in three dimensions. The mixing engineer will wear headphones or experience the track of the remix (audio object) through his own remix environment (Fig. 16).
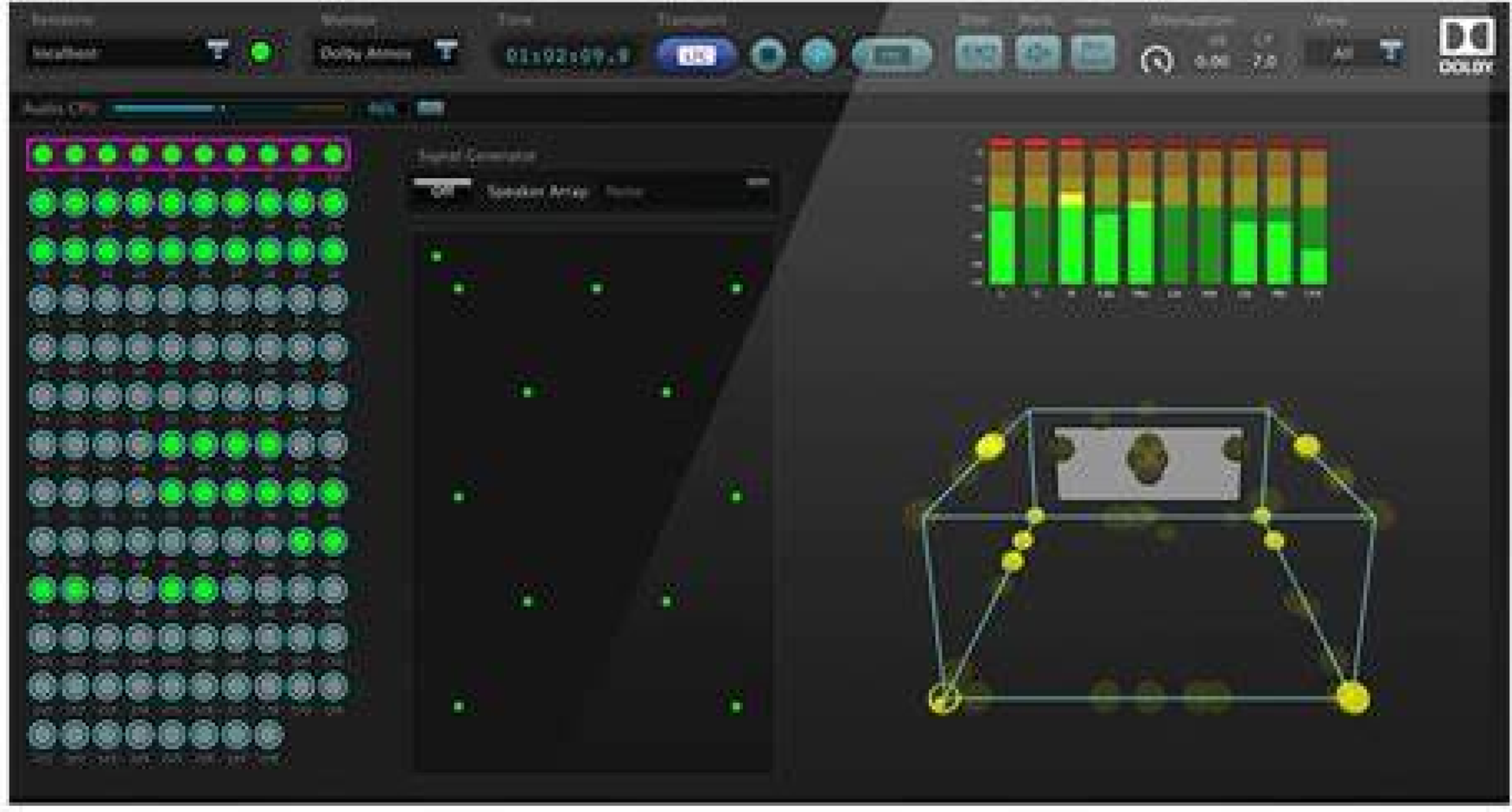
Fig. 16. Dolby Atmos mixing interface.
While object audio in game audio engines is ubiquitous, HOA support in game content creation only becomes a reality in the past few years thanks to the rise of VR games. For example, the popular middleware Wwise now supports ambisonic output up to fifth-order (36 channels) (https://www.audiokinetic.com/library/edge/?=Help&id=using_ambisonics).
There is a vast selection of plugins for object audio and HOA mixing available, e.g. [Reference McCormack and Politis13] (https://plugins.iem.at/). A detailed description of the plugins and their applications to immersive audio content creation is beyond the scope of this review. Interested readers are suggested to look into the respective DAWs for more information.
III. STORAGE AND TRANSMISSION OF IMMERSIVE AUDIO
A) Fundamentals of multichannel audio compression
Conventional multichannel audio compression is generally based on the extraction of some interchannel parameters such as phase difference and amplitude difference, on top of the mono-channel audio compression techniques. Further processing includes various ways of dimensionality reduction or decorrelation.
Early techniques such as Parametric Stereo (PS) coding compress a stereo audio signal as a monaural signal plus a small amount of spatial side information [Reference Breebaart, Van De Par, Kohlrausch and Schuijers14]. Extensive psychoacoustic research has been conducted in the past to study how humans perceive sound source location. It is generally agreed that sound source localization is facilitated by interaural intensity differences (IIDs) at high frequencies and by interaural time differences (ITDs) at low frequencies. The third parameter is coherence, which describes the sensitivity of human listeners to time-varying changes in binaural cues, often manifested perceptually as “spatial diffuseness”, and also responsible for the well-known phenomenon of binaural masking level difference.
For extracting the above three spatial parameters from multichannel signals, interchannel intensity difference (IID), interchannel phase difference (IPD), interchannel coherence (IC) are defined below, respectively [Reference Breebaart, Van De Par, Kohlrausch and Schuijers14].
For each frequency band b,
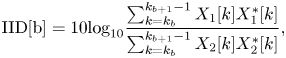
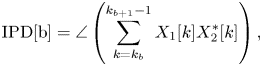
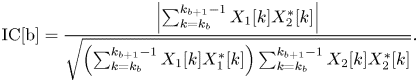
Multichannel audio compression beyond stereo signals, e.g. MPEG Surround [Reference Breebaart, Hotho, Koppens, Schuijers, Oomen and van de Par15, Reference Herre16], employs a tree structure built upon a few elementary building blocks, referred to as two-to-one (TTO), three-to-two (TTT) for encoding. The corresponding decoding blocks are one-to-two (OTT), two-to-three (TTT), respectively. The following figure describes the most commonly used 5.1 encoding structure (Fig. 17).
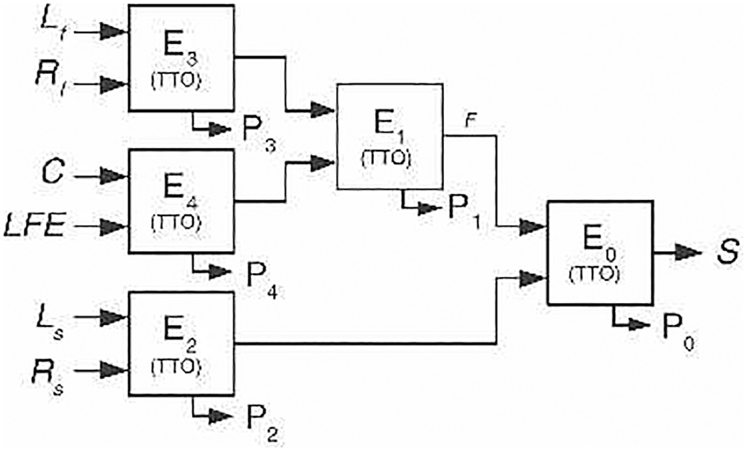
Fig. 17. 5.1 encoding structure, courtesy Breebaart et al. [Reference Breebaart, Hotho, Koppens, Schuijers, Oomen and van de Par15, Reference Herre16].
Alternative compression approaches using dimensionality reduction techniques such as KLT has been explored by [Reference Yang, Ai, Kyriakakis and Kuo17] (Fig. 18).
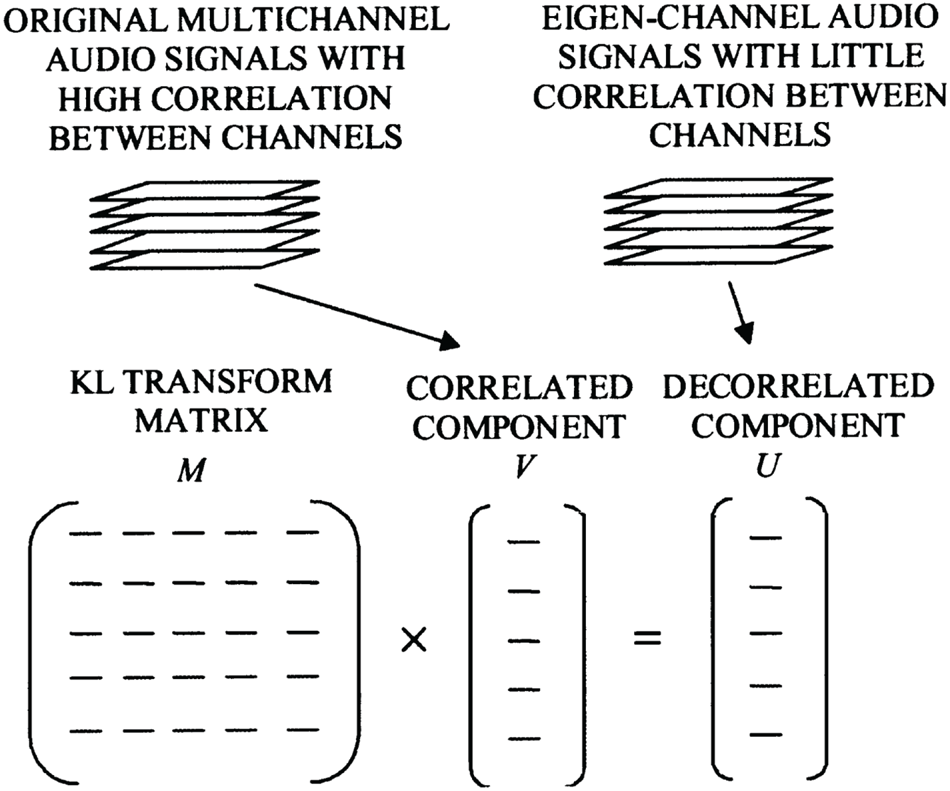
Fig. 18. Multichannel compression based on KLT transform, courtesy Dai [Reference Yang, Ai, Kyriakakis and Kuo17].
There have been a few systems aiming at ambisonic, in particular, FOA.
Chen et al. proposed a Spatially Squeezed Surround Audio Coding (S3AC) scheme for ITU 5.1 multichannel audio and ambisonic audio recordings [Reference Cheng, Ritz and Burnett18]. Instead of deriving relationships between individual channels, S3AC analyzes the localized soundfield sources and “squeezing” them into a stereo space. It's been demonstrated that a compressed (squeezed) stereo sound field was able to carry the perceptual localization information of a 360° horizontal sound scene without side information (Fig. 19).

Fig. 19. Spatially Squeezed Surround Audio Coding, courtesy Cheng et al. [Reference Cheng, Ritz and Burnett18].
Assuming each frequency bin contains just one virtual source, the corresponding azimuth for 5.1 channel-based signals is estimated by using an inverse amplitude panning law on the loudspeaker signal energy, given by:
where k is frequency index and ȥ 12 is the azimuth separation between the two speakers.
For ambisonics, the azimuth is estimated via trigonometric relationships among different ambisonic channels as described above.
Encoding is achieved by a linear azimuth mapping that re-pans each frequency-dependent source from the (e.g. 5 channel in 5.1) 360° surround soundfield into a (stereo) 60° squeezed soundfield.
Pulkki [Reference Pulkki19] (http://legacy.spa.aalto.fi/research/cat/DirAC/) proposes Directional Audio Coding (DirAC) for spatial sound reproduction in a series papers, in particular for ambisonic signals. DirAC shares many processing principles with existing spatial audio technologies in the coding of multichannel audio, however a difference is that DirAC is also applicable for recording real spatial sound environments. The processing can be divided into three steps (http://legacy.spa.aalto.fi/research/cat/DirAC/):
Analysis: the sound signals are transformed into frequency domain, and then the diffuseness and direction of arrival of sound at each frequency band are analyzed for each time frame.
Transmission: depending on quality requirement or transmission bandwidth, a mono or multichannel signals are transmitted with directional information.
Synthesis: the sound at each frequency channel is first divided into diffuse and non-diffuse streams. The diffuse stream is then produced using a method which produces maximally diffuse perception of sound, and non-diffuse stream is produced with a technique generating point-like perception of sound source.
B) MPEG-H
The core of the MPEG-H 3D [Reference Herre, Hilpert, Kuntz and Plogsties20, Reference Fug and Kuntz21] is a perceptual codec for compression of the different input signal classes: channels, objects, and HOA, based on MPEG Unified Speech and Audio Coding (USAC). As shown in the figure below, the MPEG-H bitstream is first decoded by an extended USAC module (USAC-3D). Then channel signals, objects, and HOA coefficients are decoded and rendered through respected renderers to the target reproduction loudspeaker setup (Fig. 20).
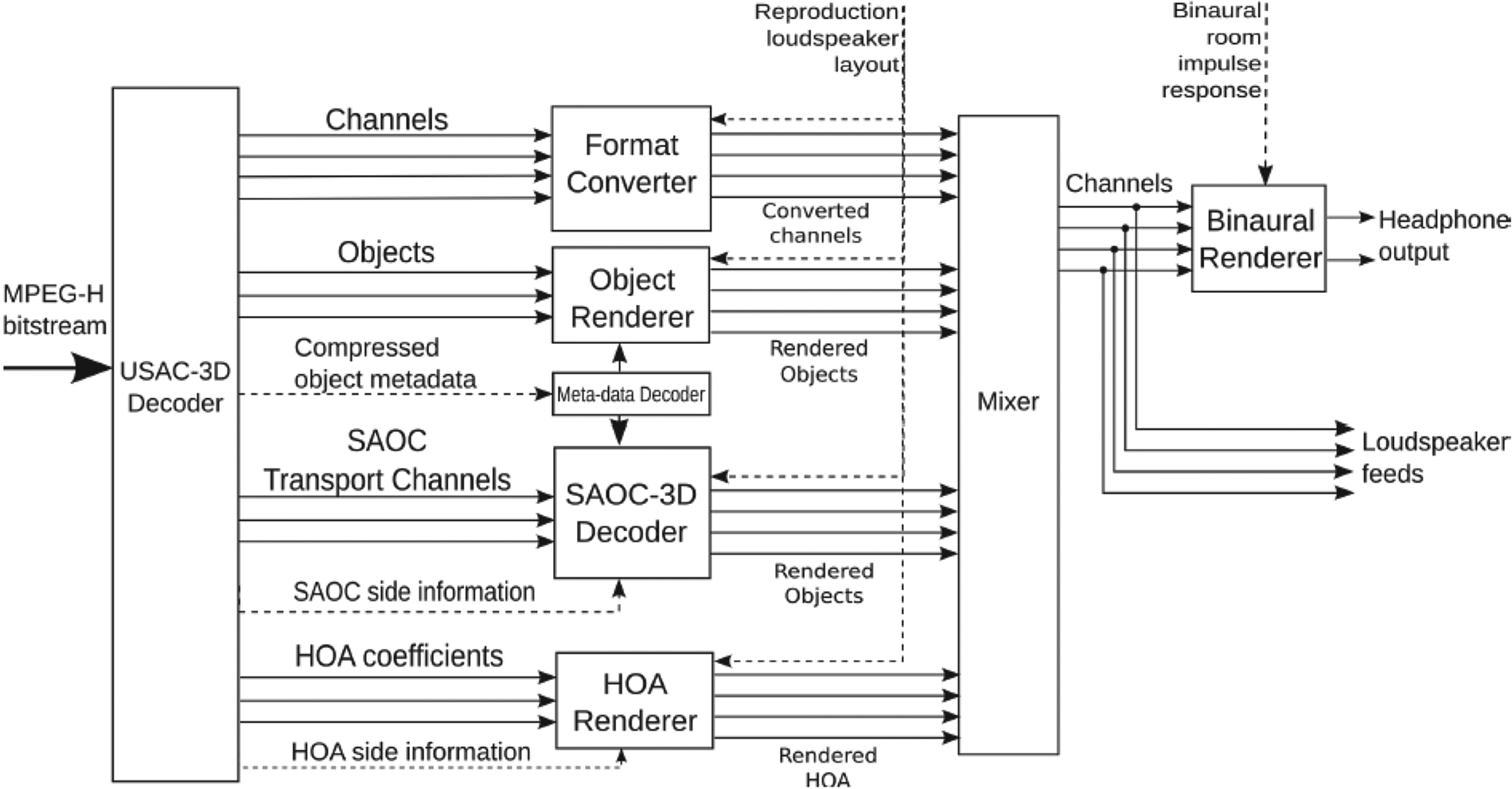
Fig. 20. MPEG-H decoding structure, courtesy Herre et al. [Reference Fug and Kuntz21].
For channel-based content, a “format converter” module maps the channel signals to various target loudspeaker setups. The core of the format converter contains two major building blocks for deriving optimized downmix matrices, a rule-based initialization block, and the active downmix algorithm.
The rendering of audio objects is realized by VBAP [Reference Pulkki22], where imaginary loudspeakers extend loudspeaker setup in regions with no physical loudspeaker presence. These virtual signals are later downmixed to the physically existing loudspeakers.
As shown in Fig. 21 below, in the HOA encoding/decoding and rendering, MPEG-H applies a two-stage coding/decoding process to improve coding efficiency [Reference Sen, Peters, Young Kim and Morrell23]. The soundfield content is decomposed into predominant (mostly directional sounds) and ambient components (mainly non-directional sounds), then the associated time-varying parameters (e.g. direction of the directional components) are transmitted together with the components. Note that the non-directional components are transmitted with reduced resolution as its details are considered less important perceptually (Fig. 22).
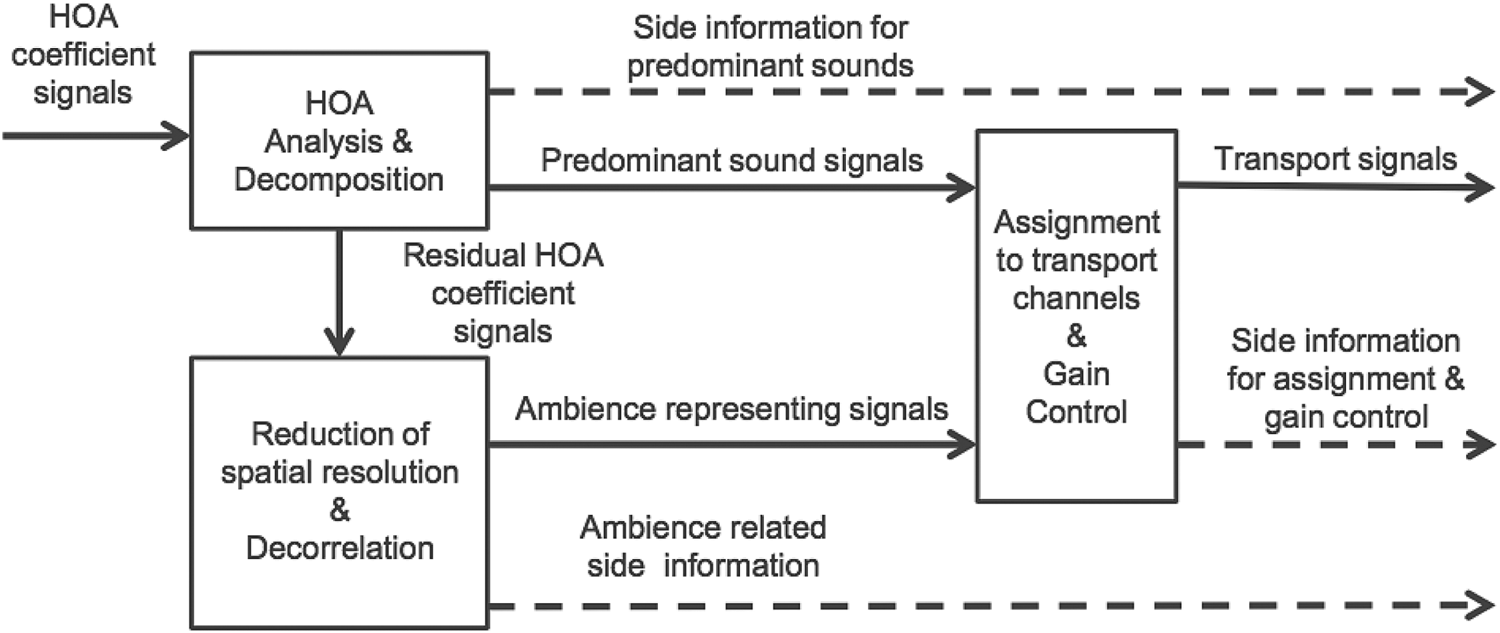
Fig. 21. MPEG-H HOA encoding structure, courtesy Sen et al. [Reference Sen, Peters, Young Kim and Morrell23].
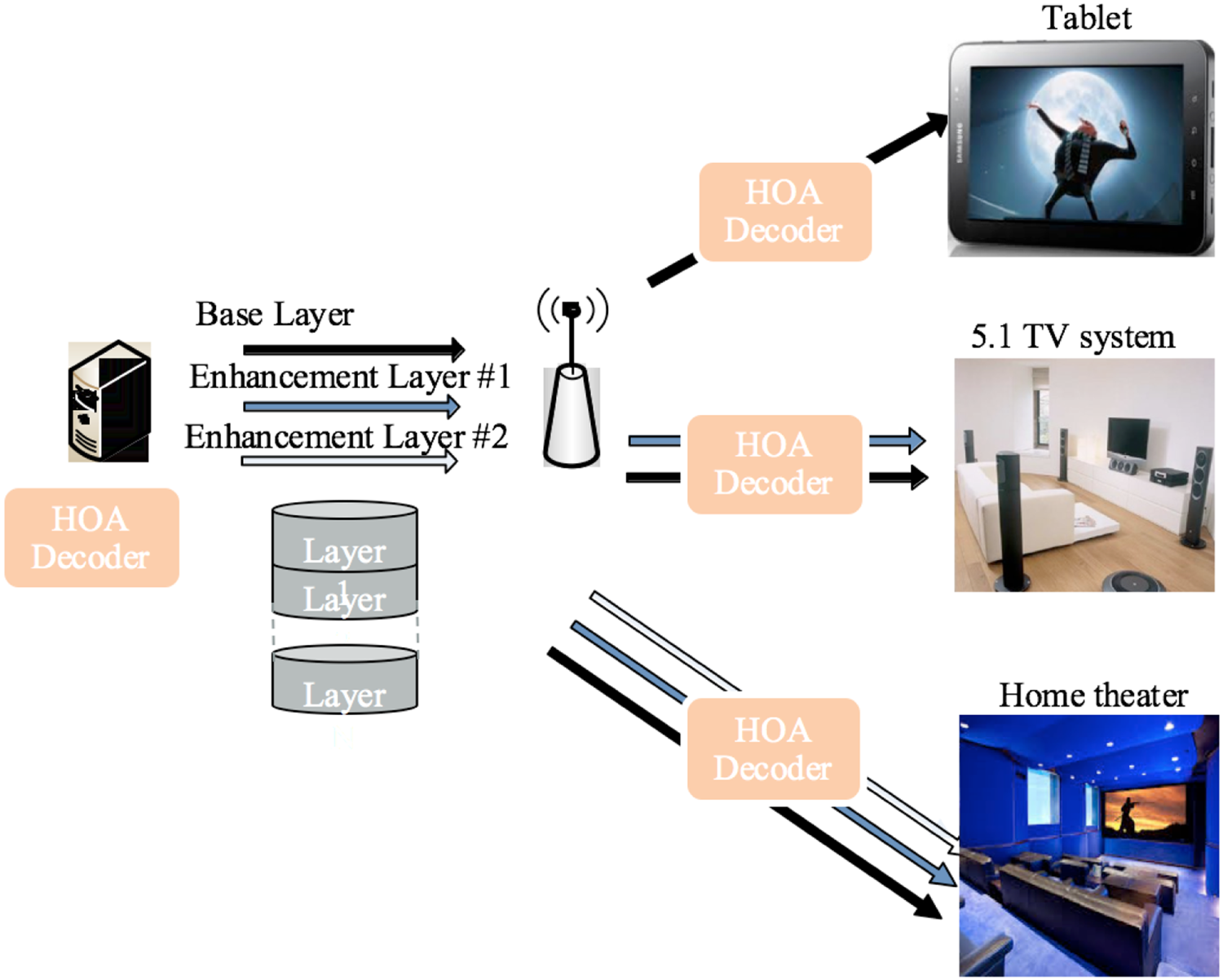
Fig. 22. MPEG-H HOA layered decoding, courtesy Sen et al. [Reference Sen, Peters, Young Kim and Morrell23].
The advantage of HOA is that there is a hierarchical coding mechanism [Reference Sen, Peters, Young Kim and Morrell23]. If the bandwidth is limited, the low-order signal with less input can be transmitted. When more bandwidth is available, the higher-order signals can be transmitted accordingly.
C) Dolby Atmos
Dolby Atmos is predominantly an object-based system, but is also designed to be compatible with legacy channel-based system, as shown in the figure below (Fig. 23).

Fig. 23. Dolby Atmos overview, courtesy Dolby (https://professional.dolby.com/content-creation/dolby-atmos/2).
Due to the large amount of audio objects as well as the need for backward compatibility, the encoding process employs a few new techniques in addition to previously mentioned multichannel compression algorithms. Firstly, joint object coding (JOC), shown in Fig. 24, was developed for compatibility with 5.1, which can reduce the immersive audio content to 5.1 downmix plus JOC parameters [Reference Purnhagen, Hirvonen, Villemoes, Samuelsson and Klejsa24]. The generated downmix signal can be well compatible with a 5.1 decoder. If object audio is supported, JOC parameters can be extracted to restore audio objects for Dolby Atmos immersive audio. In order to further reduce the bandwidth of OBA content, [Reference Breebaart, Cengarle, Lu, Mateos, Purnhagen and Tsingos25] proposes a spatial coding scheme that performs dynamic object-grouping, which represents a complex object-based scene as an equivalent reduced set of object groups. They demonstrate that a 10:1 reduction in object count can be achieved while maintaining high-quality audio playback and rendering flexibility at the endpoint. It can be further combined with audio coding tools to deliver OBA content at low bit rates. Figure 25 illustrates spatial coding process and how it is combined with JOC encoder.
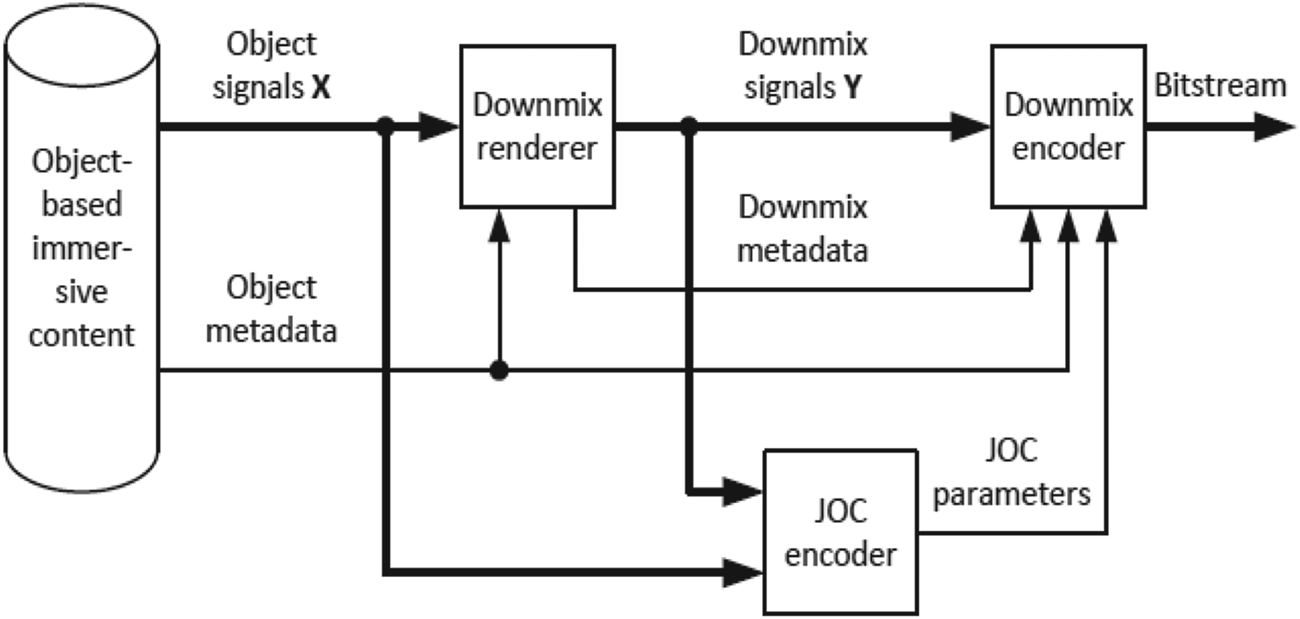
Fig. 24. Joint object coding, courtesy Purnhagen et al. [Reference Purnhagen, Hirvonen, Villemoes, Samuelsson and Klejsa24].
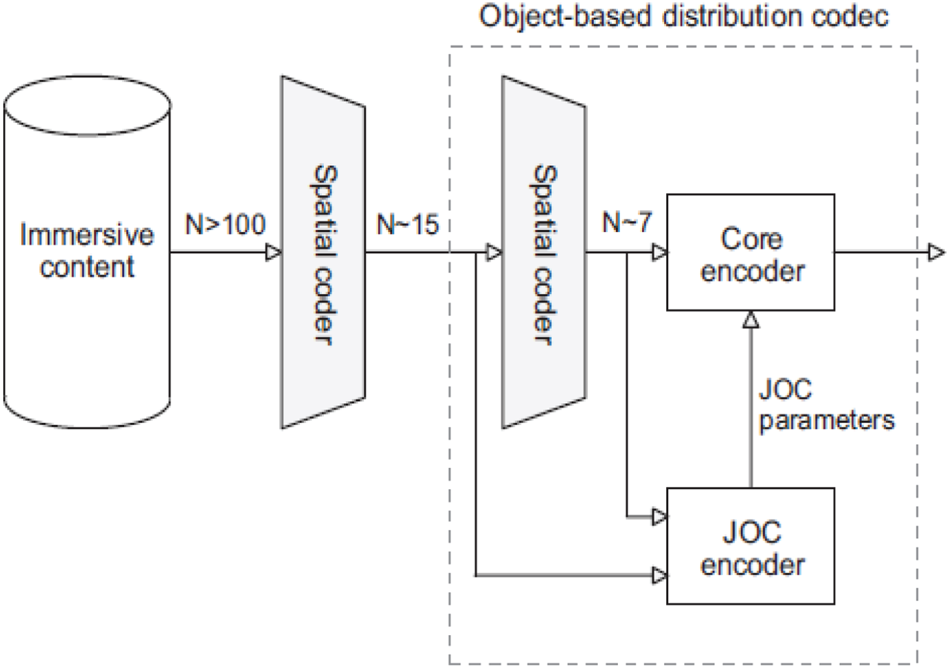
Fig. 25. Spatial coding of object audio, courtesy Breebaart et al. [Reference Breebaart, Cengarle, Lu, Mateos, Purnhagen and Tsingos25].
The core of Dolby Atmos is Dolby AC-4 codec [Reference Kjorling26] that combines high-efficiency audio coding, a transport syntax, and system-level features, utilizes two different modified discrete cosine transform frontends to code the audio. For general audio content, the Audio Spectral Frontend (ASF) is used. Dolby AC-4 also contains a dedicated Speech Spectral Frontend (SSF). This prediction-based speech coding tool achieves very low data rates for speech content. One important feature of AC-4 is Dialog Enhancement. This end-to-end feature with scalable bitrates for side-information enables the user to adjust the relative level of the dialogue to their preference. Among other features include video frame synchronous coding, dynamic range control, loudness management, hybrid delivery over both broadcast and broadband connections, and Extensible Metadata Delivery Format (EMDF) syntactical elements for additional metadata information.
D) SMPTE 2098
SMPTE has published a series of documents aiming at standardizing immersive audio, particularly the ST 2098 suite [27]. For example, ST 2098-1 defines immersive audio metadata; 2098-2, the main document, is the Immersive Audio Bitstream (IAB) specification. 2098-5 defines digital cinema immersive audio channels and soundfield group. The standard is largely based on Dolby Atmos format, yet is designed to be extensible and backward compatible. Interoperability tests among major immersive audio systems (Dolby ATMOS, Barco Auromax, and DTS:X) have already been conducted with success. Some basic concepts and definitions in SMPTE 2098 include
Audio Channel – Distinct collection of sequenced audio samples that are intended for delivery to a single loudspeaker, loudspeaker array or other reproduction device.
Audio Object – Segment of audio essence with associated metadata describing positional and other properties which may vary with time.
Soundfield Group – Collection of Audio Channels meant to be played out simultaneously through a given Soundfield Configuration.
Target Environment Specific set of conditions that is present in the playback environment.
Bed – (a.k.a. Immersive Audio Bed) – A Soundfield Group, such as a 5.1, 7.1 or 9.1, that is typically present for the duration of the program and serves as the foundation of the immersive soundtrack mix. (Channels in immersive audio are always within a Bed.)
ST 2098 also defines Base Layer, used by standard Surround Sound, while Immersive Sound uses the Base Layer and additional (typically height) layers or speakers. Note that Immersive Audio does not have to use Audio Objects.
The key element in the bitstream specification is the IAFrame (Immersive Audio Frame).
• ST 2098-2 specifies a single IAFrame without constraint on adjacent bitstream frame content
• Each IAFrame is independently decodable
• Applications can constrain bitstreams to contain IAFrames with consistent parameters
All bitstream elements are based on the following basic structure:
• ElementID – Identifies the element and its syntax. Decoders may skip unrecognized IDs
• ElementSize – Can be used to skip an unknown element
• The combination of these two items allows extensibility
By encoding bitstreams in accordance with ST 2098-2 specification, an immersive audio file can be distributed in SMPTE-compliant audio processing eco-systems. The ultimate playback experience depends on the proprietary renderer used by the theater to decode the bitstream (Fig. 26).
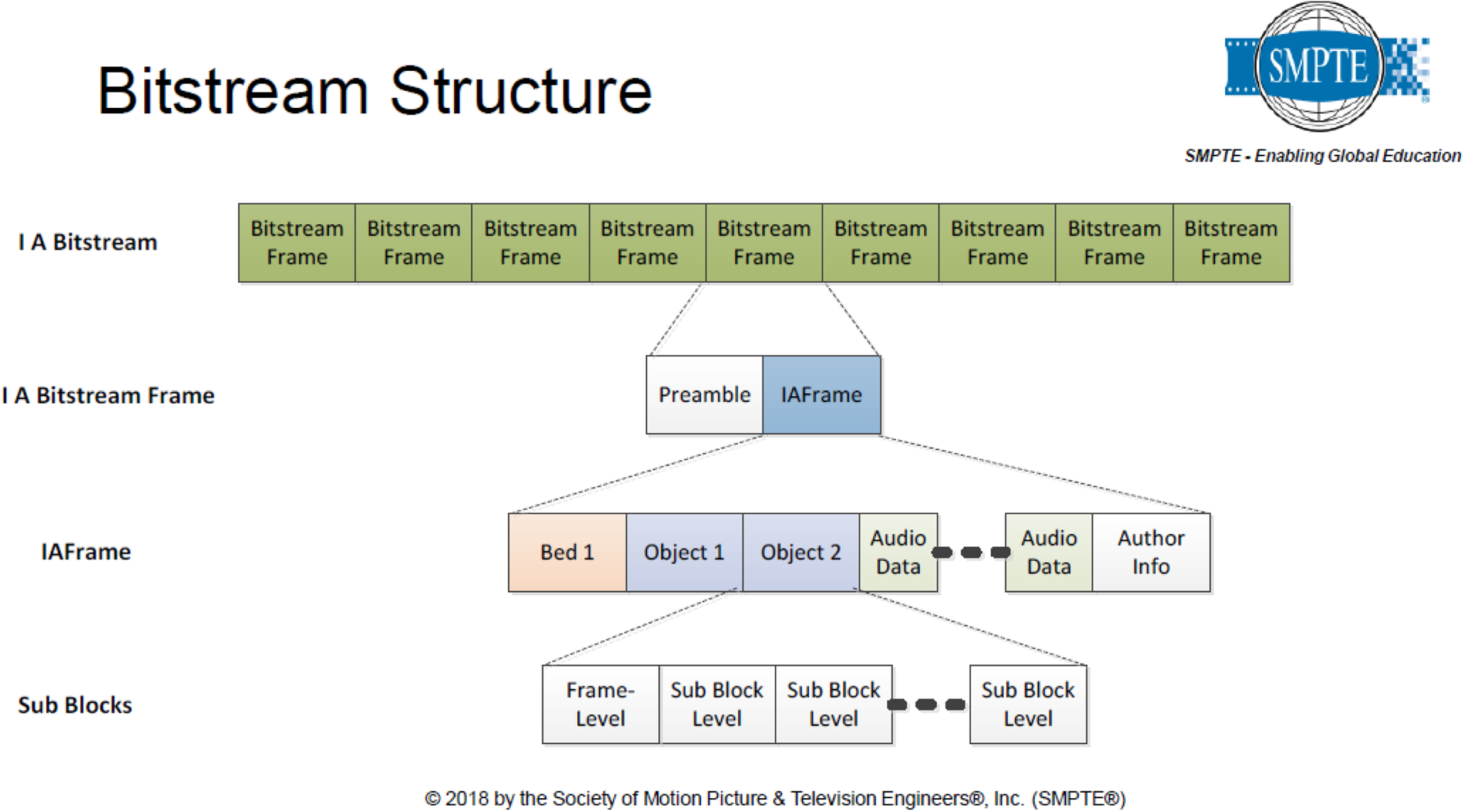
Fig. 26. SMPTE 2098 bitstream, courtesy SMPTE [27].
IV. RENDERING
A) Object audio
An object audio renderer is significantly more complex than that of a conventional channel-based renderer. That being said, the basic underlying principle remains the same, i.e. through panning. Panning in 3D space is realized via Vector-Based Amplitude Panning (VBAP) [Reference Pulkki22].
Pukki's seminal work on VBAP lays the foundation of a large amount of work on object rendering in the following years. The VBAP technology is an efficient extension of stereophonic amplitude panning techniques, for positioning virtual sources to arbitrary directions using a setup of multiple loudspeakers. In VBAP, the number of loudspeakers can vary, and they can be positioned in an arbitrary 2-D or 3-D setups. As shown in Fig. 27, VBAP uses the three speakers closest to the desired position of the source to generate the panning gain. For creating the impression of a phantom source between three loudspeakers located at Lijk = [θi, θj, θk], VBAP calculates three weights gijk = [gi, gj, gk]T. Then the weights are calculated from the panning direction θ s by the following equation
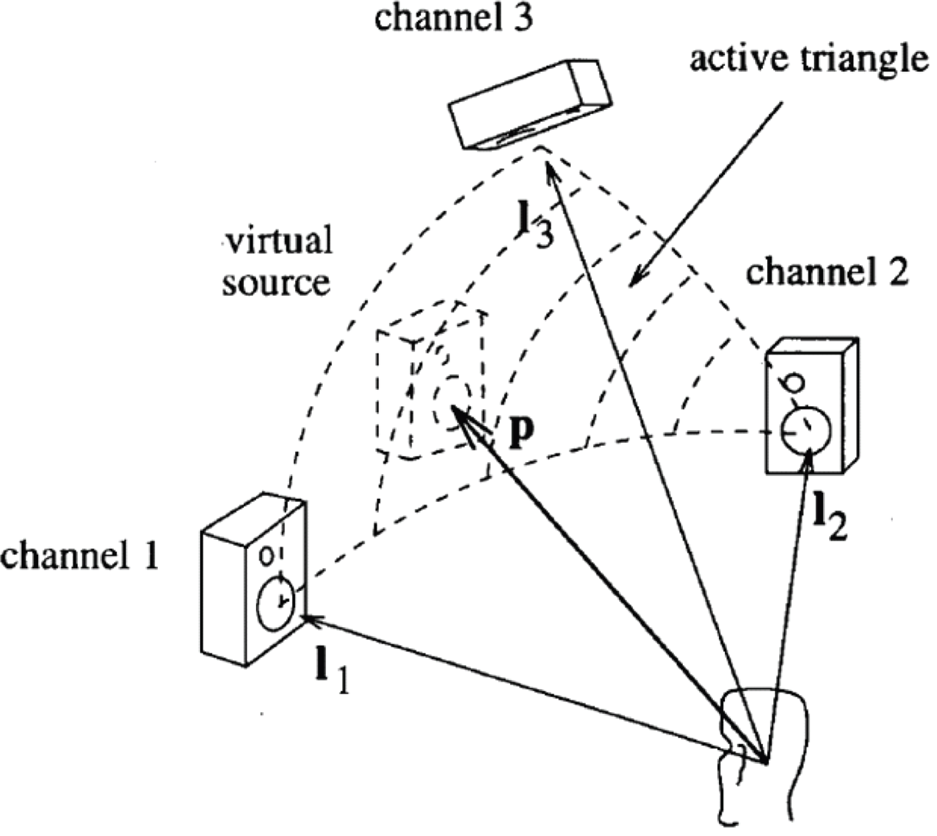
Fig. 27. VBAP panning example, courtesy Pukki [Reference Pulkki22].
In so doing VBAP maximizes sound localization accuracy at the expense of energy spread variability. The energy spread is minimal when the virtual audio source is aligned with a loudspeaker, and is maximal when it is exactly in the middle of a loudspeaker arc or triangle (for configurations with height channels) (Fig. 27).
There have been a few alternative panning methods. For example, VBIP (Vector-Based Intensity Panning) uses intensity panning instead of amplitude panning. DBAP (Distance-Based Amplitude Panning) does not rely on any assumptions regarding speaker array or listener position, which is good for avoiding fixed sweet spots, especially if using irregular loudspeaker layouts. The DBAP technology is based on amplitude panning, applied to a series of speakers. The gain applied to each speaker is calculated according to an attenuation model based on the distance between the sound source and each speaker. Substantial research has also been devoted to irregular loudspeaker layout, which is often encountered in real world. For example, Wang et al. [Reference Wang, Cengarle, Felix Torres and Arteaga28] propose to optimize loudspeaker gains through inverse-matrix, multiplicative-update, or iteratively quadratic programming framework by constraining all gain values of audio sources to be non-negative. The audio object cost function consists of several terms as below:
E cl is a term in favor of representing the audio object at the center of loudness of the audio sources. Edistance is a constraint term for penalizing activating those audio sources that are far from the audio object. Esum-to-one is another constraint term for restricting the sum of the gains to unity with its weight.
B) HOA
The rendering of HOA signals considers how to send the information of different HOA channels to different speakers. Various ambisonic decoders have been proposed in the past, including Sampling Ambisonic Decoder (SAD) [Reference Hollerweger29], Mode-Matching Decoder (MMD) [Reference Hollerweger29, Reference Zotter and Frank30], All-Round Ambisonic Decoding (AllRAD) [Reference Zotter and Frank30], Energy-Preserving Decoder (EPAD) [Reference Zotter, Pomberger and Noisternig31], etc.
In the basic sampling or projection decoding (transpose) method, spherical harmonics are spatially sampled by loudspeakers based on their respective position. For the j th loudspeaker feed pj
where ${D_{SAD}}$![]() is the ambisonic decoding matrix, which is just simply the spherical harmonic function at L loudspeaker positions
is the ambisonic decoding matrix, which is just simply the spherical harmonic function at L loudspeaker positions
is the ambisonic component signal as in equations (4)–(6).
For example, the equation below demonstrates SAD decoding for FOA signal:
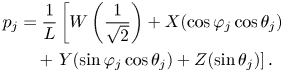
The loudspeaker signals can also be derived through the mode-matching (pseudoinverse) method, which is realized simply by taking the pseudoinverse of the encoding matrix consisting of spherical harmonics $Y_n^m$![]() as shown in equations (4)–(6).
as shown in equations (4)–(6).
Figure 28 plots ambisonic panning function by evaluating the spherical harmonic function in equations (20) and (21) at different directions. Different from VBAP object panning where discrete gains and vectors are used, ambisonic panning employs a continuous virtual panning function of limited angular resolution by assuming a continuous distribution of loudspeakers [Reference Zotter and Frank30]. It can be seen from Fig. 28 that there are non-negligible side-lobes at off-target directions. As a result, when rendering a source signal at a particular direction, the perceived directivity is not as distinct as that with an object audio renderer. The side-lobes can be suppressed by the inclusion of suitable weights in the virtual panning function [Reference Zotter and Frank30]. The so-called Max-rE decoding is to optimize the weights such that the energy concentration toward panning direction is the highest [Reference Zotter, Pomberger and Noisternig31].
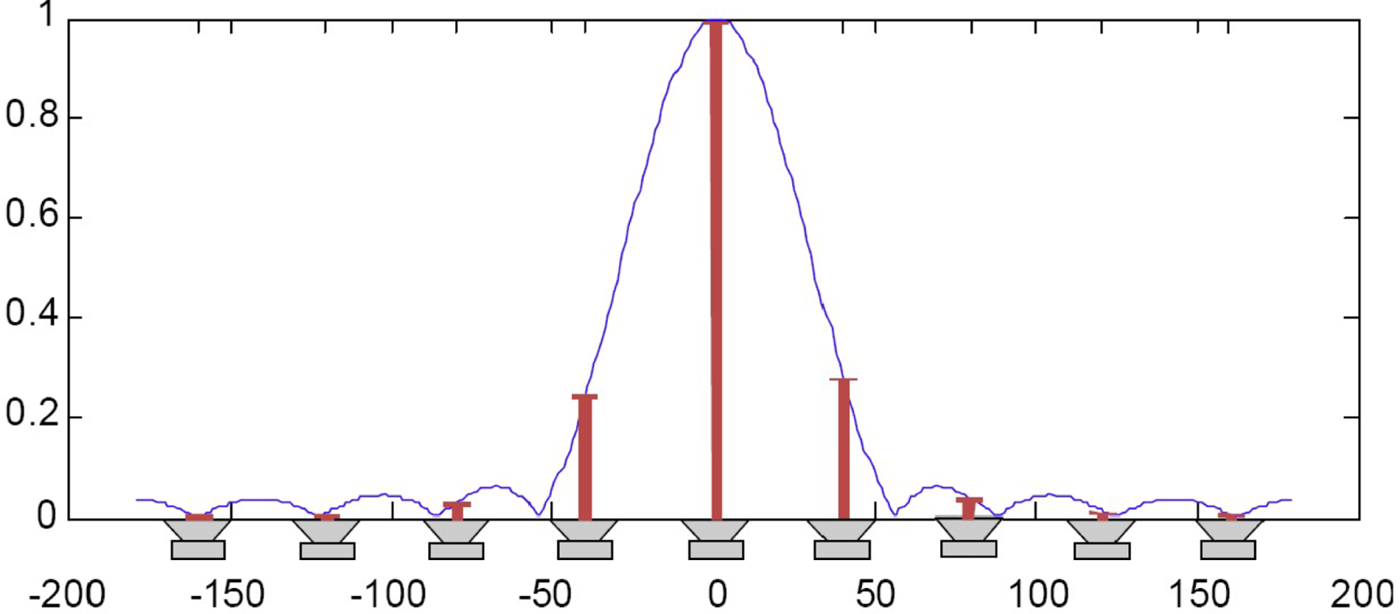
Fig. 28. Ambisonic panning function, courtesy [Reference Hollerweger29].
Ideally the virtual panning function energy is panning-invariant, i.e. the panning function only changes its orientation depending on the panning direction but not its shape. However, this is not applicable in practice where the property is usually lost after the discretization of the virtual panning function by loudspeakers at each particular direction. As a result, the sampling-based ambisonic decoder achieves good results, but breaks down quickly when the loudspeaker arrangement deviates from the ideal layout. Various approaches have been proposed to address the issue of irregular loudspeaker layout [Reference Zotter and Frank30, Reference Benjamin, Heller and Lee32–Reference Ge, Wu and Qu34]. For example, AllRAD is designed to be more robust for non-uniform loudspeaker layout, through a combination of a virtual optimal loudspeaker arrangement and Vector-Base Amplitude Panning. The optimal loudspeaker layout is achieved using a t-design with nodes t ≥2N + 1 [Reference Hardin and Sloane35]. The essence of All-Round Ambisonic Panning (AllRAP) or AllRAD is J virtual loudspeakers of t-design is regarded as J virtual sources and rendered on the L real loudspeakers using VBAP, where J≫L in order to achieve uniform results.
In practice, although imprecise compared with VBAP, ambisonic decoding has constant energy spread regardless of the source direction and loudspeaker layout. This makes ambisonic rendering suitable for certain sound for aesthetic reasons, e.g. ambience or moving audio sources. HOA rendering enjoys growing supports in recent years, with the emergence of several sophisticated HOA decoder plugins supporting up to seventh order, e.g. Sparta [Reference McCormack and Politis13] IEM (https://plugins.iem.at/), freely available to public.
C) Binauralization
Due to the ubiquitous usage of headphones, converting immersive audio to stereo or binaural signals is of critical importance. Binauralization is generally realized through Head Related Transfer Function (HRTF). HRTF describes the sound localization transfer function, including information about a sound traveling from a point to the outer ears of an individual. 3D audio is thus created by multiplying a sound with the HRTFs for that point in the frequency domain. This is equivalent to convolving the input signal with the Head Related Impulse Response (HRIR) in the time domain. Spat revolution from IRCAM has been well used by mixers, content creators in the industry [Reference Carpentier, Noisternig and Warusfel36]. The recent 3D Tune-In project provides a comprehensive review of technical background and various techniques [Reference Cuevas-Rodríguez37], for creating compelling immersive experience, with good externalization yet reasonable complexity.
Numerous studies on binauralization have been conducted from both engineering and perceptual aspect in the scientific field. It is generally agreed that the key factors impacting on the realism and localization accuracy of a virtual source are dynamic cues such as head tracking, environmental cues, e.g. reverberation, individualized HRTFs, and with or without bone-conducted sound. In practice, the first two are commonly looked at for sound source externalization.
Environment cues are often represented by the room transfer function or room impulse response. This function describes the acoustic characteristics between the source and receiver including effects due to reflection at the boundaries, sound absorption, diffraction, and room resonance. Such an impulse response consists of direct, early reflection, and late reverb (Fig. 29).
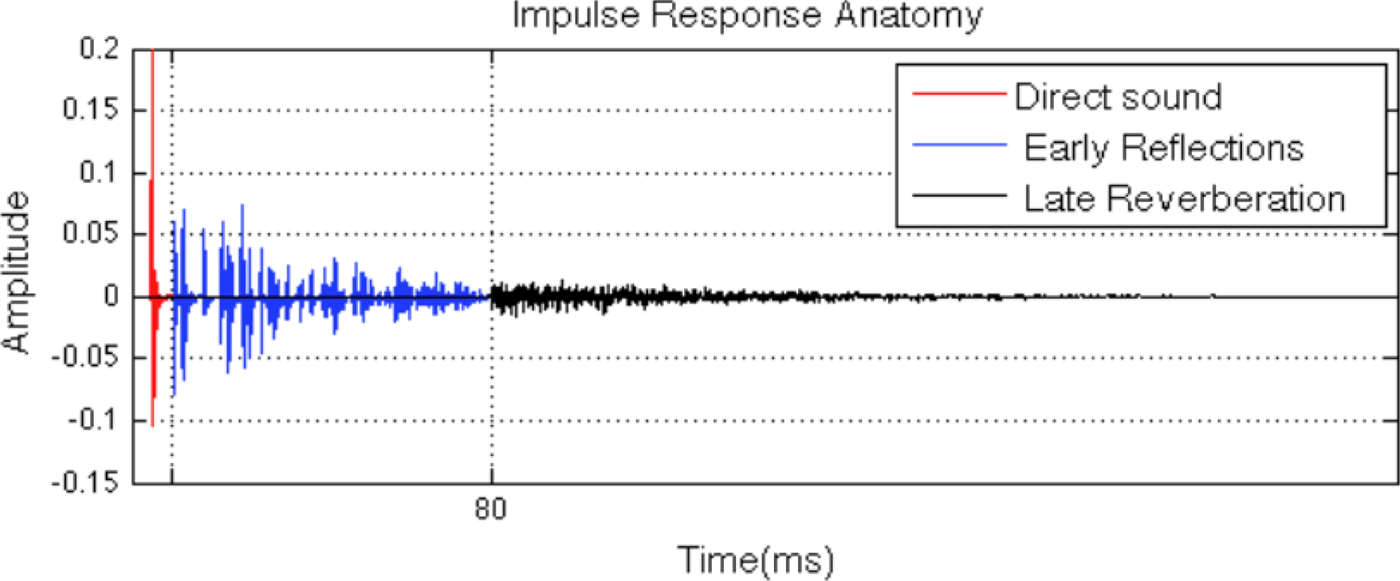
Fig. 29. Impulse response anatomy, courtesy [Reference Georgiou38].
Adding reverb falls into two categories, one being using artificial reverberators based on Feedback Delay Network (FDN) (https://ccrma.stanford.edu/~jos/pasp/FDN_Reverberation.html). Several notable open source implementations exist, for instance Freeverb (https://ccrma.stanford.edu/~jos/pasp/Freeverb.html). The other approach is performing convolutions with real room impulse response, e.g. BRIR. As BRIRs are often long impulse responses, efficient implementation becomes critical. Many work decomposes long impulses into direct or anechoic path and reverb or ambience path, then employing different processing methods for each path. For example, an FOA binauralization approach can be used for the reverb path to make the system scalable [Reference Cuevas-Rodríguez37]. The open-sourced Binaural NGA Renderer (NGA-Binaural) is an addon for the EBU ADM Renderer [Reference Lau and Meier39], where the rendering is divided into three parts: the direct path, the room response, and a non-binaural part. The direct path uses HRTFs as usual, and the room response is represented by the first 60 ms of BRIRs rendered by a smaller number of virtual loudspeakers. Finally, the non-binaural rendering path is realized by an adjusted stereo rendering to maintain correct object positioning on headphones.
One aspect of the binauralization is near-field compensation for HRTF. It has been found that as the sound source approach the head the ILD increases: the level at the ipsilateral ear increases while the level at the contralateral ear decreases. Low frequencies are boosted more than high frequencies on the ipsilateral side while high frequencies are attenuated more than the low frequencies on the contralateral side. These two effects give rise to increased bass response for sound sources close to the head. [Reference Romblom and Cook40] proposes to use difference filters based on a spherical head model and a geometrically accurate HRTF lookup scheme to compensate near-field effect without actual HRTF measurements.
FOA binauralization is of particular interests because FOA has become the most widely adopted 360 audio format in VR/AR due to its good tradeoff between quality and efficiency. VR platforms such as YouTube supports FOA as the foundational format to allow rendering both object audio and captured soundfield. There are several studies specifically on FOA binauralization, mainly based on direct-ambience decomposition, where sharper localization and good externalization can be achieved, e.g [Reference Politis, Tervo and Pulkki41–Reference Schörkhuber and Höldrich43]. However, these signal-dependent techniques suffer similar stability problems as in other applications. That is, when the analysis goes wrong, the results can be worse than the output of conventional methods, leading to unpleasant rendering experience.
Using head tracking to improve binaural experience has a long history [Reference Noisternig, Sontacchi, Musil and Holdrich44]. Popularized by the VR/AR devices, the once expensive and bulky motion tracking devices become affordable and compact. The core of such devices is an IMU (Inertial Measurement Unit) sensor, which is a complete package that includes an accelerometer, a gyroscope, and a magnetometer sensor. An accelerometer sensor is used to sense both static and dynamic acceleration of an object, and a gyroscope sensor measures the angular momentum around the three axes of rotation: x, y, and z (roll, pitch, and yaw). The magnetometer sensor senses the earth's magnetic field to get a compass heading to correct the gyroscope sensor. The position values are then estimated through sensor-fusion algorithms, which are fed to the binaural renderer in real time [Reference Romanov, Berghold, Frank, Rudrich, Zaunschirm and Zotter45]. Dynamic binaural synthesis is then realized via HRTF interpolation or efficient ambisonic soundfield rotation.
In practice “generic” HRTFs are often used for binauralization. However, HRTFs vary from person to person. A mismatch between the listener's HRTF and the one that is used to encode the 3D audio signal can lead to “internalized” sound image and inaccurate localization. Unfortunately, it is quite difficult to obtain a personalized HRTF measurement. Some techniques attempted include taking photos [Reference Meshram, Mehra, Yang, Dunn, Frahm and Manocha46] or simply asking users to provide some rough estimation of size of their head and torso as well as the form of ears. Then HRTFs are approximated by using analytical solutions, such as a “snowman” model. Nevertheless, such a simplified model can only generate HRTFs matching measured HRTFs at low frequencies, missing detailed spectral features at high frequencies especially due to pinnae. Another approach is to correlate anthropometric measurements with those of a database of measured HRTFs. [Reference Meshram, Mehra, Yang, Dunn, Frahm and Manocha46] proposes a more sophisticated method where consumer-grade cameras are used to generate a 3D mesh followed by a numeric sound simulation technique. Alternatively, or additionally HRTFs can be customized by letting users listen to 3D audio sound and tuning iteratively. In [Reference Islam and Tashev47], a multi-modal algorithm is used to estimate anthropometric features which aggregate signals of both microphone and IMU. The algorithm exploits the basic principles of sound propagation around the head, magnetic field intensity attenuation with the distance, and acceleration caused by the human head movement, to extract features that are representative of human head dimensions.
D) Virtual surround
Virtual surround closely relates to binauralization, with a key extension of cross-talk cancellation (XTC). There are many use cases where only two loudspeakers can be used for playback immersive audio content. This can be due to economic reasons, or the limitation of form factors. Some typical scenarios include mobile phones, soundbars, laptops, desktop PC speakers, TV, etc. It is often desirable to generate immersive audio experience using the fewest number of speakers.
When listening through loudspeakers at binaural signals either recorded directly or convolved with Binaural Impulse Responses (BIRs), the signal emitted from the left loudspeaker reaches also the right ear, and vice-versa. Therefore, cross-talk cancelling filters must be applied in order to present the original binaural signal to the listeners [Reference Nufire48] (http://pcfarina.eng.unipr.it/Aurora/crostalk.htm) (Fig. 30).
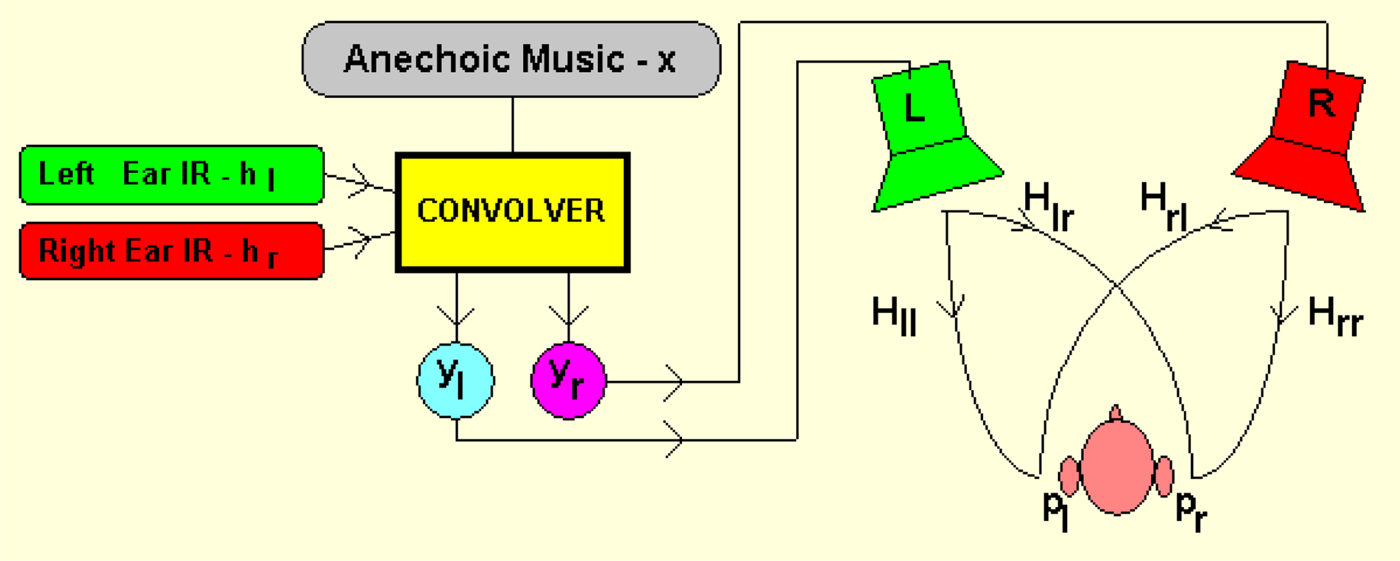
Fig. 30. A schematic representation of binaural signals rendering through two loudspeakers courtesy (http://pcfarina.eng.unipr.it/Aurora/crostalk.htm).
Conventional system employs inverting transfer functions from the loudspeakers to ears (often HRTF filters), and applying such filters to the original BIRs prior to the convolution with the anechoic signals, or directly to the binaural signals. The filters are further factorized into equalization filter (E) and cross talk cancellation filter (C) as shown in the figure below and the following formulations (Fig. 31).
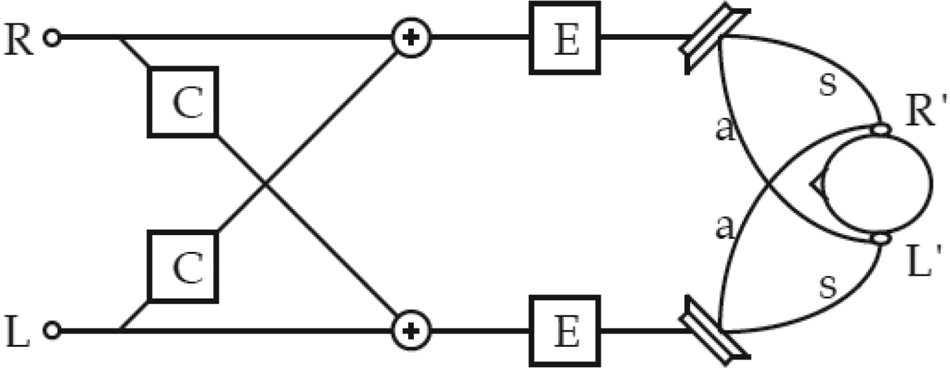
Fig. 31. Building blocks of an XTC system, courtesy [Reference Nufire48].
A simplified formulation of HRTF-based XTC approach is as below [Reference Anushiravani49]
where Out is the signal received at the ear and In is the input to the loudspeakers, and HRTF represents contralateral and ipsilateral transfer functions. The perfect HRTF-based XTC can then be derived as:
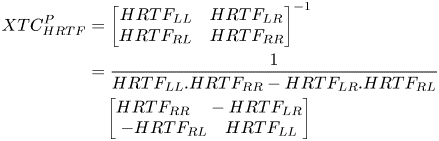
The matrix inversion process can introduce instability, which leads to spectral coloration thus reduced output quality. In order to overcome this problem, regularization is frequently used to reduce the effect of the ill-conditioned frequencies at the cost of losing some amount of XTC accuracy [Reference Anushiravani49].
Choueriri [Reference Choueiri50] points out that an XTC level of over 20 dB is required for accurate transmission of ITD and ILD cues. This is rather difficult to achieve in practice due to reverberation, HRTF mismatch, and movement. In order to circumvent the problems associated with the conventional HRTF methods, he then proposes a BACCH filter that uses a free field two-point source model to achieve more robust performance against spectral coloration, head movement, and less individual-dependent. Evaluation [Reference Anushiravani49] demonstrates the effectiveness of BACCH and regularization on coloration reduction and improved overall quality.
To address the issue of restricted sweet spot during head movement, researchers from Microsoft [Reference Song, Zhang and Florencio51] proposed to use camera to track head movement and was able to create variable sweet spots based on head tracking.
E) Upmix
When multi-channel playback is available, generating immersive audio from fewer channels automatically, e.g. from stereo signals, is a highly desired feature in many real-world applications. There has been extensive research on upmixing stereo material to 5.1 format ever since the early days of 5.1 surround sound era [Reference Faller52–Reference Lee54]. With the advent of object audio, HOA, the need to upmixing existing 5.1/7.1 CBA or low-order ambisonics, e.g. FOA, to new immersive audio formats has been called out for improved experience, taking advantage of the new playback installation.
Unfortunately, blind upmixing without any assistance of side information (metadata) proves to be extremely challenging. As a means to improve the spatial immersive experience, algorithms have been proposed to upmix the audio signals to height (overhead) speakers, such as from surround 5.1 to surround 7.1.2, where the “.2” refers to the number of height speakers [Reference Wang, Lu, Chen and Hu55], or more generally to upmix traditional CBA to full 3D object audio system with height. The basic approach is similar to other signal-dependent upmixing methods, in that the audio signal is first decomposed into a diffuse signal and a direct signal. Then an audio bed signal, including height channel, is generated based on the diffuse signal. An audio object is extracted from the direct signal, and the estimated metadata include height information of the audio object. During rendering, the audio bed is rendered to a predefined position and the audio object is rendered according to the metadata.
Professional DAW begins to add ambisonic support by providing upmixing from stereo and surround to HOA, e.g. third-order ambisonics (https://www.pro-tools-expert.com/home-page/2020/1/25/upmixing-to-ambisonics-nugen-halo-upmix-and-perfectsurround-penteo-16-pro-tested).
Machine learning-based source separation has been attempted for extracting particular audio stems, which could find applications in upmix systems. For instance, non-negative matrix factorization is frequently used in music source separation in the Music Information Retrieval (MIR) research community. The fast development of deep learning has given a huge boost to source separation research, making automatic audio object extraction and upmixing one step closer to reality. A notable recent example is the Spleeter system, a state-of-the-art music source separation system open sourced by Deezer [Reference Hennequin, Khlif, Voituret and Moussallam56] where music audio files can be separated into two stems (vocals and accompaniments), four stems (vocals, drums, bass, and other) or five stems (vocals, drums, bass, piano, and other). The models are trained using a U-net architecture, which is an encoder/decoder Convolutional Neural Network (CNN) with skip connections. With 12 layers (6 layers for the encoder and 6 for the decoder), the model can separate mix audio files into 4 stems 100 times faster than real-time on a single Graphics Processing Unit (GPU). Facebook also releases a U-net based music source separation tool called Demucs [Reference Défossez, Usunier, Bottou and Bach57], achieving highly competitive results. Other well-known systems include Open-Unmix, based on a three-layer bidirectional Long Short-Term Memory (LSTM) (https://github.com/sigsep/open-unmix-pytorch). Although the output of these systems is still far from perfect, the quality has improved tremendously compared to old systems, representing a viable option for commercial applications.
V. INDUSTRY TREND
A) Broadcast, film
Broadcast and film industry is arguably the central arena for immersive content creation and distribution. ATSC (Advanced Television Systems Committee) 3.0 is the latest standard for television broadcasting covering primarily the USA while the counterpart in Europe is DVB-T (Digital Video Broadcasting – Terrestrial). ATSC 3.0 has included both Dolby AC-4 and MPEG-H 3D audio, so is DVB Ultra HD specification. DVB ETSI TS 101 154 [58] defines Next Generation Audio (NGA) that includes immersive audio with height elements, personalized audio for end users, and Audio Objects. Based on the Audio Definition Model (ADM) [59], EBU released an open source NGA renderer (EAR) [60]. The ADM Renderer (EAR) is at the heart of the new ITU ADM Renderer specification for NGA [61] where the original EAR was extended with features from Dolby and Fraunhofer IIS.
In cinema, the development in SMPTE 2098 suite is hailed as a game-changer for the audio industry because the immersive audio for cinema has finally reached the interoperability stage. As long as the rendering system is compliant with the SMPTE standards, theaters are able to play the same Digital Cinema Packages (DCP) into their own proprietary systems. It is expected that new immersive audio formats would steadily replace currently prevailing 5.1 surround sound around the world.
B) Music
Music is predominantly stereo. Multichannel music, e.g. 5.1, has not entered the mainstream even as of today. Nevertheless, the call for more immersive and interactive music has become stronger. Companies such as Dolby and Sony are at forefront of pushing the adoption of object audio in music production. The idea is to allow the user to hear vocal and instruments as objects in a spherical 3D space.
360 Reality Audio (https://www.sony.com/electronics/360-reality-audio), initiated by Sony, is first launched in fall 2019, with music streaming services from Amazon Music HD, Deezer, nugs.net and TIDAL. The underlying technology is MPEG-H Audio (https://www.iis.fraunhofer.de/en/ff/amm/broadcast-streaming/mpegh.html). The newly released Amazon Echo Studio premium smart speaker began support of 360 Reality Audio. Sony's 360 Reality Audio received a boost from semiconductor industry with MediaTeck's announcement of support in its audio chipsets ().
Dolby Atmos Music (https://www.dolby.com/experience/music/), as the name implied, is Dolby Atmos for music. Streaming Dolby Atmos Music is supported on TIDAL and Amazon Music HD. Thanks to the early start of Dolby Atmos in films and home cinema, there appears to be more compatible hardware available for playing back Dolby Atmos Music, ranging from smartphones, soundbars, and TVs.
One of the challenges for promoting immersive audio in music is the lack of object audio-based content. It is reported that there are more than 2000 songs in immersive audio format from big Labels such as Sony Music, Universal Music and Warner Music as well as live concerts offered by Live Nation (https://www.iis.fraunhofer.de/en/ff/amm/broadcast-streaming/mpegh.html). Compared with stereo content, this number can hardly be anything significant. How to amass more immersive audio content in a timely manner is without doubt a big hurdle faced by the music industry. The good news is, with the improvement of deep learning-based audio source separation systems, it becomes possible to extract multiple tracks (audio objects) automatically with minimum audible artifacts.
C) Automotive
Audio has always played a crucial role in the automotive industry. With the rise of electric car and self-driving technologies, immersive audio is increasingly believed to be a vital part of modern in-vehicle entertainment experience. This is manifested by last year's AES automotive conference, featuring by keynote speech such as “Immersive Audio Listening Experience in Cars – the Future of Music”, as well as prototypes for immersive music playback in a car demonstrated by Fraunhofer, Audi and Sony.
Fraunhofer's Sonamic Panorama () solution essentially employs a direct-ambience decomposition based upmix algorithm to convert stereo content into surround format. Further optimization is performed for every vehicle type through applying parameters with the separate Sonamic Panorama Tuning Library (Fig. 32).
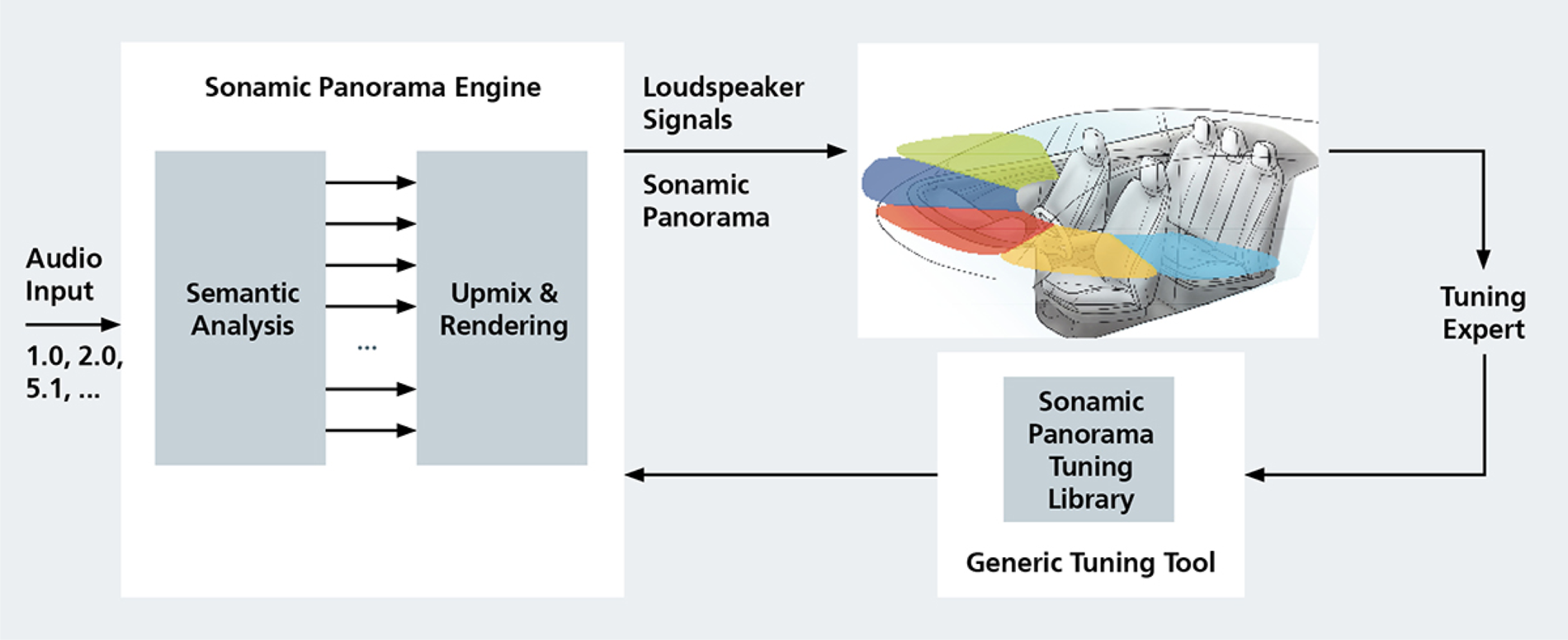
Fig. 32. Fraunhofer's Sonamic Panorama, courtesy (https://audioxpress.com/article/automotive-audio-solutions-redefining-surround-sound-in-cars/).
Harman's Virtue Venues [Reference von Türckheim, von dem Knesebeck and Münch62] system simulates the acoustics of existing concert halls with artificial reverberation. Through using in-car microphones and de-reverberation, the system aims at creating a consistent spatial impression even in the presence of masking driving noise.
Sennheiser introduces AMBEO Mobility Audio (https://en-ae.sennheiser.com/ambeo-mobility) as an immersive audio solution for in-car entertainment and communication. The solution consists of high-fidelity speakers, headrest sound design for personalization, microphone arrays for voice calls. The system can reportedly handle specific 3D audio sources and turn stereo material into multichannel audio through its AMBEO upmix algorithm. Sennheiser also partnered with Continental to present a speakerless audio system for the vehicle interior which combines AMBEO 3D audio technology with Continental's Ac2ated Sound system.
As the automotive industry observing three powerful trends: electrification, automation and connectivity, customer expectations and driving manufacturers increasingly turn to software to address them. This progressing to “software-defined vehicles” would naturally lead more opportunities to real-time immersive audio processing and rendering.
D) VR/AR/XR
Without doubt VR/AR contributes substantially to the adoption of immersive audio, especially for the resurgence of ambisonic. Google acquired Trinity audio and then open sourced Resonance audio (https://resonance-audio.github.io/resonance-audio/) [Reference Gorzel63]. Facebook acquired Two Big Ears and released Facebook360 Workstation, which has been in active maintenance up to today (https://facebook360.fb.com/spatial-workstation/). Partly due to the support from Google and Facebook, ambisonic has become the de facto standard VR audio format in the industry, even though a large percentage of 360 videos on the Internet are still in stereo format. In the gaming industry where VR experiences flourishing demand, it is generally recognized that object audio can be complemented by ambisonic for representing ambience or as an efficient renderer option. Main game engines or middlewares such as Unreal, Unity, Wwise, and Fmod all have good support of both object audio and ambisonics nowadays. In augmented/mixed reality headsets (AR/MR), Microsoft Research has put enormous effort on delivering compelling immersive audio on its signature Hololens [Reference Tashev64]. As these devices are predominantly battery powered, the hardware's computing power is the limiting factor of delivering sophisticated audio systems. Recognizing the need for audio-centered computation, Qualcomm's latest Snapdragon XR2 5 G platform (https://www.qualcomm.com/products/snapdragon-xr2-5g-platform) is reported to support rich 3D audio features, paving the way to more realistic immersive audio experience in the next generation XR devices.
E) Home theater, consumer electronics
It is no doubt that for immersive audio to reach mass market, home and consumer electronics platforms are needed. All the new immersive audio formats have a thinner version tailored to home environment, from traditional A/V receivers and OTT (over-the-top) devices. Dolby Atmos for home recommends a 7.1.2 setup with upward-firing speakers, and supports up to 128 audio objects and 34 loudspeakers (https://professional.dolby.com/tv/home/dolby-atmos/). Major soundbar brands start to support Dolby Atmos and DTS:X, including Sony, Sonos, LG, Samsung, etc. Audio chipset makers such as NXP and MediaTek begin support of Dolby Atmos and DTS:X (https://www.nxp.com/company/blog/nxp-brings-dolby-atmos-and-dtsx-to-living-rooms-everywhere-with-immersiv3d-audio-solution:BL-BRINGS-DOLBY-ATMOS-AUDIO-SOLUTION).
Delivering immersive audio experience through headphones has always attracted a lot of interests due to its wide access to mass user base. For example, Ossic × headphone, once a starred Kickstarter project, generated significant interests by claiming the support of headtracking, personalized HRTF and multiple individual speaker drivers. Coincide with the rise of VR/AR, Ossic × won rave reviews, and appeared to fulfill some key quests of many audiophiles. Unfortunately the headphone was not delivered and the company was shut down eventually (https://www.kickstarter.com/projects/248983394/ossic-x-the-first-3d-audio-headphones-calibrated-t). Startup project Vinci headphone is yet another bold attempt of embracing more advanced features into headphones including immersive audio (https://www.amazon.com/VINCI-Smart-Headphones-Artificial-Intelligence/dp/B072ML2CT4). It supports binaural sound recording with two microphones, interactive binaural rendering via integrated head tracking sensors (http://yun-en.twirlingvr.com/home/index/2017-02-27). Dolby Dimension Bluetooth headphones (https://www.pcmag.com/reviews/dolby-dimension) also feature head-tracking 3D audio on top of other standard features such as active noise cancellation. Rather than building head-tracking capable headphones, companies and audio engineers develop head-tracking accessories as headphone companions for immersive audio. For example, Waves' nx headtracker (https://www.waves.com/nx) has found some applications in professional audio communities and headphones (https://www.pcmag.com/reviews/audeze-mobius).
The explosive growth of True Wireless Stereo (TWS) earphones provides exciting new opportunities for immersive audio. Particularly, the recent support of spatial audio in Apple Airpods Pro represents a crucial milestone in bringing immersive audio to mass market. Similar to VR/AR devices, Apple's solution uses the gyroscope and accelerometer in the AirPods Pro to track the head motion and render binaural content accordingly. It's likely the actual binaural rendering occurs on the iPhone, iPad, or other Apple devices, and the AirPods Pro is merely sending the gesture data and receiving binaural signal streams via Bluetooth. Nonetheless, with engineering optimization it's possible to perform all the audio upmix and virtualization on the earphones, avoiding all the potential latency and packet loss issues caused by the Bluetooth link. The downside is this could cause more power drain on the TWS earphones where battery life is one of the essential user concerns.
Immersive audio also finds applications in many other areas, for example, in audio conferencing. Early immersive telepresence systems from Cisco and Polycom emphasize high-fidelity audio and video, with fairly simple treatment on the spatial audio aspect. Dolby Voice is likely the first end-to-end large-scale commercial audio conferencing system in utilizing ambisonic from capture, transmission to rendering (https://www.dolby.com/us/en/brands/dolby-voice.html). With faster connectivity (e.g. 5G) and more versatile communication devices such as XR headsets and TWS, it is not unreasonable to expect immersive audio conferencing would be set for explosive growth in the foreseeable future.
VI. CONCLUSION
This review provides merely a glimpse of the current development of immersive audio. With key market participants made significant advances in rolling out new codecs to the consumer mass market, industry experts are predicting a big explosion of immersive audio in the next 2–4 years. Nevertheless, hurdles remain in mass content production and distribution as the content producers would naturally be faced with a learning curve in mastering the new technology.
ACKNOWLEDGEMENT
The author wishes to thank the Twirling team for their support in completing the manuscript.
CONFLICT OF INTEREST
The author is the founder and CEO of Twirling Technologies, maker of Twirling720 soundfield microphones.
Xuejing Sun received a bachelor degree from Peking University and received his Ph.D. degree from Northwestern University in 2002. He is now the CEO of Twirling Technologies, a company specializing in audio capture and rendering, as well as developing audio AI on edge devices.



































