Published online by Cambridge University Press: 29 August 2014
When the distribution of the number of claims in an interval of time of length t is mixed Poisson and the moments of the independent distribution of individual claim amounts are known, the moments of the distribution of aggregate claims through epoch t can be calculated (O. Lundberg, 1940, ch. VI). Several approximations to the corresponding distribution function, F(·, t), are available (see, e.g., Seal, 1969, ch. 2) and, in particular, a simple gamma (Pearson Type III) based on the first three moments has proved definitely superior to the widely accepted “Normal Power” approximation (Seal, 1976). Briefly,
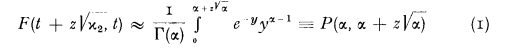
where the P-notation for the incomplete gamma ratio is now standard and α, a function of t, is to be found from
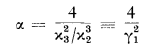
the kappas being the cumulants of F(·, t). An excellent table of the incomplete gamma ratio is that of Khamis (1965).
The problem that is solved in this paper is the production of an approximation to U(w, t), the probability of non-ruin in an interval of time of length t, by using the above mentioned gamma approximation to F(·, t).