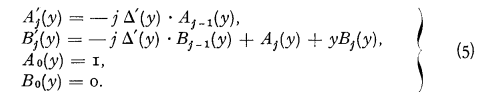Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Santomero, Anthony M.
and
Vinso, Joseph D.
1977.
Estimating the probability of failure for commercial banks and the banking system.
Journal of Banking & Finance,
Vol. 1,
Issue. 2,
p.
185.
Mack, Thomas
1984.
Premium Calculation for Deductible Policies with an Aggregate Limit.
ASTIN Bulletin,
Vol. 14,
Issue. 2,
p.
105.
Seri, Raffaello
and
Choirat, Christine
2015.
COMPARISON OF APPROXIMATIONS FOR COMPOUND POISSON PROCESSES.
ASTIN Bulletin,
Vol. 45,
Issue. 3,
p.
601.

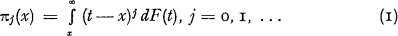
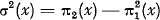 the variance thereof.
the variance thereof.