Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kremer, Erhard
1982.
Rating of Largest Claims and Ecomor Reinsurance Treaties for Large Portfolios.
ASTIN Bulletin,
Vol. 13,
Issue. 1,
p.
47.
Kremer, Erhard
1983.
Distribution-free upper bounds on the premiums of the LCR and ECOMOR treaties.
Insurance: Mathematics and Economics,
Vol. 2,
Issue. 3,
p.
209.
Kremer, Erhard
1984.
Premium Calculation in Insurance.
p.
285.
Teugels, Jozef L.
1984.
Statistical Extremes and Applications.
p.
253.
Kremer, E.
1984.
An asymptotic formula for the net premium of some reinsurance treaties.
Scandinavian Actuarial Journal,
Vol. 1984,
Issue. 1,
p.
11.
Kremer, Erhard
1985.
Finite formulae for the premium of the general reinsurance treaty based on ordered claims.
Insurance: Mathematics and Economics,
Vol. 4,
Issue. 4,
p.
233.
Kremer, Erhard
1986.
DGOR.
p.
218.
Kremer, Erhard
1986.
Simple formulas for the premiums of the LCR and ECOMOR treaties under exponential claims sizes.
Blätter der DGVFM,
Vol. 17,
Issue. 3,
p.
237.
Kremer, Erhard
1988.
A General Bound for the Net Premium of the Largest Claims Reinsurance Covers.
ASTIN Bulletin,
Vol. 18,
Issue. 1,
p.
69.
Kremer, Erhard
1988.
Eine verallgemeinerte statistische LCR-Tarifierungsmethode.
Blätter der DGVFM,
Vol. 18,
Issue. 4,
p.
291.
Rytgaard, Mette
1990.
Estimation in the Pareto Distribution.
ASTIN Bulletin,
Vol. 20,
Issue. 2,
p.
201.
Wüthrich, Mario V.
2004.
Extreme Value Theory and Archimedean Copulas.
Scandinavian Actuarial Journal,
Vol. 2004,
Issue. 3,
p.
211.
Beirlant, Jan
2004.
Encyclopedia of Actuarial Science.
Ladoucette, Sophie A.
and
Teugels, Jef L.
2006.
Reinsurance of large claims.
Journal of Computational and Applied Mathematics,
Vol. 186,
Issue. 1,
p.
163.
Klemmt, Heinz-Jürgen
2008.
Monotonie des Hill-Schätzers in endlichen Stichproben.
Blätter der DGVFM,
Vol. 29,
Issue. 2,
p.
245.
Beirlant, Jan
2014.
Wiley StatsRef: Statistics Reference Online.
2017.
Reinsurance.
p.
309.
Fan, Yuguang
Griffin, Philip
Maller, Ross
Szimayer, Alexander
and
Wang, Tiandong
2017.
The Effects of Largest Claim and Excess of Loss Reinsurance on a Company’s Ruin Time and Valuation.
Risks,
Vol. 5,
Issue. 1,
p.
3.
Czapiewski, Colin
Dahl, Patrik
Havning, Mette
and
Mack, Thomas
2018.
GUNNAR BENKTANDER 1919–2018.
ASTIN Bulletin,
Vol. 48,
Issue. 3,
p.
961.
Zhang, Yiying
2021.
On transform orders for largest claim amounts.
Journal of Applied Probability,
Vol. 58,
Issue. 4,
p.
1064.
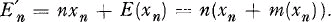 Intuitively we feel that
Intuitively we feel that 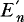 is a good approximation for En.
is a good approximation for En.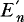 is a good approximation for En, being slightly on the safe side. We further include a proof given by G. Ottaviani that the inequality
is a good approximation for En, being slightly on the safe side. We further include a proof given by G. Ottaviani that the inequality 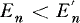 always holds.
always holds.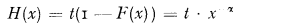
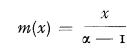 .
.