Article contents
Note on the Background to the Subject: Theory of Risk, Fundamental Mathematics and Applications
Published online by Cambridge University Press: 29 August 2014
Extract
By a general theorem the necessary and sufficient condition for a function φ0 (σ) being completely monotonic for σ lying in the right semi-plane, i.e. that the nth derivative with respect to σ has the sign of (— 1)n, is that the function may be represented by the Laplace-Stieltjes integral 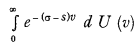 , where U (v) is a non-decreasing function of v, independent of σ and bounded in every finite interval, σ a real or complex variable represented in the right semi-plane, s a real constant ≤ the real part of σ. By the notation φn (σ) we designate
, where U (v) is a non-decreasing function of v, independent of σ and bounded in every finite interval, σ a real or complex variable represented in the right semi-plane, s a real constant ≤ the real part of σ. By the notation φn (σ) we designate 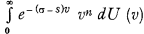 , which for U (v) being independent of σ, as assumed above, is equal to
, which for U (v) being independent of σ, as assumed above, is equal to 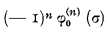 .
.
Definition 1. A compound Poisson process (in the narrow sense) is a process for which the probability distribution of the number of changes in the random function Y (t), constituting the process, occurring while the parameter, which is represented on the positive real axis, is in the interval (o, t) for every value of t, is defined by the following relation
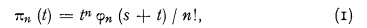
the function φn (σ) being defined by the integral given above and subject to the condition that φ0 (σ) tends to unity, when σ tends to s. The function U (v) in the integrand of φn (σ) is, then, a distribution function which defines the risk distribution, in this case said to be t-independent.
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1961
References
Literature Cited
- 2
- Cited by


