Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T12:40:41.975Z Has data issue: false hasContentIssue false
  • English
  • Français

On an Integral Equation for Discounted Compound – Annuity Distributions

Published online by Cambridge University Press:  07 February 2018

Colin M. Ramsay
Colin M. Ramsay*
Affiliation:
Actuarial Science, University of Nebraska, Lincoln NE, USA68588-0307, (402) 472-5823.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a risk generating claims for a period of N consecutive years (after which it expires), N being an integer valued random variable. Let Xk denote the total claims generated in the kth year, k ≥ 1. The Xk's are assumed to be independent and identically distributed random variables, and are paid at the end of the year. The aggregate discounted claims generated by the risk until it expires is defined as 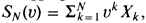where υ is the discount factor. An integral equation similar to that given by Panjer (1981) is developed for the pdf of SN(υ). This is accomplished by assuming that N belongs to a new class of discrete distributions called annuity distributions. The probabilities in annuity distributions satisfy the following recursion:

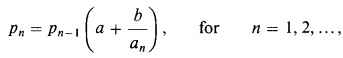
where an is the present value of an n-year immediate annuity.

Keywords

Annuity distributionsintegral equationaggregate discounted claims
Type
Articles
Information
ASTIN Bulletin: The Journal of the IAA , Volume 19 , Issue 2 , November 1989 , pp. 191 - 198
Copyright
Copyright © International Actuarial Association 1989

References

Boogaerts, P. and Crijns, V. (1987) Upper bounds on ruin probabilities in case of negative loadings and positive interest rates. Insurance: Mathematics and Economics 6, 221–232.Google Scholar
Boooaert, P., Haezendonck, J. and Delbaen, F. (1988). Limit theorems for the present value of the surplus of an insurance portfolio. Insurance: Mathematics and Economics 7, 131–138.Google Scholar
Garrido, J. (1988) Diffusion premiums for claim severities subject to inflation. Insurance: Mathematics and Economics 7, 123–129.Google Scholar
Gerber, H. (1971) The discounted central limit theorem and its Berry-Esseen analogue. Annals of Mathematical Statistics, Vol. 42, 1, 389–392.Google Scholar
Malik, S. (1984) Introduction to convergence. Halstead Press, New York.Google Scholar
Panjer, H. (1981) Recursive evaluation of a family of compound distributions. ASTIN-Bulletin 12, 22–26.CrossRefGoogle Scholar
Ströter, B. (1985) The numerical evaluation of the aggregate claim density function via integral equations. Blätter der Deutschen Gesellschaft für Versicherungsmathematik 17, 1–14.Google Scholar
Sundt, B. and Jewell, W. (1981) Further results on recursive evaluation of compound distributions. ASTIN Bulletin 12, 27–39.Google Scholar
Waters, H. (1983) Probability of ruin for a risk process with claim cost inflation. Scandinavian Actuarial Journal 66, 148–164.CrossRefGoogle Scholar
Willmot, G. (1988) Sundt and Jewell's family of discrete distributions. ASTIN Bulletin 18, 17–29.Google Scholar