No CrossRef data available.
Published online by Cambridge University Press: 29 August 2014
In this paper we are going to study some properties of a stochastic process, which has been proposed by Cramér (1968) as a model of the claims arising in an insurance company. This process has been studied by Cox in a different context. A few elementary results, concerning moments, are given by Cox and Lewis (1966). The present paper will be a survey of some results derived by the author (1970:1) and (1970:2). For detailed proofs we refer to these papers.
Let λ(t) be a real-valued stochastic process, such that P{λ(t) < o} = o. We further assume that Eλ(t) = 1 and that Eλ2(t) < ∞ for every fixed value of t. We denote the covariance
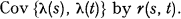
The process λ(t) will play the role of an intensity function. That means, that for every fixed realization of the process, the probability of
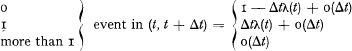
and that the number of events in disjoint intervals are independent.
We now define a point process N(t), where N(t) is the number of events which have occurred in (o, t]). With this definition we get
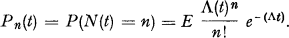
where
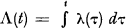
The integral is assumed to exist almost surely. This process will be called the N-process.