Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T13:54:38.452Z Has data issue: false hasContentIssue false
  • English
  • Français

The propensity to cause accidents*

Published online by Cambridge University Press:  29 August 2014

Christoph Haehling von Lanzenauer  and
William N. Lundberg
Christoph Haehling von Lanzenauer
Affiliation:
Canada
William N. Lundberg
Affiliation:
Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Information relating to the expected number of losses is of importance in automobile insurance systems. The distribution of risks by number of losses per year may be based on the following model

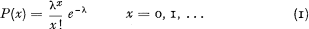
with λ representing the average number of losses per year. This distribution is the Poisson distribution. Tests of this model versus actual observations often indicate significant deviation. This discrepency can result from the constancy of λ which makes the model appropriate for an individual but would require an isohazardous population when applied to a group of individuals. In reality, however, λ will vary from individual to individual. A model accounting for this spread in λ is given in

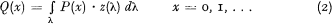
where z(λ) is a distribution describing the spread of λ. The results of model (2) certainly will depend on the form of z(λ). It has been hypothesized that z(λ) can be represented by (3)

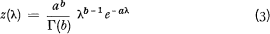
which is a Pearson Type III [1, 5, 7]. With this assumption model (2) becomes the negative binominal distribution 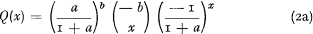with a mean of 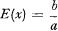and a variance of

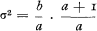
If the observed mean is 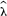and the observed variance 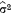it is possible to determine a and b by solving the above equations for mean and variance. Thus 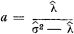and

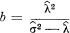
The results indicate an improved fit to actual observations [1, 5, 6].

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 7 , Issue 2 , September 1973 , pp. 154 - 164
Copyright
Copyright © International Actuarial Association 1974

Footnotes

*

This research was supported by a grant from the Associates' Workshop in Business Research 1971, School of Business Administration, University of Western Ontario.

References

[1]Dropkin, L., Some Considerations on Automobile Rating Systems Utilizing Individual Driving Records, PCAS, Vol. 46, 1959.Google Scholar
[2] Gesamtstatistik der Kraftfahrtversicherung, 1967.Google Scholar
[3]Haehling von Lanzenauer, C., Entscheidungsregeln für das optimale Verhalten in der Kraftfahrzeugversicherung, Unternehmensforschung, Vol. 13, No. 3, 1969.Google Scholar
[4]Haehling von Lanzenauer, C., Optimal Claim Decisions in Automobile Insurance Systems with Merit Rating Structures, University of Western Ontario, School of Business Administration, Working Paper No. 51.Google Scholar
[5]Harwayne, F., Merit Rating in Private Passenger Automobile Liability Insurance and the California Driver Record Study, PCAS, Vol. 46, 1959.Google Scholar
[6]Hewitt, C., The Negative Binominal Applied to the Canadian Merit Rating Plan for Individual Automobile Risks, PCAS, Vol. 47, 1960.Google Scholar
[7]Mehring, J., Strukturprobleme in der Kraftfahrt-Haftpflichtversicherung, Blatter der Deutschen Gesellschaft für Versicherungsmathematik, Vol. 5, No. 1, 1960.Google Scholar
[8]Philipson, C., The Swedish Systems of Bonus, The ASTIN Bulletin, Vol. 1, 1960.CrossRefGoogle Scholar
[9]Seal, H., Stochastic Theory of a Risk Business, J. Wiley and Sons, New York, 1969.Google Scholar