A remark on Wiener process approximation of risk processes

Extract

In Bohman the following model is considered. Our notation follows Bohman.

Let Z₁, Z₂, … be a sequence of independent random variables with distribution function F and put

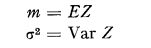
Put

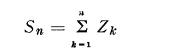
and define X by

X = inf{n; S_n > U, S_k ≤ U for k = 1, …, n − 1}.

Bohman shows that if U → ∞ in such a way that U/σ → ∞ and 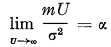then

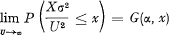
where G(α, x) is the distribution function for the time when a Wiener process X(t) with EX(t) = αt and Var X(t) = t first crosses the level 1.

Let N be an integer, which in a certain sense corresponds to “time”, and consider P(X ≤ N). This is thus the probability of ruin before the N:th claim.