Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T21:08:45.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Robust Credibility1

Published online by Cambridge University Press:  29 August 2014

Alois Gisler  and
Peter Reinhard
Alois Gisler*
Affiliation:
“Winterthur”, Swiss Insurance Company Winterthur
Peter Reinhard*
Affiliation:
“Winterthur”, Swiss Insurance Company Winterthur
*
‘Winterthur’, Swiss Insurance Company, Box 357, CH-8401 Winterthur.
‘Winterthur’, Swiss Insurance Company, Box 357, CH-8401 Winterthur.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

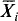Outlier observations caused by big claims or by an event producing a series of claims are a special problem in ratemaking and in tariff calculation. The authors believe that combining credibility and robust statistics is the right answer to this problem. The main idea is to robustify the individual claims experience by using a robust estimator Ti instead of the individual mean and to look at the credibility estimator based on the robust statistics {Ti: i = 1, 2, …} . Choosing a particular influence function leads to datatrimming with an observation-dependent trimming point.

Keywords

Robust statisticsstandard credibility modelsdata trimming
Type
Articles
Information
ASTIN Bulletin: The Journal of the IAA , Volume 23 , Issue 1 , May 1993 , pp. 117 - 143
Copyright
Copyright © International Actuarial Association 1993

Footnotes

1

A first version of the paper was presented at the ASTIN Colloquium 1990 in Switzerland.

References

REFERENCES

Ammeter, H. (1982) Mathematisches Modell zur Kalkulation der Tarife in der schweizerischen Feuer- und Elementarschadenversicherung. Internal Paper, available from the author.Google Scholar
Bühlmann, H. and Straub, E. (1970) Glaubwürdigkeit für Schadensätze. Mitteilungen der Vereinigung Schweizerischer Versicherungsmathematiker 70, 11–113.Google Scholar
Bühlmann, H., Gisler, A. and Jewell, W. (1982) Excess Claims and Data Trimming in the Context of Credibility Rating Procedures. Mitteilungen der Vereinigung Schweizerischer Versicherungsmathematiker 82, 1, 117–147.Google Scholar
Dubey, A. and Gisler, A. (1981) On Parameter Estimators in Credibility. Mitteilungen der Vereinigung Schweizerischer Versicherungsmathematiker 81, 2, 187–212.Google Scholar
Gisler, A. (1980) Optimales Stutzen von Beobachtungen im Credibility-Modell, ETH-Thesis Nr. 6556. See also Gisler A. (1980) Optimum trimming of data in the Credibility Model. Mitteilungen der Vereinigung Schweizerischer Versicherungsmathematiker 80, 3, 313–326.Google Scholar
Gisler, A. (1990) Credibility Theory Made Easy. Mitteilungen der Schweizerischen Vereinigung der Versicherungsmathematiker 90, 1, 75–100.Google Scholar
Hampel, F. R. (1968) Contributions to the theory of robust estimation. Ph. D. thesis. University of California Berkeley.Google Scholar
Hampel, F. R. (1974) The influence curve and its role in robust estimation. J. Am. Statist. Assoc. 69, 383–393.CrossRefGoogle Scholar
Hampel, F. R., Ronchetti, E., Rousseeuw, P. and Stahel, W. (1986) Robust Statistics. John Wiley & Sons, New York.Google Scholar
Hogg, R. V. and Klugman, S. A. (1984) Loss distributions. John Wiley & Sons, New York.CrossRefGoogle Scholar
Huber, P. (1964) Robust estimation of a location parameter. Annals of Mathematical Statistics 35, 73–101.CrossRefGoogle Scholar
Kremer, E. (1991) Large Claims in Credibility. Blätter der Deutschen Gesellschaft für Versicherungsmathematik XX, 123–150.Google Scholar
Künsch, H. R. (1992) Robust Methods for Credibility. ASTIN Bulletin 22, 33–49.CrossRefGoogle Scholar
Reinhard, P. (1989) Robuste Schätzungen im Credibility-Modell. Diplomarbeit, ETH Zürich.Google Scholar
Strauss, J. (1984) Calculation of Premium Rates according to the new German Industrial Fire Tariff 82. Proceedings of the 4 Countries ASTIN-Symposium, Akersloot, 3–21.Google Scholar