Can learning a new language make you better at maths? A meta-analysis of foreign language learning and numeracy skills during early adolescence

Abstract

This systematic review and meta-analysis explore the correlation between foreign language instruction and mathematical skills in young adolescents, highlighting the significance of high school mathematical education and the adaptability of the adolescent brain. Focused on students starting second language programs between ages 8 and 13, following PRISMA guidelines, this review included 25 studies (1978–2020) with 785,552 participants. Using a random-effects model, the overall effect size revealed a statistically significant relationship between our variables, indicating a threefold higher likelihood of passing or achieving higher grades in mathematical tests for language-learning students. Moderating variables analyses identified socioeconomic status (SES) and intervention length as influencers of observed heterogeneity, with SES being the primary factor. Sensitivity analyses, including adding potentially missing studies and removing outliers, confirmed the robustness of the overall effect. Nonetheless, additional research is needed to enhance global diversity and comprehensively understand the interplay between language learning and cognitive function.

Highlights

• • Systematic review and meta-analysis, 25 studies (1978–2020), 785,552 children.

• • Random-effects model: moderate, significant effect (OR = 2.99, p < 0.0001).

• • Mixed-effects model explained over 65% of between-study heterogeneity.

• • Sensitivity and subgroup analyses resulted in positive, significant correlations.

• • Further research is needed to identify confounding factors and enhance global diversity.

1. Introduction

Mathematics has long been considered a challenge within the educational system, often eliciting apprehension among students, administrators and government officials. This complex discipline is both feared and actively pursued in the quest for improved educational outcomes (Freeman et al., 2019). In contrast to subjects such as mathematics and science, other subjects, including foreign language learning, are seen as less critical, particularly in English-speaking countries and among schools with low socio-economic profiles across the OECD countries (OECD, 2023a). Consequently, we raise the question: What if the cognitive exercise involved in language acquisition could enhance numerical aptitude?

The significance of mathematical education, particularly at the secondary school level, is widely acknowledged as a crucial determinant of students’ academic and vocational success. Research has demonstrated a positive correlation between fundamental mathematical skills and academic achievement across various high school subjects (Anderton et al., 2017; Badru & Owodunni, 2021; Kanwal et al., 2022) and in university programs (Ballard & Johnson, 2004; Johnson & Kuennen, 2006; Yunker et al., 2009). Furthermore, proficiency in mathematics has been linked to improvements in many facets of life, including the transition between secondary school and university (Anderton et al., 2017), performance in university studies (Delaney & Devereux, 2020) and outcomes in the labour market, such as increased salaries and higher-level jobs (Joensen & Nielsen, 2009).

Over the past 15 years, the importance of Science, Technology, Engineering and Mathematics (STEM) studies has gained global recognition for its pivotal role in technological advancement, economic competitiveness and social welfare (Freeman et al., 2019). Consequently, there has been a significant increase in STEM education research in both developed and developing countries (Zhan et al., 2022). Nonetheless, challenges persist, particularly in enhancing students’ attitudes towards mathematics and facilitating mathematical learning for those who find it daunting (Tytler, 2020).

Similarly, education experts have emphasised that learning a second language offers the added social benefits of acquiring linguistic and cultural skills, which have become increasingly crucial in today’s globalised and multicultural society (Davies, 2018; Midgley, 2017). Research has also demonstrated that acquiring foreign language proficiency can open up better job opportunities (Araújo et al., 2015). However, students do not always perceive foreign language learning as a valuable asset for their future careers and studies, especially when considering local or domestic employment opportunities (OECD, 2020).

As such, if there is a positive correlation between language acquisition during high school years and mathematical skills, this may help boost teenagers’ perception of learning a second language as a complementary method to improve their mathematical achievement.

1.1. Second language learning

The acquisition of a second language (L2) and the factors influencing one’s success in this endeavour have been extensively studied. Historically, the literature was dominated by the critical or sensitive period hypothesis, which suggested that achieving native-like proficiency in an L2, particularly in pronunciation and grammar, becomes nearly impossible after early childhood (Johnson & Newport, 1989; Scovel, 1988).

However, this theory has encountered challenges on three main fronts. Firstly, recent studies indicate that if there is indeed a sensitive period for L2 learning, it extends beyond the previously assumed boundaries, continuing until approximately 17 to 18 years of age (Hartshorne et al., 2018; Master et al., 2020). Secondly, researchers have demonstrated that differences in cognitive ability, the context in which language is acquired and even native language, rather than one’s age, play the most significant role in achieving native-like proficiency (Bialystok & Hakuta, 1999; Birdsong, 2006; Figueiredo et al., 2016; Flege et al., 1999; Hakuta, 2001; Hakuta et al., 2003), even when it comes to phonology (Abu-rabia et al., 2004; Birdsong, 2006; Darcy et al., 2015). Finally, the advent of neuroimaging techniques has provided evidence indicating that the brain’s plasticity during the early stages of adolescence bears notable similarities to that observed during the first three years of life (Fuhrmann et al., 2015; Selemon, 2013; Steinberg, 2014), possibly rendering it well-suited for the acquisition of new languages. This heightened plasticity is further enhanced by the advantages conferred by white matter growth and pruning, ultimately leading to heightened cognitive efficiency (Selemon, 2013; Simpson-Kent et al., 2020; Squeglia et al., 2013).

1.1.1. Second language learning and cognitive ability

The effect of L2 acquisition on cognition has been a topic of intense debate for over a century. Initially, bilingualism was seen as a cognitive burden (Darcy, 1953; Saer, 1923). Later studies, however, highlighted the cognitive advantages of bilingualism (for a timeline see Barac and Bialystok (2011)). Nonetheless, some researchers argue that the evidence supporting bilingualism’s impact on executive control is inconsistent (Andreou et al., 2020; Dick et al., 2019; Paap et al., 2015; Paap & Sawi, 2014).

A current theory proposes that the inconsistency in results regarding bilingualism arises from its dynamic nature (Beatty-Martínez & Titone, 2021; Bialystok & Craik, 2022; Di Pisa et al., 2021). Bilingualism evolves based on factors like duration and intensity of language learning and usage, which lead to variations in brain changes (Pliatsikas et al., 2020) and subsequent non-linguistic cognitive benefits (DeLuca et al., 2019, 2020; Gullifer et al., 2018).

Although most of the research has studied the advantages that bilingualism may confer, some researchers have sought to determine the level of language mastery needed to activate these benefits. Neuroimaging studies have shown that even early stages of L2 learning can induce brain changes, such as grey matter density and white matter integrity, observable across all ages and sensitive to variables like age of acquisition and performance level (Li et al., 2014). These changes could be seen after just three months of language training, and since brain changes have been associated with executive control enhancement (Luna et al., 2015), the author speculated that these brain changes might result in enhancing executive functions (EFs).

Consistent with this hypothesis, studies have found that language learners exhibited EF scores lower than early or simultaneous bilingual but higher than any monolingual speaker groups (White & Greenfield, 2017). However, others found that no significant gains were achieved when the L2 input was too limited (Poarch & van Hell, 2012). These differences may be explained by Bialystok and Barac’s (2012) and Sorge et al. (2017) work on language learners, which proposes that the interaction between language learning and executive functioning is largely dependent on the learners’ language use and exposure.

1.2. Mathematical ability and learning

Mathematical ability is defined as the capacity to learn, apply and retain mathematical theories and ideas, enabling effective problem-solving in any numerical context (Karsenty, 2014). Despite changes in teaching techniques, the core mathematical content remains consistent. Davis (1978) identified four fundamental areas of mathematical knowledge, which continue to be the main focus of math education, aiming to facilitate students’ understanding:

Mathematical Concepts: Basic knowledge, like counting or arithmetic (e.g., addition, or subtraction).

Mathematical Generalisations: Patterns or relationships between numbers or basic knowledge, such as the distributive law or recognising that adding two odd numbers will always result in an even number.

Mathematical Procedures: Sequence of mathematical operations carried out in order, like BIMDAS (Brackets, Indices, Multiplication, Division, Addition and Subtraction) for solving algebraic equations.

Number Facts: Simple calculations between two numbers, usually committed to memory, such as 5 + 5 = 10, or 4 × 5 = 20.

At high-school level, the context of this review, these areas come together to help students acquire fundamental numerical knowledge (e.g., counting, magnitude, etc.), understand arithmetic, geometry and algebra and develop proficiency in mathematical word-problem solving and reasoning (Peng et al., 2015). To assess these mathematical skills, most tools include common measures such as basic operations (i.e., arithmetic), algebra, geometry, mathematical word problems, logic and reasoning and practical applications (Breaux & Lichtenberger, 2016; Brown et al., 2012; Hresko et al., 2003).

With advancements in brain imaging and neuroscience, the focus has shifted from teaching methods to understanding how students learn. Geary (2004), for example, observed that learning disabilities often stem from deficits in knowledge competencies, linked to disruptions in neural structures related to the Central Executive (EF – inhibitory control, cognitive flexibility, working memory), the Language System (phonetic–articulatory system) or the Visuospatial System. This understanding has led to a framework suggesting that EF plays a critical role in mathematical learning and may predict numerical ability.

1.2.1. Mathematical learning and cognitive ability

Mathematics is the academic domain with the most robust and consistent correlation with cognitive ability across all age groups. A longitudinal study of 562 four-year-old children found that central executive skills (inhibitory control, attention flexibility and working memory) were more strongly associated with mathematical achievement than with literacy (Fuhs et al., 2014). Similarly, cognitive flexibility has been shown to predict mathematical performance in elementary school students aged seven to ten (Cantin et al., 2016) and in adolescents (Gathercole et al., 2004).

Diverse methods have been used to study the relationship between cognitive skills and mathematics (for reviews see Bull and Lee (2014) and Cragg and Gilmore (2014)). Some studies combine EF processes into one latent variable, finding a significant positive association with math performance, particularly during early childhood (Fuhs et al., 2014; Mazzocco & Kover, 2007; Mercader et al., 2018). However, this correlation weakens with age, potentially because different cognitive processes relate to different mathematical skills at different ages, reducing the overall effect of the latent variable (Bull & Lee, 2014).

Other researchers measure EF processes separately to match them independently to mathematical performance. For instance, it has been suggested that base levels of inhibitory control skills and their growth positively predicted children’s early math skills (Choi et al., 2018). Conversely, lack of inhibition was highly correlated with poor mathematical ability in children aged six and eight years (Bull & Scerif, 2001). A meta-analysis found a substantial and significant relationship between cognitive flexibility and math (Yeniad et al., 2013). Additionally, working memory, both visuo-spatial and verbal, has also been closely related to mathematical ability, often showing a stronger association than with other central executive processes (Lin, 2018; St Clair-Thompson & Gathercole, 2006).

1.3. Language learning and mathematical ability: The role of executive function

The effect of bilingualism on specific EF skills, namely inhibition (ability to control rehearsed or automatic behaviours), cognitive flexibility (ability to switch tasks or strategies when problem-solving) and working memory (mental manipulation of recently acquired information) (Miyake et al., 2000), has been extensively studied. Similarly, the link between cognitive processes and mathematical ability has been the aim of numerous studies. However, the specific cognitive skills that enhance individual math skills remain unclear, and only some general interactions between these variables have been identified.

1.3.1. Inhibitory control

Studies have shown that bilinguals exhibited faster response times and less interference in trials with and without conflicts when compared to monolinguals, even among very low SES individuals without literacy skills (Barac et al., 2014; Nair et al., 2017; Poarch & van Hell, 2012). Additionally, Planckaert et al. (2023), in their systematic review, found a higher prevalence of the bilingual advantage in inhibition and switching tasks among children under six years of age, suggesting this advantage may diminish as children advance in age.

Inhibitory control is crucial for solving mathematical word problems and, to a lesser extent, for basic number knowledge and arithmetic. Mathematical word problems often include extraneous information, and the ability to disregard irrelevant information is essential for finding the correct answer (Bull & Lee, 2014). Inhibitory control aids in managing order of magnitude, particularly in fractions, by helping to suppress incorrect automatic responses (e.g., recognising that 1/2 is larger than 1/10, despite 10 being larger than 2) (Bull & Lee, 2014; Nguyen et al., 2019). It also helps with the correct application of order of operations in arithmetic, preventing students from solving equations in the sequence they appear (e.g. 1 + 2 × 3 − 2 = 7 rather than 5, which is the correct response) (Nguyen et al., 2019).

1.3.2. Cognitive flexibility

Barac et al. (2014) concluded in their review that cognitive flexibility, along with inhibition, were the EF processes with the most robust reported advantages for bilinguals. This conclusion is supported by previous studies, such as Barac and Bialystok (2012), which showed that bilinguals outperformed their monolingual peers in task switching, regardless of language similarity, cultural background or language of schooling. Additionally, Adi-Japha et al. (2010) found that the enhancement of shifting skills due to bilingualism extends to cognitive flexibility in non-linguistic domains.

Cognitive flexibility or shifting, is hypothesized to be linked to high performance in algebra, word-problem solving and mathematical reasoning. Complex algebraic exercises and mathematical word problems require multiple steps to be solved, and each step may require a different approach. Thus, a heightened ability to switch between solving strategies is associated with achievement in these areas (Bull & Lee, 2014; Cragg & Gilmore, 2014; Nguyen et al., 2019).

1.3.3. Working memory

Blom et al. (2014) and Morales et al. (2013) found that bilingual children outperformed their monolingual counterparts in working memory, especially when the tasks were more demanding (Morales et al., 2013) and even when the children were socioeconomically disadvantaged (Blom et al., 2014). More recently, meta-analyses performed by Grundy and Timmer (2016) and Monnier et al. (2022) showed a significant small to medium effect size favouring an advantage due to bilingualism, which appeared more frequently in children, and was largely moderated by the language in which the tasks were performed.

Some authors have found conflicting results. For instance, Antón et al. (2019) observed no disparity between monolingual and bilingual individuals in simple working memory tasks (e.g., remembering visuospatial patterns). However, when more complex tasks were introduced (e.g., remembering and reversing a string of numbers), bilinguals exhibited a distinct advantage over their monolingual counterparts, even after controlling for known confounding variables.

Working memory has been extensively correlated with mathematical performance, particularly with arithmetic and mathematical word-problem solving. Bellon et al. (2019) found that updating accuracy predicted arithmetic accuracy, as working memory is necessary for recalling arithmetic facts and storing interim solutions. Moreover, single and multi-digit calculations were found to rely on working memory, regardless of the operation required to arrive at the solution (Peng et al., 2015). Interestingly, the reliance on working memory for solving basic operations decreases with age; children depend more on working memory for these tasks than adults do (Cragg & Gilmore, 2014).

Additionally, working memory significantly influences mathematical word-problem solving, indicating that this skill does not solely depend on language-based working memory resources as previously thought (Peng et al., 2015).

1.4. Language learning and mathematical ability in adolescents: Is there a link?

As evident from the substantial body of research linking both language learning and mathematical ability to the central EF, the idea of exploring the potential of learning new languages to enhance mathematical achievement is indeed grounded in empirical evidence.

While there is research to support this hypothesis, it is important to note that only a relatively small number of researchers have explored this topic, and the majority of these investigations have primarily centred on preschool-aged children, such as those conducted by Choi et al. (2018) and Hartanto et al. (2018), as well as primary school children, as evidenced by the studies of Iqbal (2022) and Stewart (2005). This tendency may be attributed to the heightened neuroplasticity observed during these developmental stages. Interestingly, the findings from these studies have consistently demonstrated affirmative outcomes.

For instance, Hartanto et al. (2018) examined the correlation between bilingualism and mathematical achievement, employing various metrics, including teacher evaluations, emergent numeracy skills and standardised test scores. Their research revealed that bilingualism positively contributed to children’s mathematical aptitude and reasoning abilities, after controlling for potential confounding variables like age, gender and socio-economic status. Similarly, Choi et al. (2018), in their investigation involving low-income preschoolers, discovered that bilingual children exhibited superior performance in mathematics assessments when compared to their monolingual counterparts, even in cases where bilingual children started with lower base skills. Furthermore, both literature reviews conducted by Stewart (2005) and Iqbal (2022), which focused on primary school children, highlighted a positive association between bilingualism and foreign language acquisition and heightened mathematical ability, as indicated by higher achievement test scores.

Given the recognition that early adolescence may represent a period of heightened neuroplasticity and central EF changes (Luna et al., 2015; Steinberg, 2014), it is reasonable to build up on existing research and investigate the possibility of a positive association between second language learning and mathematical ability among adolescents.

1.5. Research question

Recognising the significance of mathematical education during high school and the potential of the adaptable adolescent brain, we chose to focus our study on students who initiated their second language programs at around 8–13 years of age, which includes the onset of early puberty as defined by Dorn et al. (2006), and were tested during secondary school years.

Thus, we carried out a systematic review and meta-analysis to answer our research question: Do young adolescents who received formal instruction in a foreign language exhibit improved numerical skills compared to those who did not?

2. Method

This systematic review was conducted and reported using the guidelines set out in the Johanna Briggs Institute (Aromataris & Munn, 2020) and the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) statement (Page et al., 2021). Our protocol was registered with PROSPERO, under the ID: CRD42020172859.

2.1. Search strategy

For this review, studies were identified by searching electronic databases (PsycINFO, PubMed, ERIC, Wiley Online Library, EBSCOhost, Taylor and Francis online and Scopus) and grey literature (EMBASE, Web of Science, MedNar) for published peer-reviewed journal articles, reports, and books, as well as unpublished masters’ theses, doctoral dissertations, conference proceedings and presentations. Article alerts from relevant databases were also monitored to identify peer-reviewed papers.

The search terms were derived from the PICO protocol, and depending on the database, a combination of subject headings (MeSH), keywords and wildcards was used to ensure the search criteria were robust. Each search consisted of all the terms linked using Boolean operators, limited by language (English only, due to the difficulty of the authors to extract data from papers in other languages) and type of publication (only journal articles, reports, dissertations, books, speeches and conference proceedings were included) with no restrictions of date of publication.

The searches were performed between August and November 2022, while the search alerts were monitored until the end of December in the same year (2022). Additional information is provided in the Supplementary Materials. The search terms and an example can be found in Table S1 (Appendix S1). The complete list of retrieved articles is available in Appendix S2.

2.2. Inclusion and exclusion criteria

All studies that met the following criteria were considered to answer our research question and were included.

2.2.1. Types of study

All types of studies reported in English that explore the quantitative relationship between language learning and academic achievement (i.e., in numeracy, mathematics or science).

2.2.2. Participants/population

Participants were typically-developing early adolescents (including children from 9 to 17 years of age) enrolled in a formal school program.

2.2.3. Intervention(s), exposure(s)

Participants in the study were required to engage in a formal foreign language learning program, either within a school setting or through alternative means, where the second language was not the exclusive medium of instruction. It is important to highlight that, for inclusion in the study, students must have received explicit instruction on the structural aspects of the second language (such as grammar and sentence formation), as opposed to mere exposure to the language. Consequently, the research focused on examining the impact of bilingual education (BE), dual language (DL) and two-way bilingual (TWB) programs initiated during elementary education, where fundamental language skills are taught.

A brief explanation of the interventions within the included studies is provided below.

1. a. Transitional Bilingual Education (TBE): A US-based program where students are taught English as a Second Language (ESL) while learning subjects like math or science in their native language until their English proficiency is sufficient for them to function successfully in the mainstream ¹ with additional support classes (Medina et al., 1985).

2. b. Two-Way Bilingual Education Program Model (TWB): This US bilingual education model uses both Spanish and English as the medium of instruction, maintaining a 50/50 to 60/40 ratio between Spanish and English-speaking students since its inception in 1993. Instruction in literacy, math, science and social studies alternates weekly between Spanish and English (Cobb et al., 2006).

3. c. Bilingual Education (BE) Program: Designed for native speakers of languages other than English with limited English proficiency, this program aims to prepare students for success in mainstream classrooms while maintaining access to their native language. Instruction is provided in two or more languages, with the amount of instruction given in each language varying by school. Prior to 1995, it operated as a traditional transitional bilingual education (TBE) program, focusing on exiting within 3 years (de Jong, 2004).

4. d. Dual Language Bilingual Program (DL): A program, implemented in the US, where roughly equal numbers of English learners and fluent/native English-speaking students are taught together, offering a higher percentage of instruction in Spanish. The goal is full bilingualism and biliteracy for both groups (HISD, 2020).

5. e. English as a Second Language Program (ESL): A self-contained program focusing on English mastery to prepare students for success in an English-speaking environment. Students typically divide their day between regular English classes and specialised ESL instruction (de Jong, 2004).

6. f. Foreign Language Learning (FL): This program enables students to learn a non-native language outside of the geographical area where it is commonly spoken (e.g., learning French in the UK) (Karaoglan Yilmaz et al., 2020).

Notably, conventional high school programs lacking second language education (or support for immigrant students) and bilingual programs commencing in high school were excluded from our review.

2.2.4. Outcome(s)

Any studies reporting short or long-term academic achievement, regarding numerical skills, ability, reasoning, competence, achievement, or performance measured quantitatively (e.g., results from standardised mathematics tests, such as SAT) were included. Qualitative studies, or those which did not report on numerical achievement, were not considered.

Therefore, studies were excluded if they

1. a. did not provide quantitative results (e.g., editorials, qualitative studies);

2. b. were not fully available in English, even if the abstract was;

3. c. reported on performance on skills/subjects that are not numerical (e.g., English literature, music, sports);

4. d. reported on the current academic performance of students who were being taught in a second language (e.g., foreign students in conventional schools) or

5. e. included a sample specifically selecting students diagnosed with any form of atypical development that could affect their learning (e.g., language delay).

Once all titles and abstracts were collated, each team member reviewed a set of ten. To ensure a high level of inclusion/exclusion agreement, the results of this set were discussed, and following this discussion, all the authors independently reviewed a second set of ten titles and abstracts. As the agreement among the team reached 85%, the selection continued.

All studies (title and abstract) were uploaded to Rayyan (Ouzzani et al., 2016), where they were screened by at least two independent reviewers, working in blind mode, unable to see other reviewers’ decisions. A 95% agreement (Cohen’s kappa 0.57) was reached in screening. Following this, reference lists of related articles were checked, and a Google Scholar search was conducted to ensure the search was exhaustive. This process identified 71 new studies (a complete list is provided in Appendix S3), which were also reviewed independently by two team members (96% agreement, Cohen’s kappa 0.85). Both times, areas of disagreement were resolved by a third team member. Common areas of disagreement involved the availability of data to analyse (Olsen & Brown, 1992) and misinterpretations concerning the start of interventions (Padilla et al., 2022).

A total of 58 studies were retrieved to be read in full and assessed for eligibility. Ultimately, 25 studies were selected to be included in this review. The number of results obtained and reasons for exclusion can be found in the PRISMA flowchart (Haddaway et al., 2022) (Figure 1).

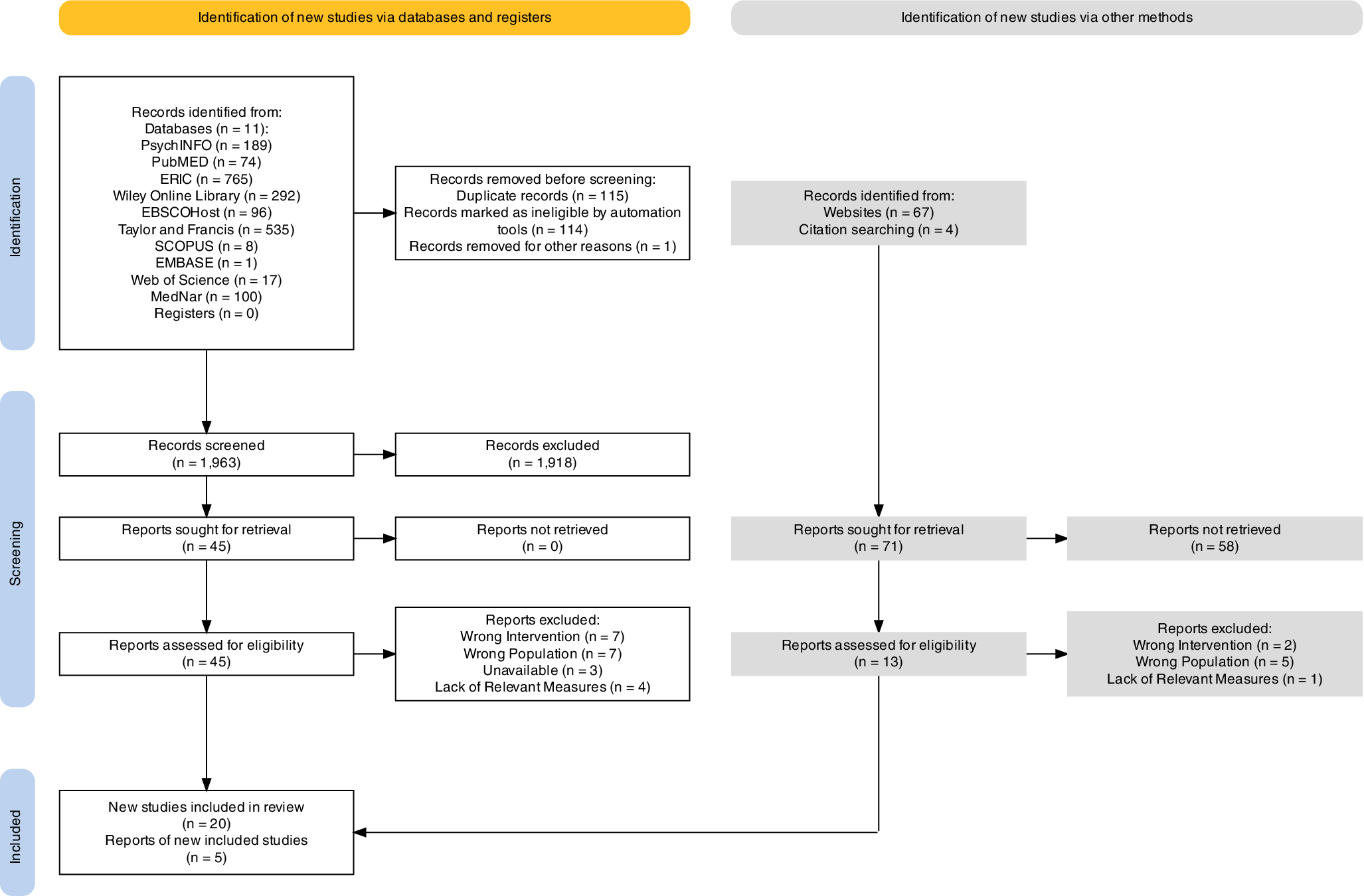
Figure 1. PRISMA Flowchart.

2.3. Data extraction

A data extraction sheet was developed to record relevant data from the selected studies. This included the study description (author, title, year, type and location,), population characteristics (description, participant number, gender, SES, age at the time of testing and languages), methods (aim, intervention type and duration), outcomes (assessment tools, their scale and confounding variables) and results (primary and other significant findings, statistical method and effect size). Conclusion and limitations for each study were also documented.

Eligibility and Risk of Bias (ROB) columns were included: eligibility ensured adherence to the selection criteria (intervention, population and outcomes), while ROB shows the results of the ROBINS-I tool results, as well as conflict of interest and sample size bias.

Where necessary, data reported within each paper was segregated into separate results; when a study presented multiple results, the information extracted for each result was recorded in a separate row, labelled with a letter after the article ID (e.g., 4a and 4b represent two different outcomes included in Cobb et al. (2006)). As such, a total of 49 results were identified and recorded.

Two team members independently extracted data, followed by a collaborative risk of bias assessment. This assessment aimed to evaluate study quality but did not exclude any studies. Consensus on critical studies was achieved through thorough discussions. The detailed results of the ROBINS-I tool and the data extraction sheet are available in Appendices S4 and S5.

2.4. Publication bias and small study effect

Although great care was taken to include all the available literature on our topic, there remains a concern about publication bias, where studies with significant results tend to be published more frequently than those which do not (Cooper, 2017). To evaluate the prospect of publication bias, a contoured enhanced funnel plot was generated following the methodology outlined by Peters et al. (2008). This approach aimed to discern any bias against statistically non-significant results.

Moreover, for a quantitative assessment of potential bias, both Trim and Fill analysis and random/mixed effect Egger’s tests were employed (Rothstein et al., 2005). These analyses were conducted to gauge and address any potential impact of bias on the overall findings.

2.5. Statistical analyses

2.5.1. Effect size calculations

The selected primary studies documented the impact of language learning on numerical skills using diverse methods, encompassing various formats of statistical analyses such as t-values, F-values exclusively, F-values in conjunction with p-values and Cohen’s d, or by providing descriptive data. We transformed all these statistics into odds ratios (OR), a measure of effect size that shows the strength of the association between exposure and target event due to its ease of calculation and interpretation (especially true in in its logarithmic form) (Norton et al., 2018).

To ensure the fulfilment of the independence assumption for all results recorded during the data extraction stage, we verified they were obtained using different participants, outcome tests or age groups. This led to removing outcomes from studies where either the sample had been used in previous analyses or had been pooled to produce an overall effect. Additionally, some studies provided outcome data on several samples, but the available information did not suffice to calculate individual effect sizes; in these cases, the data were combined across the samples. Such is the case of the work by de Jong (2004), which did not provide precise information on their control group, making it impossible to calculate individual effect sizes for the samples studied (i.e., year 4 and 8).

If there was sufficient data to directly calculate ORs (and log ORs), we recorded the number of students who had the treatment (i.e., foreign language learning) and those who had not (control group), as well as those who had achieved a passing mark on the outcome instrument (i.e., mathematical skills test), and those who failed to create 2 × 2 tables (see Table S2 in Appendix S1 for an example). Then, the R package ‘metafor’ (Viechtbauer, 2010) was used to compute ORs (logORs) and variances.

When the study data was in a continuous format, and there was insufficient information to directly calculate ORs, Cohen’s d and variances were computed instead (Lipsey & Wilson, 2000; Wilson, 2023). The resulting effect sizes were converted into logORs, following the mechanism, and associated statistical formulae, described by Borenstein et al. (2009) (for additional information, see Figure S1 in Appendix S1). Calculations and results are available in Appendix S6.

2.5.2. Moderating variables

During the process of data extraction, certain variables were identified as potential moderators due to their possible influence on the reported results and their availability in the data. These variables included the type and duration of the intervention (measured in years), the socio-economic status of the treatment group (as reported), the age of the participants at the time of testing, the type of publication, the type of outcome tests used, the gender distribution (as percentage of females) and whether the first language spoken by the control group was the dominant language or not (e.g., for studies in the USA, control groups comprised of native English speakers, native Spanish speakers or both native Spanish and English speakers).

While all variables were directly extracted from the study content, simplifications were necessary for modelling. For instance, intervention types were grouped into BE programs (balanced instruction in both first and second languages) and Second/Foreign language programs (mainly second language instruction). Similarly, 16 types of mathematical skills tests were categorised into standardised and non-standardised tests, depending on their reach and application. A summary of the coding strategy is provided in Table S3 of Appendix S1.

2.5.3. Meta-analytical models

All meta-analytical analyses were conducted using two R packages: ‘metafor’ (Viechtbauer, 2010) and ‘meta’ (Balduzzi et al., 2019). Because of the substantial variation in population characteristics (such as age, native and second language), intervention designs (e.g., length and type of language programs) and outcome measures (different types of mathematical skills tests) across studies, and given the assumption of the absence of a ‘true’ effect size (Borenstein et al., 2009), we opted for a random-effects model to aggregate the calculated effect sizes and estimate an overall effect size.

We utilised the restricted maximum likelihood (REML) estimation to estimate the heterogeneity variance. This choice was based on the literature’s suggestion that it produces almost unbiased results (Langan et al., 2019; Tanriver-Ayder et al., 2021; Viechtbauer, 2010). To test individual coefficients and their confidence intervals, we applied the Hartung, Knapp, Sidik and Jonkman (HKSJ) method, which has received widespread recommendations, especially when the number of studies is small (Balduzzi et al., 2019; IntHout et al., 2014; Viechtbauer, 2010).

To assess between-study heterogeneity, we used the I ² statistic, reported as a percentage of the variability in effect sizes (Higgins et al., 2023). A high level of variability in effect sizes, unrelated to sampling error, was expected. To explore this heterogeneity, we constructed a mixed-effects model. We individually tested moderating variables to examine their impact on between-study variability. Significant variables were then incorporated into the model, which we subsequently tested for their relative contribution (Borenstein et al., 2009). The R code and the data input are available in the Supplementary Materials, in Appendices S7 and S8, respectively.

3. Results

3.1. Systematic review

Out of the selected 25 studies, published between 1978 and 2020, 44 individual results were extracted (see Table 1 for details). A total of 785,552 children were included in the analysis; 91,997 were language learners, while 690,555 were in the control groups. Sample sizes ranged from 6 to 47,844 for the language learning group (Me = 58) and 6 to 281,642 for the control group (Me = 9,877.5). The age range of the participants at the time of the study spanned from 10 to 17 years (M = 13.97, Me = 13.5, Std Dev = 1.63), while the duration of the interventions ranged from 1 to 7 years (M = 3.65, Me = 4).

Table 1. Systematic review results summary

* Houston Independent School District (HISD) census information show that around 58-60% of the population in those years were economically disadvantaged, while the rest were predominantly middle class.

Regarding study design, 54% of the effect sizes were from secondary analyses of existing data. Quasi-experimental studies contributed 18% of the effect sizes, while cross-sectional surveys accounted for 11%. Experimental studies represented 9% of the effect sizes, and longitudinal quantitative studies contributed 7% to the overall dataset.

Concerning the nature of interventions implemented, 14% of the studies used Second/Foreign Language programs (English as Second Language and Foreign Language), whereas the remaining 86% of interventions were characterised as Bilingual programs (Transitional Bilingual Education, Bilingual Education, TWB Education and DL).

The participants’ linguistic backgrounds were somewhat homogeneous, as 34% of the interventions reported including only native Spanish speakers as the language learners, with English as the second language, while 48% of the studies involved both Spanish and English native speakers in a DL setting. Additionally, 7% of the studies included language learners with multilingual background, with nearly 50 different home languages recorded including Spanish, Bosnian, Vietnamese, Portuguese, Chinese, Hindi and Japanese, all learning English as a second language. Furthermore, 9% of the studies reported results on English native speakers, learning a variety of modern languages, including Spanish, French and Italian. The remaining 2% of the studies involved native Korean speakers learning English as a second language.

All studies reported results based on assessments conducted as part of the students’ school activities. The tools, such as Renaissance Star 360® Maths (RenaissanceLearning, 2024) and STAAR (TEA, 2024) tests, used by the selected studies covered fundamental mathematical domains, including number properties and operations, measurement, geometry, data analysis and probability, as well as algebraic thinking and problem-solving. While a substantial array of tests was used, with at least 16 assessments identified, most of these assessments (77%) were standardised tests, such as the Stanford Achievement Test (SAT), RS 360 Maths and STAAR tests, mandated for use across all schools within the country or state where the evaluation occurred. The remaining results were derived from assessments conducted at district level (5%) or within individual schools (18%).

3.2. Overall effect and between-study heterogeneity

As previously explained, a random-effects model was used to aggregate the computed effect sizes and estimate the overall effect of language learning on mathematical skills. This model yielded a moderate and statistically significant effect size of 1.09, 95% CI = [0.75, 1.44], p < 0.0001 (see Figure 2). When converted back to ORs, this result suggests that, following the treatment, students engaged in language learning exhibited an approximately threefold increased likelihood of attaining a passing grade (or achieving higher results in standardised tests) than their peers, who were not involved in language lessons, as observed in their performance on mathematical skills tests.

Figure 2. Forest plot for the effect of foreign language learning on mathematical skills: Studies are denoted by square symbols and horizontal lines, indicating their effect size and confidence intervals respectively. The size of the squares is proportional to the weight of each study within the model, reflecting their sample size. The central position of the diamond shape conveys the overall effect, while the 95% confidence intervals are represented by the horizontal extents of the diamond’s corners.

Figure 2 shows the distribution of effect sizes from the selected studies, accompanied by their respective 95% confidence intervals. The dotted reference line, positioned at a log OR of 0, serves as a benchmark for no discernible difference in the outcomes of the mathematical skill tests. Consequently, all effect sizes situated to the right of this reference line indicate outcomes that favour the treatment, while those on the left depict results that favour the control group.

Adopting a random-effects model was deemed appropriate due to the considerable variability in effect sizes observed across the selected studies (Borenstein et al., 2009). This choice was further justified by the substantial heterogeneity detected (Q ₄₃ = 5251.99, p < 0.0001, τ² = 1.05 SE = 0.27), as well as the high degree of total variability in the true effects, I ² = 99.31%.

3.3. Analyses of moderating variables

Given the high level of heterogeneity exhibited in the random-effect model, a mixed-effect model was used to investigate the roles of the selected moderating variables. Their effects were assessed individually, as summarised in Table 2.

Table 2. Mixed-effect model: Individual variables assessment

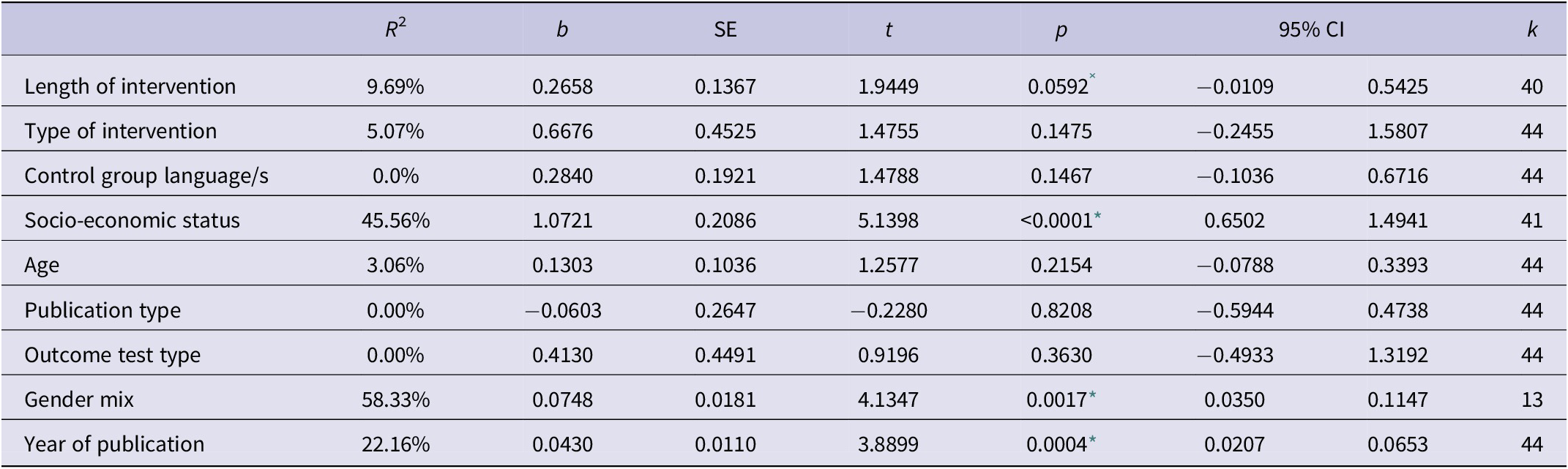
Moderating variables analyses. R² refers to the amount of heterogeneity accounted for per moderator, and b is the variation relative to the combined effect.

* Statistically significant result (p < .05).

^˟ Approaches statistical significance.

Four of the nine variables analysed demonstrated an explanatory impact on the heterogeneity. Interestingly, gender emerged as the most influential factor, contributing to 58.33% of the observed differences in effect sizes. This indicates that studies with a higher proportion of female students reported larger effect size (Figure 3D). However, it is essential to highlight that this metric was derived from approximately a quarter of the studies (n = 13), underscoring the need for a cautious interpretation of this finding.

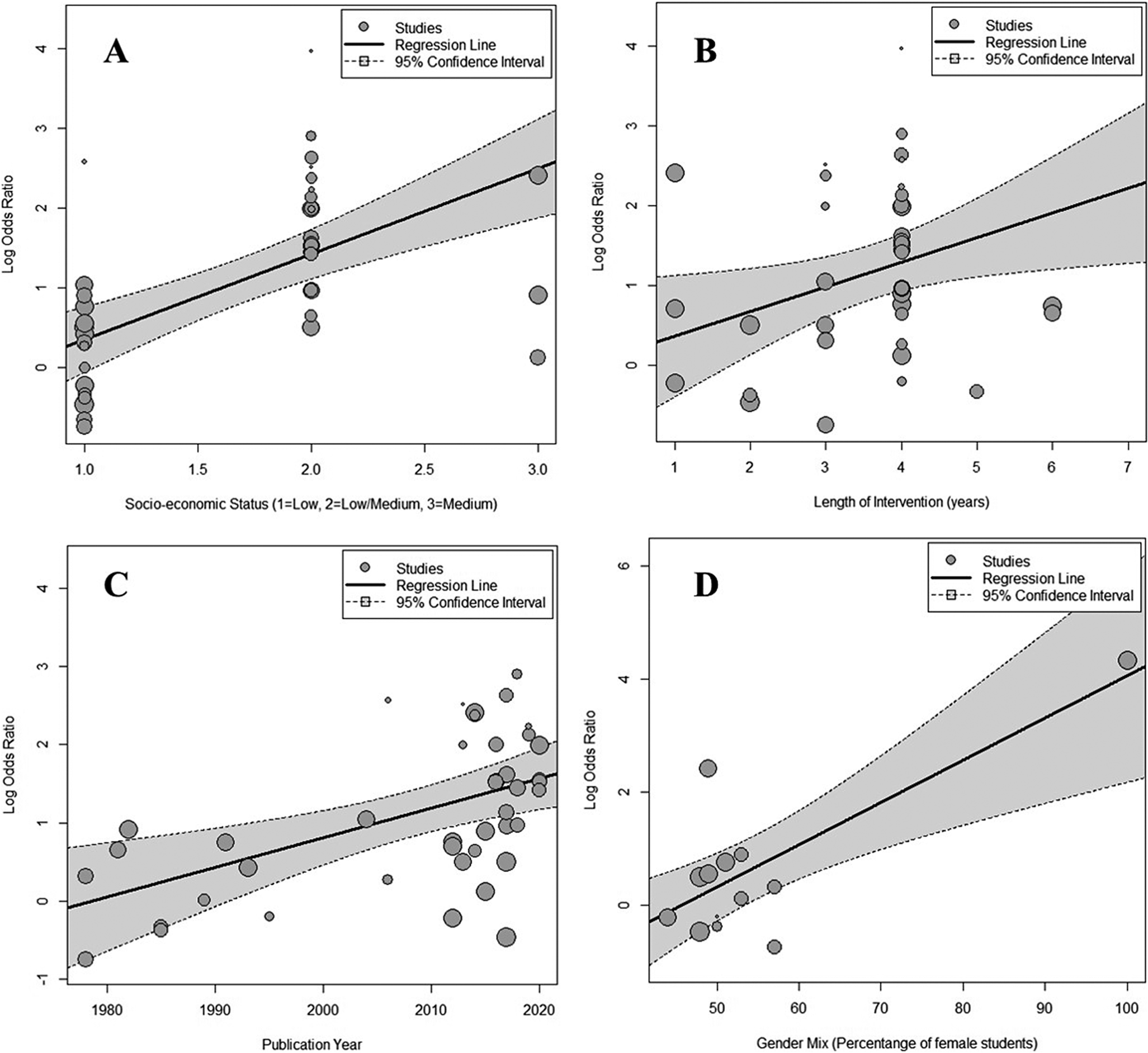
Figure 3. Moderating variables bubble plots, (A) SES, (B) Length of intervention, (C) Publication year, and (D) Gender mix. Each bubble represents a study, with its size proportional to its weight in the model, indicating the sample size. The regression line depicts the predicted Log OR as a function of each moderator, accompanied by 95% confidence intervals represented by the surrounding grey area.

Among the remaining statistically significant results, the impact of socioeconomic status (SES) (45.56%) and the length of the intervention (9.69%) were observed. SES is commonly acknowledged as a crucial influencing factor, given its association with adverse effects on educational outcomes, often observed in schools or children with lower socioeconomic levels (OECD, 2019). This pattern was observed in the current study, with a larger effect size reported among studies that examined students from higher SES background (Figure 3A). Similarly, the results indicate there is a relationship between the length of the intervention and improved outcomes (Figure 3B), aligning with the notion that longer interventions yield more favourable results.

The observed effect for the year of publication (Figure 3C) raises the possibility that recent years may exhibit a bias towards publishing research with positive and significant correlations (see Section 3.4 for further details). However, it is also possible that a cluster of studies with similar results is influencing the data. While this inference is not conclusive, it prompts a discussion on the potential effect of subsets on the overall combined effect. A further analysis on this point is presented below.

Next, a mixed-effect model incorporating all relevant variables was constructed to gain a comprehensive understanding of the data. Nevertheless, the presence of collinearity needed to be reviewed; hence, Pearson’s correlations were computed among the relevant variables (Olivoto, 2020). No significant collinearity concerns emerged with the exception of Gender mix, which exhibited a strong correlation with both outcome test type (r = 0.98, p < 0.001) and length of intervention (r = 0.78, p < 0.01). Consequently, gender mix was omitted from the mixed-effect model (see Figure S2 in Appendix S1 for details).

The constructed mixed-effect model successfully explained a considerable proportion of the observed heterogeneity (R ² = 66.16%) using most of the effect sizes in the meta-analysis (k = 38).

Nevertheless, a significant residual between-study variance persisted, as indicated by the results of the residual heterogeneity test (QE₂₉ = 153.08, p < 0.0001), signifying unaccounted sources of variability.

In this model, both the SES and the publication year maintained their statistical significance, as indicated in Table 3. Furthermore, the length of the intervention, which exhibited a near-significant association in isolation, achieved a p-value of 0.0397 in the multivariate model, thereby solidifying its role as a significant factor in the correlation between language learning and mathematics.

Table 3. Mixed-effect model: All non-correlated variables

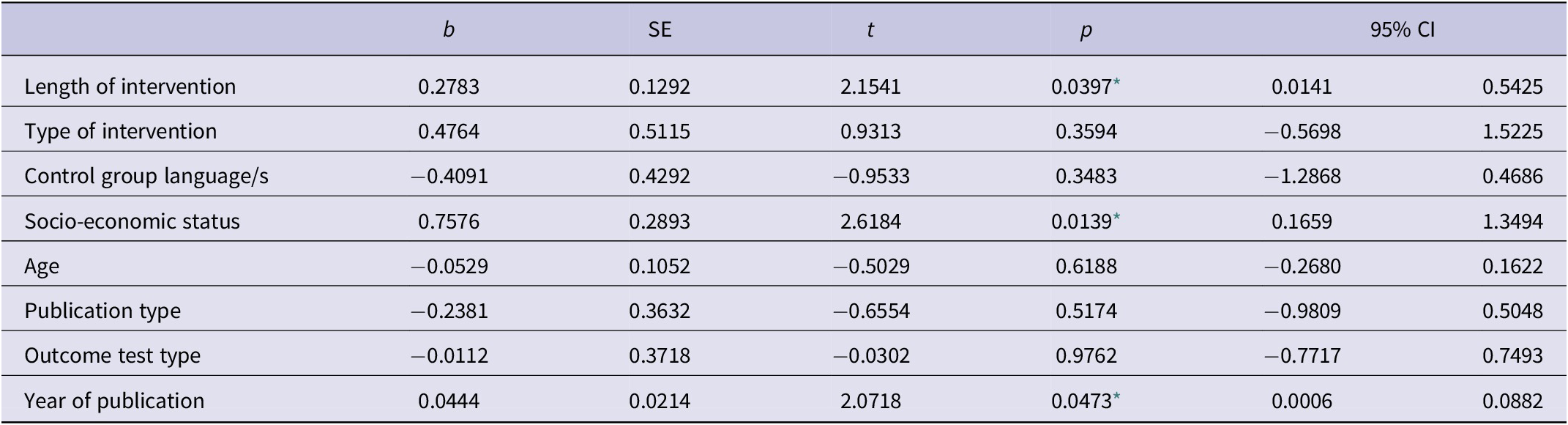
Moderating variables analyses. R² refers to the amount of heterogeneity accounted for per moderator, and b is the variation relative to the combined effect.

* Statistically significant result (p < .05).

The observed result concerning the year of publication may stem from a concentration of studies from the same source. As shown in Figure 1, a series of studies was produced by the Houston Independent School District (HISD) between 2013 and 2020. A follow-up analysis was conducted to examine whether this subset of relatively more recent studies differs significantly from other studies included in the review, utilising the same model characteristics employed for the total sample.

In the case of the HISD studies (k = 21), the applied model yielded an estimate of 1.59 (p < 0.0001) with low heterogeneity (I ² = 49%). Relatively small heterogeneity makes sense as these studies adhered to a consistent methodology, including factors such as the type and duration of intervention, as well as the nature and timing of outcome tests. In contrast, for the non-HISD studies (k = 23), the pooled effect size was smaller but still positive and statistically significant (estimate = 0.61, p = 0.0206). However, it is important to note that the heterogeneity within this subgroup was considerably higher (I ² = 99%), as anticipated due to variations in intervention approaches, participant age and types of outcome tests. As such, the findings of this analysis provide a potential explanation for the moderating role of the year of publication. It suggests that studies from HISD in recent years tended to report larger effect sizes, signifying that this trend was not solely a result of the year of publication.

3.4. Publication bias analyses

Our study employed multiple methods to assess the potential impact of publication bias on the estimated overall effect. One such approach involved the use of a contour-enhanced funnel plot. The analysis of this plot revealed asymmetry, with a lack of studies on the left side of the funnel in both statistically non-significant and significant areas.

The absence of non-significant results in the bottom left region suggests the possibility of publication bias. Another contributing factor to the asymmetry is implied, given the scarcity of studies in the top-left section of the chart (Figure 4A). However, this asymmetry is less likely attributable to publication bias towards nonsignificant results, as the missing studies would fall into the area of high statistical significance.

Figure 4. Contour-enhanced funnel plot (A), centred at 0 (null hypothesis value) to aid interpretation, and (B) Trim and fill analysis funnel plot. The white and shaded sections represent areas of statistical non-significance and significance, respectively. For comparison, a standard funnel plot (C) is included.

Similar to the previously mentioned publication year effect, it is important to note that these results seem to support the notion that there might be a tendency to publish positive results over negative ones.

To complement the funnel plot analysis, a trim and fill test was employed to identify the location of missing studies on the chart and determine the quantity needed for symmetry. As expected, the analysis indicated the addition of six studies to the left side of the chart to achieve funnel plot symmetry (see Figure 4B). However, most of the filled studies were situated in the region of higher statistical significance, suggesting that the asymmetry may not only be attributed to publication bias (Peters et al., 2008). Alternative factors, such as location biases (especially language bias, as only studies in English were included in this analysis) or true heterogeneity (possibly due to differences in the intensity of the interventions), are plausible (Borenstein et al., 2009; Rothstein et al., 2005).

Lastly, we used a regression test designed to assess funnel plot asymmetry, commonly known as Egger’s test. Specifically, the random/mixed effects version, as recommended by Rothstein et al. (2005) and Viechtbauer (2010), was employed due to the model used for estimating the overall effect. This test aimed to quantify the potential association between effect sizes and standard error, which often serves as an indicator of funnel plot asymmetry. The obtained results were consistent with the trim-and-fill method, revealing a regression intercept with a p-value of 0.09 (t = 1.76). This finding suggests limited evidence supporting the presence of bias towards studies with statistically non-significant results. Hence, confirmation of publication bias could not be established.

3.5. Sensitivity analysis

Sensitivity analyses were performed in two stages: firstly, by including studies to achieve symmetry based on the results of the fill and trim, and secondly, by excluding effect size outliers. A summary of the sensitivity analyses is provided in Table S4 of Appendix S1.

As previously mentioned, the fill and trim test indicated the potential omission of six studies from the left side of the funnel plot. The overall effect decreased upon their inclusion, yet it remained positive and statistically significant (k = 50, logOR = 0.86, p < 0.0001).

In the second sensitivity analysis, the dmetar package was used to remove outliers, defined as studies whose 95% confidence interval extended beyond the 95% confidence interval of the combined effect (Harrer et al., 2019). This process resulted in the exclusion of 12 studies, considerably lowering the between-study heterogeneity (I ² = 61.35%). Despite this, the pooled effect continued to be moderately positive and statistically significant (k = 32, logOR = 1.10, p < 0.0001).

It is important to emphasise that this outcome highlights the robustness of the association between language learning and mathematical skills in young adolescents, despite the data suggesting the presence of publication bias.

4. Discussion

The objective of this study was to synthesise existing research on the impact of formal second language learning during early adolescence on mathematical skills. The 25 included studies in the systematic review exhibited considerable methodological diversity, especially evident in areas such as sample selection, number of participants, assessment tools used and the statistical methods employed.

This diversity resulted in a highly heterogeneous mix of effect sizes and confidence intervals. When meta-analysed, these yielded a medium-sized effect, according to the field-specific benchmark established by Plonsky et al. (2021). Specifically, students who underwent formal language learning, either participating in a BE program or a second/foreign language program, were three times more likely to achieve higher grades on a mathematical test compared to those without such exposure.

It is well known that meta-analytical results are contingent upon the reliability of the synthesised data. If the area of study has been subjected to any type of selection bias, such as publication bias, the results may be affected (Borenstein et al., 2009). In this study, both the moderating variables (specifically, year of publication) and funnel plot analyses suggest a tendency to favour the publication of positive results over negative ones and significant findings over non-significant ones. However, it is crucial to note that the results of the trim and fill analysis as well as Egger’s test indicate publication bias could not be confirmed.

Given the pronounced heterogeneity observed in the model, an in-depth exploration of potential factors influencing the overall result was conducted. Analyses addressing study clusters, filling in potentially missing studies (as a result of the trim and fill analysis) and excluding outliers consistently yielded positive and statistically significant effect sizes. These results revealed that students learning a second language were at least 1.84 times more likely to outperform their counterparts in control groups when assessed in a mathematical skills test. Although we recognise it is possible that future meta-analyses in this area may yield a different result, this data suggests that most studies analysing the impact of language learning on mathematical skills should be able to demonstrate a correlation of comparable magnitude to ours.

As numerous authors have recently stated, language learning and bilingualism are dynamic phenomena, existing along a continuum influenced by a myriad of factors (Beatty-Martínez & Titone, 2021; de Bruin, 2019; Gullifer et al., 2018; Titone & Tiv, 2023). In line with the ongoing debate regarding the cognitive benefits attributed to learning a second language, it is understood that such effects may be contingent upon said factors. Within the constraints of the data collected, several covariates were analysed, revealing SES and intervention duration as the most influential and statistically significant, contributing to 46% and 10% of the between-study heterogeneity, respectively. Specifically, higher SES levels and longer formal language training programs both correlated with higher test results.

The assertion that SES and the duration of the intervention affect student performance, and thus effect sizes, is substantiated by existing literature. Firstly, empirical evidence from international standardised tests reveals that, even among high-performing nations, SES significantly impacts test results. Specifically, lower socio-economic status, as measured by a composite of social, financial, cultural and human capital factors, correlates with diminished student performance (Mullis et al., 2020; OECD, 2019, 2023b). Moreover, research indicates that increased exposure and practice in a second language enhance the likelihood of attaining cognitive benefits derived from linguistic experiences (Bialystok, 2015). Consequently, our observation that longer interventions yield higher effect sizes aligns logically with this established framework.

Other factors documented in the literature as influential in shaping the bilingual experience, such as the type of language intervention/exposure – particularly full language immersion (Farabolini et al., 2023; Figueiredo et al., 2016) – and age, which generally favours learners under six years of age (Planckaert et al., 2023), were also analysed. However, these factors did not exhibit a statistically significant influence on our model and resultant effect size.

Regarding the lack of differential effect based on the type of language program, we believe this result is attributable to the nature of the data. That is, the majority of the effect sizes were based on samples that included students with an immigrant background participating in various types of bilingual and second language programs aimed at effectively introducing them to mainstream programs. An interpretation of this finding might be that when the intervention is a second language program designed as immigration aid (i.e., when the dominant language is the one being learnt), it provides the same level of exposure, in terms of understanding how the language works and how it can be used as an everyday communication tool, as bilingual programs. This similarity in exposure likely results in similar reported effect sizes.

Interestingly, the remaining programs, whose populations were learning languages that were not necessarily widely spoken in their geographical area, reported effect sizes that were mostly within the confidence intervals of the overall effect. This may suggest that under specific circumstances, a foreign language learning setting might provide benefits similar to those of full immersion. This could be particularly true when foreign language programs incorporate cultural and practical language components, ensuring comprehensive engagement and communication skills designed for immediate real-world application. Additionally, as foreign language learning is often optional, the learners’ high motivation may play an important role in their success.

The absence of a clear pattern between participants’ age at the time of testing and effect sizes – meaning that neither older nor younger students performed significantly better on mathematical tests – is somewhat unexpected. This, however, could be explained by the presence of other factors that influence cognitive ability at specific ages, such as gender, or by factors that may be more influential but were not recorded in the study, such as home language (dominancy, proficiency, etc.), cultural values and attitudes towards language learning or heritage language. Another interpretation of this finding is that within the age range studied, the age of testing is not a determining variable in the association between language learning and mathematical ability.

This meta-analysis is the first, to our knowledge, to aggregate studies examining the association between language learning and mathematical skills during early adolescence. While our findings are promising, it is imperative to acknowledge that causation cannot be definitively inferred. Our study does not establish whether students excel in mathematics due to participating in language courses, or if those proficient in mathematics are more inclined to opt for language courses. Notably, more than half of the effect sizes in our dataset were derived from populations where students were learning a second language as a migration aid. These individuals engaged in language learning not solely out of intrinsic motivation but due to a change in circumstances, which highlights the potential cognitive benefits of second language acquisition.

Additionally, existing research offers some support for the benefits of language learning on mathematical ability. Certain authors have identified a positive correlation between language learning and mathematical skills, albeit in younger age groups (Iqbal, 2022; Lin, 2018; Stewart, 2005; Tobias, 2012). Furthermore, the literature extensively documents the positive impact of language learning on non-linguistic cognitive skills (Poarch & van Hell, 2012; White & Greenfield, 2017; Woumans et al., 2018; Yurtsever et al., 2023), with mathematical achievement accurately predicted by these skills (Bellon et al., 2019; Cantin et al., 2016; Cragg et al., 2017).

This correlation is substantiated by international standardised tests data, as evidenced by consistently superior performance in the SAT mathematics section among students who engaged in language learning (CollegeBoard, 2019, 2020, 2021, 2022, 2023). Likewise, the ten highest-performing countries in mathematics in PISA 2022 are nations where more than 85% of students are at least learning one foreign language in their school settings (OECD, 2020, 2023b).

5. Limitations and future directions

Although this review adhered to rigorous guidelines and a robust searching strategy, it is important to acknowledge its limitations. Most included studies were conducted in North America, with only one exception in Asia, leaving other regions unrepresented. Greater geographical diversity would have been beneficial, given the significant global variation in attitudes towards foreign language learning (OECD, 2020, 2023a). This limitation can be partially attributed to the deliberate selection of English as the language criterion for the sourced studies. Future meta-analyses incorporating research in various language could enhance the geographical diversity and robustness of findings.

Furthermore, this review also identified substantial heterogeneity between studies, with mixed-effects modelling attributing some differences to variations in SES, the length of intervention and publication year. However, a significant residual heterogeneity persisted, suggesting the existence of unaccounted-for variables. Consequently, additional research is needed to systematically identify additional confounding factors, such as gender, thereby elucidating the nature of the association between language learning and mathematical skills.

Finally, it is important to note that due to the dynamic nature of cognitive skills and language learning, their interaction is inherently complex. Therefore, experimental research conducted under controlled settings is essential to establish causation. Rigorous methods such as matched-paired sample selection, homogenous interventions and time-lagged correlations, along with a thorough evaluation of the role of EF, may enhance the robustness and decisiveness of findings. Nevertheless, challenges remain in comparing bilingual populations, as their language learning experiences and cognitive realities may vary significantly across and within studies (Titone et al., 2024). This variability may complicate the ability to draw definitive conclusions about this fundamentally complex area of study.

6. Conclusion

This study synthesised research on the impact of formal second language learning during early adolescence on mathematical skills. The systematic review of 25 studies revealed significant methodological diversity, leading to heterogeneous effect sizes. The subsequent meta-analysis showed a medium-sized effect, indicating that students in bilingual or second language programs performed three times better on math tests than those without such exposure. Methodological diversity among studies, particularly in sample selection and statistical methods, was observed. However, sensitivity analyses confirmed the overall effect remained robust, with language learners outperforming their monolingual counterparts at least 1.84 times. SES and intervention duration were identified as influential factors affecting the outcomes.

Nevertheless, limitations included a geographic bias and residual heterogeneity in the data. Future research should address these limitations and investigate causation through experimental studies. Our findings emphasise the significance of language learning in educational policy and practice, suggesting a positive correlation between language learning and mathematical skills that warrants further exploration.