FFQ are commonly used to assess dietary intake in large epidemiological studies(Reference Thompson and Byers1). Despite comments on their validity, FFQ will continue to be used as they can be distributed in much larger populations than food records(Reference McNeill, Masson and Macdonald2) and are able to assess intake with a longer reference period than, for example, food records or 24 h recalls.
Basically, an FFQ consists of a food list enumerating the most informative food items for the purpose of a study. A food list should be as short as possible because long lists are less cost and time efficient, may bore respondents and make them less motivated to fill out an FFQ(Reference Willett3). Informative food items need to fulfil three general characteristics. The food must be consumed regularly, contribute substantially to the nutrient(s) of interest and be able to rank individuals according to their intake, i.e. varying in use between persons(Reference Willett3).
Willett(Reference Willett3) describes three different procedures to select informative food items. A simple procedure identifies food items with a high nutrient content from published food composition tables. However, this approach might lead to inclusion of food items that are consumed infrequently. The second procedure uses open-ended food intake data from a population, such as those obtained by food records or 24 h recalls. Food items are selected on the basis of their percentage contribution to nutrient intake in a population(Reference Block, Hartman and Dresser4). This selection procedure is simple and suitable if the purpose of the FFQ is to estimate the absolute level of intake in a population. A third approach, forward regression, uses similar data but predicts the food items that explain most variance, taking covariance between nutrient intakes of food items into account. This selection procedure is very suitable if the purpose of the FFQ is to rank or classify individuals according to their intake, e.g. in epidemiological studies.
It is essential that the food list of an FFQ is adapted to relevant new foods introduced on the food market, food patterns in the target population and to nutrients of interest(Reference Kristal, Feng and Coates5). For this reason, it is recommended to develop new FFQ for each study; however, as this process is highly labour-intensive, often existing ‘old’ questionnaires are reutilised or modified(Reference Subar6). To facilitate the development of tailor-made FFQ, the authors devised a new computer system in which food lists will be automatically generated and updated in a standardised way. For item selection, this computer system will use food consumption databases of the population of interest and food composition tables.
For this computer system, we needed a feasible approach to select relevant food items automatically from the databases. The second approach described by Willett, which includes food items highly contributing to the level of nutrient intake of the total population, could be incorporated relatively simply into our computer system. Incorporation of the third approach, described by Willett, using forward regression is much more complicated. Forward regression evaluates many different combinations of food items and their estimated regression coefficients in order to provide the combination that explains the highest variance in nutrient intake based on their variance and covariance. This process overloads the computer system, because large databases are used and regression analysis tests all possible combinations in search of the most optimal combination of food items. An alternative method simply selects food items based on variance in nutrient intake only. Since this method does not take covariance in nutrient intake of different food items and their estimated regression coefficients into account, and tests only one combination of food items(Reference Mark, Thomas and Decarli7), it does not overload the computer system. This procedure refers to the second moment (the variance) of the nutrient intake distribution and was therefore previously(Reference Mark, Thomas and Decarli7) called MOM2.
The aim of the present study was to compare food lists made by MOM2, which identifies food items explaining most of the variance in nutrient intake without taking other items into account, with food lists made by forward regression and to compare both procedures.
Methods
Data
Food consumption data of the Dutch National Food Consumption Survey of 1997/1998 were used for selecting food items. This dataset comprised 6250 non-institutionalised persons aged 1–97 years in 2564 households, representative of the Dutch population according to sociodemographic characteristics(8). For the present illustration of the method, we selected data of adults between 25 and 65 years of age, forming a subpopulation of 3524 adults.
Information on food consumption in this dataset was obtained with a 2 d food record, and the average intake on these two consecutive days was used. The foods consumed at home were recorded in a household diary for all individual members of the household by the person usually engaged in preparation of the meals. Consumption out of home was recorded by every participant in a personal diary. Food consumption data were collected during 40 weeks/year, and for the total population, these data were evenly distributed over the seasons and all days of the week.
Nutrient intake was calculated using the Dutch food composition table, NEVO 1996(9).
Choice of nutrients
In order to study the suitability of the selection procedures, various nutrients that represent different aspects of the food pattern were incorporated. We focused on carbohydrates and fat to represent the energy-yielding macronutrients. To these, we added vitamin C as a representative nutrient for vegetables, fruit and vitamins, dietary fibre for vegetables, fruit and cereals, and Ca for dairy foods and minerals.
Grouping of food items
Food items may be enquired at different aggregation levels depending on the level of detail required for the purpose of the study. Therefore, we divided foods into several subgroups at different levels of aggregation. Foods in the Dutch food composition table are combined into twenty-four food groups such as ‘bread’, ‘fruit’ and ‘vegetables’. These food groups comprise a large number of foods, and are not suitable for being used as items in an FFQ. Therefore, these twenty-four food groups, regarded as hierarchical level 1, were further subdivided into smaller food groups at four hierarchical levels of aggregation of food items. This was done by two dietitians based on similarity in eating occasions, portion sizes and nutrient contents. In total, 87, 237 and 356 food items were present at aggregation levels 2, 3 and 4, respectively. An illustration of this subdivision is given for dietary fibre in bread (Fig. 1).
Fig. 1 Example of aggregation levels for the food group ‘bread’.
Statistical methods
Selection of food items by MOM2
We selected food items using MOM2, i.e. a procedure that identifies food items starting with those that explain the largest variances in nutrient intake(Reference Mark, Thomas and Decarli7). This method does not take covariance in nutrient intake of different food items into account, and tests only one combination of food items. In order to select food items, individual nutrient scores were calculated for all food items. This score F ij is defined as the amount of nutrient consumed by individual i (i = 1,…, n) in food item j (j = 1,…, k) (2). Nutrient scores over k subsequently selected food items add up to W i, i.e. 
. For the selection process, foods are ranked on the basis of the variance in their nutrient score 
, with 
the mean nutrient score of food item j over all individuals. For the selection of food items, 
was computed, i.e. the ratio of the variance in nutrient intake in the selected subset of food items W i to the variance in the total nutrient intake Z i over all food items in the dataset i.e. 
(1). The selection of food items was stopped when it exceeded a preset criterion, i.e. 80 % of W i over Z i; thus:
In this formula, 
represents the mean nutrient intake for all individuals from selected food items and 
represents the mean nutrient intake for all individuals from all food items in the dataset.
Food items were selected per nutrient and for three different aggregation levels of food items separately. These were aggregation levels 2–4, and an illustration of this subdivision is given for dietary fibre in bread (Fig. 1). For an overview of selection procedures, see Table 1.
Table 1 Overview of selection procedures and evaluation criteria to select important food items for a FFQ that explain variance or contribute to nutrient intake of the total population
* MOM2 refers to variance or the second moment of the nutrient intake distribution.
† k is the number of selected food items; F ij is the nutrient score computed for individual i (i = 1,…, n) in a food item j (j = 1,…, k). 
is the mean nutrient score of a food item over all individuals.
‡ 
is the percentage of total variance covered, W i is the nutrient score computed for k selected food items for an individual i, 
is the mean nutrient score for k selected food items over all individuals Z i is the nutrient intake by all food items in the dataset for individual i, 
is the average nutrient score from all food items in the dataset over all individuals.
§ 
is the predicted nutrient intake for individual i; 
is the average predicted nutrient intake for all individuals n.
∥ 
is the explained variance calculated by regression; α0 is the intercept in regression formula, α1 is the regression coefficient that accompanies predicted nutrient score of a food item; ɛi is the error term in regression formula for individual i. Note that the error terms over all individuals sum to zero.
Selection of food items by forward regression analysis
Forward regression analysis was used as reference method to identify food items that explain most of the variance for each nutrient. Total nutrient intake (Z i) obtained by all food items for all individuals i (i = 1,…, n) in the dataset was regressed on nutrient score F ij. 
(Reference Rosner, Willett and Spiegelman10). Forward regression analysis adds food items to the selection starting with those with the highest predicted explained variance based on total nutrient intake and their estimated regression coefficients. This method does take covariance in nutrient intake of different food items into account, and tests all possible combinations of food items. The addition of food items stopped if the predicted variance based on the k selected food items exceeded 80 % of the total variance in Z i.
In which, 
represents the predicted nutrient intake for individual i and 
represents the mean predicted nutrient intake over all n individuals.
Evaluation of selected foods by MOM2
Food items selected by MOM2 were evaluated for each nutrient separately on the following three characteristics: differences in (1) types and (2) number of food items compared to selected food items by forward regression and (3) the percentage of explained variance by regression computed for food lists developed by MOM2 and entered in regression analysis. This was obtained by squaring the correlation between nutrient intake by food items on the food list of the FFQ and nutrient intake by the total dataset. This provides an estimate of explained variance(Reference Byers, Marshall and Fiedler11) and is easy to process because of the limited food list.
For comparison, we used the food items selected by MOM2 and forward regression to calculate the ‘percentage contribution’ to population intake(Reference Block, Hartman and Dresser4), see formula (3). This percentage contribution is important if the FFQ is meant to assess absolute intakes. Percentage contribution was computed by adding nutrient scores for the k selected food items 
. This was divided by the cumulative nutrient score for all food items, 
. Subsequently, percentage contribution to population intake was calculated as:
in which W i represents nutrient intake of subject i from a selected subset of k food items and Z i represents nutrient intake of subject i over all items in the dataset, i.e. the reference value for total nutrient intake.
Order of selections for different nutrients
We studied whether the order of selections for different nutrients influenced the final food list for different combinations of nutrients, because the nutrient for which food items were first selected can reach a much higher percentage of explained variance in the final food list than the required 80 %. New food items selected for the second and further nutrients were added to the list of foods selected for the first nutrient. In the first approach, the order was from the nutrient, of which 80 % variance was explained by the lowest number to the nutrient explained by the highest number of food items. In the alternative approach, the reverse order was used. To study these effects, food lists developed by MOM2 with food items defined at aggregation level 2 were used. Analyses were done for the following sets of nutrients: vitamin C and carbohydrates, fat and carbohydrates, and dietary fibre and carbohydrates. Finally, we compared the order of selections for all nutrients in the present study: vitamin C, Ca, fibre, total fat and carbohydrates.
All analyses were performed in Statistical Analysis System, version 9.1 (SAS Institute, Inc., Cary, NC, USA).
Results
Selection by the MOM2 procedure
Selection at aggregation level 2
For the five nutrients of interest, Table 2 shows the results for the three evaluation criteria, comparing the MOM2 procedure to the regression approach. An important result was that food items selected by MOM2, covering 80 % of variance 
, also covered at least 80 % of explained variance by regression analysis (Table 2). MOM2 selected one or two food items more for macronutrients than forward regression and the same number of items for dietary fibre, vitamin C and Ca. As an example, differences between the fifteen food items included by MOM2 and the thirteen food items included by forward regression for carbohydrates at aggregation level 2 were studied in more detail (Table 3). Eleven selected food items were identical for both procedures, though the order of their inclusion differed, whereas MOM2 included four food items that were not included by forward regression. Specifically, both procedures included ‘rice’, but MOM2 included ‘cooked potatoes’, ‘pasta’ and ‘ready-to-eat meals’, whereas forward regression did not. This is possibly due to the negative correlation between ‘cooked potatoes and ‘rice’ r = − 0·18, ‘pasta’ r = − 0·19 and ‘ready to eat meals’ r = − 0·14.
Table 2 Food items selected based on 80 % of variance in nutrient intake, MOM2, compared to selections that explain 80 % of variance by forward regression for carbohydrates, total fat, fibre, vitamin C and calcium evaluated for food items at three aggregation levels
MOM2, selects food items that explain variation in nutrient intake in a population.
Table 3 Food items selected to explain 80 % of MOM2 compared to selections by forward regression for carbohydrates at aggregation level 2
* Food items included by MOM2, but not by forward regression.
† Food items included by regression, but not by MOM2.
Food items selected by MOM2 also resulted in slightly higher percentages contribution to population intake (ranging from 57 % for vitamin C to 75 % for carbohydrates) than those by regression analysis (ranging from 57 % for vitamin C to 68 % for total fat and dietary fibre). In summary, MOM2 performed similarly to regression analysis, although MOM2 selected a few more food items than forward regression.
Selection at aggregation level 3
At aggregation level 3, food items selected by MOM2, covering 80 % of variance 
, reached 76 % of explained variance by regression analysis for carbohydrates to 84 % for vitamin C (Table 2). MOM2 selected twenty food items for carbohydrates, which was less than the twenty-four food items by forward regression. In contrast, MOM2 included twenty-eight food items for total fat compared to twenty-five food items by forward regression. Food items selected by MOM2 on aggregation level 3 contributed to a slightly higher percentage contribution of population intake (56 % for Ca to 68 % for carbohydrates) than those by forward regression (51 % for vitamin C to 68 % for carbohydrates).
Selection at aggregation level 4
At aggregation level 4, food items selected by MOM2, covering 80 % of variance 
, reached 75 % of explained variance by regression for carbohydrates to 82 % for total fat and vitamin C (Table 2). MOM2 included forty-two food items for total fat, five more than forward regression, reaching 82 % of explained variance by regression. In contrast to this, MOM2 included fewer food items for carbohydrates than forward regression, twenty-four food items instead of twenty-nine. Fig. 2 shows results for selection of food items at aggregation level 4. The number of food items included by MOM2 was slightly higher than by forward regression analysis to reach a similar level of explained variance by regression. Fig. 2 also shows that the MOM2 procedure was much more efficient at selecting food items that explained variance than the percentage contribution procedure. With the same number of selected food items, MOM2 covered even 20–30 % more explained variance for dietary fibre and vitamin C than percentage contribution. In addition, percentage contribution to total population intake was similar for food items selected by MOM2 (53 % for Ca and vitamin C to 67 % for carbohydrates) and forward regression (51 % for vitamin C to 70 % for carbohydrates).
Fig. 2 Explained variance by regression for forward regression (—–), MOM2 (–○–) and percentage contribution to population intake (MOM1; -----) by the number of included food items at aggregation level 4. (a) Carbohydrates, (b) total fat, (c) dietary fibre, (d) vitamin C and (e) Ca.
Order of selecting nutrients
Regarding the order of selections for different nutrients, the total number of food items selected by MOM2 differed by at most two food items (Table 4). When foods were first selected for vitamin C followed by carbohydrates, fourteen food items were selected, and when the order was reversed, sixteen items were selected. For the combination of vitamin C, Ca, fibre, total fat and carbohydrates, twenty-three food items were included, and twenty-two for the opposite order. The percentage of explained variance reached by regression analysis for both selections did not differ by more than 3 %. Selections made first for nutrients of interest explained by the lowest number of food items, followed by those explained by a high number of food items, led to lowest total number of food items at the highest level of explained variance.
Table 4 Effect of order selections for different nutrients on the number of selected food items, explained variance of the nutrients for two opposing orders
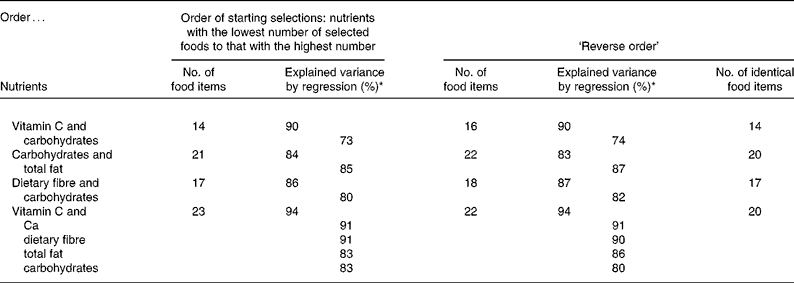
* Explained variance was calculated by regression analysis for all selected food items.
Discussion
For automated selection of informative food items for the food list of an FFQ, we evaluated a simple selection procedure, MOM2, which selects food items explaining the highest degree of variance in intake of selected nutrients. This simple approach was compared to food lists derived from forward regression that also takes covariance in nutrient intake into account. Food lists developed by MOM2 and forward regression were similar. Because MOM2 did not take covariance into account, it included a few more food items in order to reach a similar level of explained variance by regression. As a consequence, the percentage contribution to total population intake of the nutrients was slightly higher.
A novel aspect of the present study is that we evaluated MOM2 for the selection of food items for a food list of an FFQ using food consumption data collected with an open method, whereas previously MOM2 was used to shorten the food list of an existing FFQ(Reference Mark, Thomas and Decarli7). MAX_r, another selection procedure tested by the same authors, was not feasible to include in the present study, as it requires testing of all possible combinations of food items, even more than regression analysis that already overloaded the new computer system(Reference Thomas and Mark12). MOM2 was considered feasible and differences relative to regression depend on the dataset from which food items were selected. An important advantage of our dataset was that many different food items were included. An important limitation of the dataset used in the present study was that it was not optimal for regression analysis. Since only two subsequent food record days were available for each subject, between-person variance in this dataset was artificially high since this also contains part of day-to-day variation within persons(Reference Lambe, Kearney and Leclercq13). Also, the dataset included multiple persons from the same household, lowering between-person variance in food intake and increasing correlations between foods. With more recording days, the dataset would have better reflected the usual dietary pattern of individuals and would have been more suitable to select informative food items for an FFQ by regression analysis. Without covariances in food consumption, MOM2 and forward regression would have selected identical sets of food items(Reference Mark, Thomas and Decarli7). Although covariances between food items exist(Reference Mark, Thomas and Decarli7), variances (reflecting between-subject variance) for many food items are much larger than covariances, and therefore dominate the selection process resulting in comparable food lists by MOM2 and regression. This justifies the use of a much simpler method such as MOM2, which does not optimise the selection like forward regression.
To compare the performance of FFQ developed by MOM2 with those developed using other procedures, we included food lists developed by MOM2 in regression analysis and computed their explained variance. Explained variance, computed for food lists developed by MOM2, was only 0–5 % less than that for food lists developed by forward regression. The percentage contribution tended to be higher for MOM2 than for regression, especially at the most aggregated levels of food items, because food lists by MOM2 contained more food items due to the fact that covariances were not taken into account.
An advantage of automatically generating food lists is that this approach urges scientists to make the selection process and further decisions explicit, such as the grouping of food items. In the present study, we compared food lists by MOM2 and forward regression at different levels of aggregation. To develop an FFQ, food lists generated at different levels of aggregation need to be put together; for example, it has to be decided whether it is more informative to assess fibre intake by consumption of ‘bread’ than consumption of ‘whole wheat bread’, ‘white bread’, ‘croissants’ and ‘all other types of bread’ as separate items. Food items at a high aggregation level cover the percentage contribution of a nutrient better and result in a short list. This may result in a good list if the interest of the study is to assess the absolute level of intake of a population. However, in most studies, an FFQ is used to rank individuals according to their intake. Also, the tendency for assessment of dietary intake in future large epidemiological studies is to use several dietary assessment instruments in combination(Reference Subar, Dodd and Guenther14), and will often include a calibration study to an independent external standard(Reference Thompson, Kipnis and Midthune15). In these studies, FFQ are still needed to rank long-term intake of individuals, rather than the absolute level of intake. For this purpose, selecting food items at a detailed level is more suitable because it guarantees better capturing of the between-person variance in intake. However, a disadvantage of selecting food items at a detailed level is a longer food list. Currently, decisions of aggregating items are based on experience. Optimisation processes such as linear programming may help to decide on the most informative level of aggregation in future. However, a major limitation is that linear programming does not allow us to combine foods into new food groups during the process, for example, including ‘whole bread’ and create a new food group to assess ‘all other types of bread’. This new group may be important because all types of bread, which are on their own not relevant enough for assessing fibre intake, may be relevant in their combination. To find the optimal aggregation level for each nutrient, optimisation processes at lower levels must be ‘nested’ within higher aggregation levels, which requires algorithms beyond the scope of the present paper. Grouping of food items is often not explicitly described in literature, but, for future research, it would be important to automate this process and make it more transparent.
We focused on the statistical methods relevant to the selection of food items in an automated system; however, other factors are also important in developing FFQ. The way in which food items are grouped may also affect responses. For example, respondents may underestimate their food intake if fewer food items are included in the FFQ(Reference Serdula, Byers and Coates16), whereas increasing the number of items may lead to overreporting(Reference Bogers, Dagnelie and Westerterp17). The order in which food items are listed in the FFQ also influences responses(Reference Kuskowska Wolk, Holte and Ohlander18), for example, putting specific items in the FFQ before general items was shown to increase reported intake(Reference Cade, Thompson and Burley19). Moreover, it is important that a food list is comprehensible for respondents, and it may be desirable to add extra food items if this increases the face validity of FFQ. Modifications that increased comprehensibility improved validity of estimates of nutrient intake(Reference Thompson, Subar and Brown20). All these factors support that using a simpler method such as MOM2 is beneficial because the precision gained by using forward regression is limited compared with the impact of the above-mentioned factors. If the FFQ is meant to measure absolute intakes, percentage contribution is preferred.
A problem in generalising the present findings to developing food lists for complete FFQ may be that selection procedures were evaluated for only five nutrients. However, as they represent largely independent components of the habitual diet, we expect that these selection procedures behave similarly for other nutrients. We observed most differences for the macronutrients carbohydrates and fat, though these were minor regarding the number and type of items selected. For the micronutrients vitamin C and Ca, differences were very small, because a few indicator food items are sufficient to reflect variance in intake of these nutrients. For example, vitamin C intake is largely explained by fresh fruit, fruit juices and cooked or fried vegetables. It is even possible to extend MOM2 to selecting food groups such as vegetables, which are of increasing importance in public health. For this purpose, a new variable should be created for grams of vegetables so as to use variance in grams of vegetable intake for selecting the most discriminative types of vegetables. Another problem for generalising the present findings is that the order in which selections for different nutrients were made slightly affected the total number of food items included in the food list. When starting with the inclusion of foods for a specific nutrient, explained by a limited number of food items, foods added to explain further nutrients also add to explained variance for the earlier selected nutrients. We concluded from our analyses that the selection process is most efficient if it is started by selecting food items for nutrients that are explained by the smallest number of food items. To further evaluate the MOM2 selection procedure, we plan to develop an FFQ using MOM2 in order to select informative food items and validate this FFQ against another dietary assessment method and biomarkers of exposure.
Cultural differences are not considered to modify the present results importantly. The main differences in food consumption between countries in Europe are differences in the use of recipes, the number of different food items and the combination of foods consumed.
Regression analysis and MOM2 perform differently if there are very strong correlations between food items. In our dataset, we observed that French fries were strongly correlated to mayonnaise which is a typical Dutch combination. MOM2 selected both items, whereas regression analysis selected only one of them. This phenomenon only occurs if there is substantial covariance because of a very strong positive or negative association between food items, i.e. if they are almost always consumed in combination or the reverse, if they are almost never consumed in combination. The result of ignoring the covariance by using MOM2 is that MOM2 selects a few more food items than regression analysis and results in an FFQ that is (marginally) better able to catch variance in intake.
We conclude that for developing food lists for FFQ, it is not necessary to take covariance in nutrient intake into account; it appears sufficient to select food items based on the highest variance in nutrient intake.
Acknowledgements
The authors thank Saskia Meyboom and Henny Brants for their dietetic expertise in providing important background information for the development of the computer system such as grouping of food items at hierarchical aggregation levels. The present study was supported by the Netherlands Organization for Health Research and Development (ZonMw, grant 40-00 506-98-04-005). The authors declare that there are no conflicts of interest. M. L. M., J. H. M. d. V., N. D. and P. v. V. designed the study; M. L. M. and N. D. analysed the data; and M. L. M. wrote the manuscript. J. H. M. d. V. and P. v. V. revised earlier versions of the manuscript. J. H. M. d. V., M. C. O., P. C. D., R. A. G. and P. v. V. gave critical comments on the manuscript.
Appendix A SAS Codes
Percentage contribution (MOM1) procedure
*We imported a dataset that included food group names, all food codes, and nutrients contents. This file was sorted by food code and merged with the food consumption dataset;
*we kept only relevant variables;
libname Food ‘M:\selections\Food\’;
data Food.selMOM1;
set Food.selections;
*This example studies carbohydrates at aggregation level 2;
keep f2_group id amount carbohydrates_g;
run;
*These variables were labelled;
data Food.selMOM1;
set Food.selMOM1;
*The variable ‘amount’ is the amount of a specific food in grams consumed by one individual;
label amount = ‘amount’;
label id = ‘id’;
label f2_group = ‘Aggregation level 2’;
label carbohydrates_g = ‘carbohydrates per gram’;
run;
*We computed the total amount of carbohydrates per individual;
data Food.selMOM1;
set Food.selMOM1;
carbohydrates_total = amount*carbohydrates_g/100;
run;
*In this step we computed for each food item the total contribution to carbohydrate intake in the population;
ods output Summary = Food.MOM1;
proc means data = Food.selMOM1 sum;
class f2_group;
var carbohydrates_total;
run;
ods output close;
*In this step we computed the total amount of carbohydrates consumed from all food items;
ods output Summary = Food.MOM1tot;
proc means data = Food.selMOM1 sum;
var carbohydrates_total;
run;
ods output close;
data Food.MOM1;
set Food.MOM1;
label carbohydrates_total_sum = ‘total carbohydrates at level2’
run;
*In this step we added the variable type for merging the dataset;
data Food.MOM1;
set Food.MOM1;
rename carbohydrates_total_sum = carbohydratesgr2;
label carbohydratesgr2 = ‘carbohydrates at level2’;
_type_ = 0;
run;
data Food.MOM1tot;
set Food.MOM1tot;
type_ = 0;
run;
**In this step we merged the total amount of carbohydrates with the totals of carbohydrate per food item;
data Food.MOM1t;
merge Food.MOM1 Food.MOM1tot;
by type_;
run;
*We computed percentage contribution (MOM1) in the following step;
data Food.MOM1t;
set Food.MOM1t;
MOM1 = (carbohydratesgr2/carbohydrates_total_sum)*100;
drop _Type_ NObs;
run;
*This file was sorted by percentage contribution (MOM1)
proc sort data = Food.MOM1t;
by descending MOM1;
run;
*We included an export statement in SAS to save the data in Excel;
PROC EXPORT DATA = FOOD.MOM1T
OUTFILE = “M:\selections\Food\MOM1sortcarbo hydrates2.xls”
DBMS = EXCEL REPLACE;
SHEET = “MOM1 sorted carbohydrates2”;
RUN;
*End of computation of percentage contribution (MOM1);
***********************************************;
MOM2 procedure
*We computed the amount of carbohydrates that was consumed per person and per food item as in the MOM1 procedure;
libname Food ‘M:\selections\Food\’;
data Food.MOM2;
set Food.selections;
keep f2_group id amount carbohydrates_g;
run;
*We labelled these variables;
data Food.MOM2;
set Food.MOM2;
label amount = ‘amount’;
label id = ‘id’;
label f2_group = ‘Aggregation level 2’;
label carbohydrates_g = ‘carbohydrates per gram’;
run;
*We computed the total amount of carbohydrates per individual;
data Food.MOM2;
set Food.MOM2;
carbohydrates_total = amount*carbohydrates_g/100;
run;
ods output Summary = Food.sum;
proc means data = Food.MOM2 sum;
class id f2_group;
var carbohydrates_total;
run;
ods output close;
*We dropped the NObs variables (redundant);
data Food.sum;
set Food.sum;
drop nobs;
run;
*We labelled the total variable;
data Food.sum;
set Food.sum;
label carbohydrates_total = ‘Total amount of carbohydrates per food item at level 2’;
run;
*We transposed the data so that one individual had one row;
proc transpose data = Food.sum out = Food.transposed;
var carbohydrates_total_sum;
id f2_group;
by id;
run;
*We recoded all the missing values into zero consumption. Note that most missing values in our study are caused by missing values for micronutrients in the food composition table. They usually concern food items that are expected to be low in these nutrients;
data Food.transposed;
set Food.transposed;
array dffood{total number of food items}
_Bread _cookies _driedfruit _freshfruit _frenchfries _ice cream__potatoes _softdrinks etc. (list all food items);
do i = 1 to end;
if dffood{i} = . then dffood{i} = 0;
end;
run;
*We dropped redundant variables;
data Food.transposed;
set Food.transposed;
drop _NAME_ i;
run;
*We computed the y variable;
data Food.transposed_ycarbohydrates2;
set Food.transposed;
sum_carbohydrates = _Bread +_cookies +_dreadfruit + _freshfruit+_frenchfries +_icecream+_potatoes + _softdrinks etc. (list all food items);
+ potatoes+ etc.;
run;
* We computed the standard error of each group;
ods output Summary = Food.MOM2;
proc means data = Food.transposed_ycarbohydrates2 std;
var
_Bread _cookies _driedfruit _freshfruit _frenchfries _ice cream__potatoes _softdrinks etc. (list all food items);
run;
ods output close;
*Transpose to get the standard error of each group as a column;
proc transpose data = Food.MOM2 out = Food.MOM2t;
run;
*Drop the redundant _Label_ variable and calculate the variance of each group;
data Food.MOM2t;
set Food.MOM2t;
drop _LABEL_;
*COL1 is the standard error, which is squared to get the variance;
var = COL1*COL1;
label var = ‘Variance’;
drop COL1;
run;
*Calculate the percentage of total variance and sort the data;
proc means data = Food.MOM2t;
output out = Food.MOM2sum sum = MOM2sum;
run;
data Food.MOM2t;
set Food.MOM2t;
_type_ = 0;
run;
data Food.MOM2t;
merge Food.MOM2t Food.MOM2sum;
by _TYPE_;
run;
data Food.MOM2t;
set Food.MOM2t;
drop _Type_ _FREQ_;
MOM2 = var/MOM2sum*100;
drop var MOM2sum;
run;
proc sort data = Food.MOM2t out = Food.MOM2sorted carbohydrates2;
by descending MOM2;
run;
data Food.MOM2sortedcarbohydrates2;
set Food.MOM2sortedcarbohydrates2;
rename _name_ = name;
run;
*Computed MOM2 values are saved in an Excel file on disk M;
PROC EXPORT DATA = FOOD.MOM2SORTED CARBOHYDRATES2
OUTFILE = “M:\selections\Food\MOM2so rtcarbohydrates2.xls”
DBMS = EXCEL REPLACE;
SHEET = “MOM2sortcarbohydrates2”;
RUN;
***********************************************;
Regression analysis
*for regression analysis the above created file ‘Food. transposed_ycarbohydrates2’ was used;
proc reg data = Food.transposed_ycarbohydrates2 rsquare;
model sum_CARBOHYDRATES =
_Bread
_cookies
_driedfruit
_freshfruit
_frenchfries
_icecream
_potatoes
_softdrinks
etc. (list all food items);
/selection = forward details = summary;
run;
quit;
