Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-31T06:54:00.483Z Has data issue: false hasContentIssue false
  • English
  • Français

EXTENDED FRAMES AND SEPARATIONS OF LOGICAL PRINCIPLES

Part of: Model theory General logic Proof theory and constructive mathematics

Published online by Cambridge University Press:  26 July 2023

MAKOTO FUJIWARA Open the ORCID record for MAKOTO FUJIWARA [Opens in a new window] ,
HAJIME ISHIHARA ,
TAKAKO NEMOTO ,
NOBU-YUKI SUZUKI  and
KEITA YOKOYAMA Open the ORCID record for KEITA YOKOYAMA [Opens in a new window]
MAKOTO FUJIWARA
Affiliation:
DEPARTMENT OF APPLIED MATHEMATICS FACULTY OF SCIENCE DIVISION I, TOKYO UNIVERSITY OF SCIENCE 1-3 KAGURAZAKA, SHINJUKU-KU TOKYO 162-8601, JAPAN E-mail: makotofujiwara@rs.tus.ac.jp
HAJIME ISHIHARA
Affiliation:
SCHOOL OF INFORMATION SCIENCE JAPAN ADVANCED INSTITUTE OF SCIENCE AND TECHNOLOGY 1-1 ASAHIDAI, NOMI ISHIKAWA 923-1292, JAPAN E-mail: ishihara@jaist.ac.jp
TAKAKO NEMOTO
Affiliation:
GRADUATE SCHOOL OF INFORMATION SCIENCES TOHOKU UNIVERSITY 6-3-09 AOBA, ARAMAKI-AZA AOBA-KU SENDAI 980-8579, JAPAN E-mail: nemototakako@gmail.com
NOBU-YUKI SUZUKI
Affiliation:
DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE, SHIZUOKA UNIVERSITY OHYA 836, SURUGA-KU SHIZUOKA 422-8529, JAPAN E-mail: suzuki.nobuyuki@shizuoka.ac.jp
KEITA YOKOYAMA
Affiliation:
MATHEMATICAL INSTITUTE TOHOKU UNIVERSITY 6-3 ARAMAKI AZA-AOBA, AOBA-KU SENDAI 980-8578, JAPAN E-mail: keita.yokoyama.c2@tohoku.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We aim at developing a systematic method of separating omniscience principles by constructing Kripke models for intuitionistic predicate logic 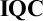$\mathbf {IQC}$ and first-order arithmetic 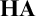$\mathbf {HA}$ from a Kripke model for intuitionistic propositional logic 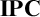$\mathbf {IPC}$. To this end, we introduce the notion of an extended frame, and show that each IPC-Kripke model generates an extended frame. By using the extended frame generated by an IPC-Kripke model, we give a separation theorem of a schema from a set of schemata in 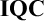$\mathbf {IQC}$ and a separation theorem of a sentence from a set of schemata in 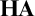$\mathbf {HA}$. We see several examples which give us separations among omniscience principles.

Keywords

extended frameKripke modellogical principle

MSC classification

Primary: 03F50: Metamathematics of constructive systems 03B55: Intermediate logics 03C30: Other model constructions

Information

Type
Articles
Information
Bulletin of Symbolic Logic , Volume 29 , Issue 3 , September 2023 , pp. 311 - 353
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Akama, Y., Berardi, S., Hayashi, S., and Kohlenbach, U., An arithmetical hierarchy of the law of excluded middle and related principles , Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science (LICS 2004) (Ganzinger, H., editor), IEEE Computer Society Press, Washington, DC, 2004, pp. 192–201.CrossRefGoogle Scholar
Ardeshir, M. and Mojtahedi, S. M., The de Jongh property for basic arithmetic . Archive for Mathematical Logic , vol. 53 (2014), nos. 7–8, pp. 881–895.CrossRefGoogle Scholar
Bishop, E., Foundations of Constructive Analysis , McGraw-Hill Book, New York–Toronto–London, 1967.Google Scholar
Bishop, E. and Bridges, D., Constructive Analysis, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 279, Springer, Berlin, 1985.CrossRefGoogle Scholar
Bridges, D. and Richman, F., Varieties of Constructive Mathematics , London Mathematical Society Lecture Note Series, vol. 97, Cambridge University Press, Cambridge, 1987.CrossRefGoogle Scholar
van Dalen, D., Logic and Structure , fifth ed., Universitext, Springer, London, 2013.CrossRefGoogle Scholar
Bridges, D. S. and Vîţă, L. S., Techniques of Constructive Analysis , Universitext, Springer, New York, 2006.Google Scholar
Fujiwara, M., ${\varDelta}_1^0$ variants of the law of excluded middle and related principles . Archive for Mathematical Logic , vol. 61 (2022), nos. 7–8, pp. 1113–1127.CrossRefGoogle Scholar
Fujiwara, M., Ishihara, H., and Nemoto, T., Some principles weaker than Markov’s principle . Archive for Mathematical Logic , vol. 54 (2015), nos. 7–8, pp. 861–870.CrossRefGoogle Scholar
Fujiwara, M. and Kohlenbach, U., Interrelation between weak fragments of double negation shift and related principles . The Journal of Symbolic Logic , vol. 83 (2018), no. 3, pp. 991–1012.CrossRefGoogle Scholar
Fujiwara, M. and Kurahashi, T., Refining the arithmetical hierarchy of classical principles . Mathematical Logic Quarterly , vol. 68 (2022), no. 3, pp. 318–345.CrossRefGoogle Scholar
Gabbay, D. M. and De Jongh, D. H. J., A sequence of decidable finitely axiomatizable intermediate logics with the disjunction property . The Journal of Symbolic Logic , vol. 39 (1974), pp. 67–78.CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic , Perspectives in Mathematical Logic, Springer, Berlin, 1993.CrossRefGoogle Scholar
Hosoi, T., On intermediate logics. I . Journal of the Faculty of Science, University of Tokyo, Section I , vol. 14 (1967), pp. 293–312.Google Scholar
Hosoi, T. and Ono, H., The intermediate logics on the second slice . Journal of the Faculty of Science, University of Tokyo, Section IA, Mathematics , vol. 17 (1970), pp. 457–461.Google Scholar
Ishihara, H., Continuity properties in constructive mathematics . The Journal of Symbolic Logic , vol. 57 (1992), no. 2, pp. 557–565.CrossRefGoogle Scholar
Ishihara, H., Markov’s principle, Church’s thesis and Lindelöf’s theorem . Indagationes Mathematicae. New Series , vol. 4 (1993), no. 3, pp. 321–325.CrossRefGoogle Scholar
Ishihara, H., Constructive reverse mathematics: Compactness properties , From Sets and Types to Topology and Analysis , Oxford Logic Guides, vol. 48, Oxford University Press, Oxford, 2005, pp. 245–267.CrossRefGoogle Scholar
Ishihara, H. and Nemoto, T., A note on the independence of premiss rule , Mathematical Logic Quarterly, vol. 62 (2016), nos. 1–2, pp. 72–76.CrossRefGoogle Scholar
Ishihara, H. and Nemoto, T., On the independence of premiss axiom and rule . Archive for Mathematical Logic , vol. 59, (2020), pp. 793–815.CrossRefGoogle Scholar
de Jongh, D., Verbrugge, R., and Visser, A., Intermediate logics and the de Jongh property . Archive for Mathematical Logic , vol. 50 (2011), nos. 1–2, pp. 197–213.CrossRefGoogle Scholar
Kaye, R., Models of Peano Arithmetic , Oxford Logic Guides, vol. 15, The Clarendon Press and Oxford University Press, New York, 1991.Google Scholar
Kohlenbach, U., On weak Markov’s principle. Mathematical Logic Quarterly , vol. 48, 2002, pp. 59–65, Dagstuhl Seminar on Computability and Complexity in Analysis, 2001.3.0.CO;2-I>CrossRefGoogle Scholar
Kohlenbach, U., Applied Proof Theory: Proof Interpretations and Their Use in Mathematics , Springer Monographs in Mathematics, Springer, Berlin, 2008.Google Scholar
Kohlenbach, U., On the disjunctive Markov principle , Studia Logica , vol. 103 (2015), no. 6, pp. 1313–1317.CrossRefGoogle Scholar
Leivant, D., Syntactic translations and provably recursive functions . The Journal of Symbolic Logic , vol. 50 (1985), no. 3, pp. 682–688.CrossRefGoogle Scholar
Lindström, P., Aspects of Incompleteness , second ed., Lecture Notes in Logic, vol. 10, Association for Symbolic Logic, Urbana; A. K. Peters, Natick, 2003.Google Scholar
Mandelkern, M., Constructively complete finite sets . Mathematical Logic Quarterly , vol. 34 (1988), no. 2, pp. 97–103.CrossRefGoogle Scholar
Ono, H., Kripke models and intermediate logics . Publications of the Research Institute for Mathematical Sciences , vol. 6 (1970/71), pp. 461–476.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , Perspectives in Mathematical Logic, Springer, Berlin, 1999.CrossRefGoogle Scholar
Smoryński, C., Lectures on nonstandard models of arithmetic , Logic Colloquium ’82 (Florence, 1982) , Studies in Logic and the Foundations of Mathematics, vol. 112, North-Holland, Amsterdam, 1984, pp. 1–70.Google Scholar
Smoryński, C. A., Applications of Kripke models , Metamathematical Investigation of Intuitionistic Arithmetic and Analysis , Lecture Notes in Mathematics, vol. 344, Springer, Berlin–Heidelberg, 1973, pp. 324–391.CrossRefGoogle Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics: An Introduction , vol. I, Studies in Logic and the Foundations of Mathematics, vol. 121, North-Holland, Amsterdam, 1988.Google Scholar
Veldman, W., Brouwer’s fan theorem as an axiom and as a contrast to Kleene’s alternative . Archive for Mathematical Logic , vol. 53 (2014), nos. 5–6, pp. 621–693.CrossRefGoogle Scholar
Visser, A., Substitutions of ${\varSigma}_1^0$ sentences: Explorations between intuitionistic propositional logic and intuitionistic arithmetic . Annals of Pure and Applied Logic , vol. 114 (2002), nos. 1–3, pp. 227–271, Commemorative Symposium Dedicated to Anne S. Troelstra (Noordwijkerhout, 1999).CrossRefGoogle Scholar
Wong, T. L., Lecture 4: The arithmetized completeness theorem. Lecture notes on model theory of arithmetic, 2014. Available at https://blog.nus.edu.sg/matwong/teach/modelarith/.Google Scholar