Article contents
Geometry, Calculus and Zil'ber's Conjecture
Published online by Cambridge University Press: 15 January 2014
Extract
§1. Introduction. By and large, definitions of a differentiable structure on a set involve two ingredients, topology and algebra. However, in some cases, partial information on one or both of these is sufficient. A very simple example is that of the field ℝ (or any real closed field) where algebra alone determines the ordering and hence the topology of the field:
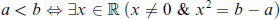
In the case of the field ℂ, the algebraic structure is insufficient to determine the Euclidean topology; another topology, Zariski, is associated with the ield but this will be too coarse to give a diferentiable structure.
A celebrated example of how partial algebraic and topological data (G a locally euclidean group) determines a differentiable structure (G is a Lie group) is Hilbert's 5th problem and its solution by Montgomery-Zippin and Gleason.
The main result which we discuss here (see [13] for the full version) is of a similar flavor: we recover an algebraic and later differentiable structure from a topological data. We begin with a linearly ordered set ⟨M, <⟩, equipped with the order topology, and its cartesian products with the product topologies. We then consider the collection of definable subsets of Mn , n = 1, 2, …, in some first order expansion ℳ of ⟨M, <⟩.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 4
- Cited by

