Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T13:59:04.242Z Has data issue: false hasContentIssue false
  • English
  • Français

AN APPLICATION OF RECURSION THEORY TO ANALYSIS

Part of: Set theory Classical measure theory Connections with other structures, applications Computability and recursion theory

Published online by Cambridge University Press:  11 June 2020

LIANG YU
LIANG YU*
Affiliation:
DEPARTMENT OF MATHEMATICS NANJING UNIVERSITY NANJING 210093, P.R. CHINA E-mail: yuliang.nju@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Mauldin [15] proved that there is an analytic set, which cannot be represented by $B\cup X$ for some Borel set B and a subset X of a 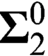$\boldsymbol{\Sigma }^0_2$ -null set, answering a question by Johnson [10]. We reprove Mauldin’s answer by a recursion-theoretical method. We also give a characterization of the Borel generated $\sigma $ -ideals having approximation property under the assumption that every real is constructible, answering Mauldin’s question raised in [15].

Keywords

hyperarithmeticanalytic setsKurtz-randomnessσ-idea

MSC classification

Primary: 03D30: Other degrees and reducibilities
Secondary: 03D32: Algorithmic randomness and dimension 03D80: Applications of computability and recursion theory 03E15: Descriptive set theory 28A05: Classes of sets (Borel fields, $sigma$-rings, etc.), measurable sets, Suslin sets, analytic sets 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 26 , Issue 1 , March 2020 , pp. 15 - 25
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Balcerzak, M., Can ideals without ccc be interesting? Topology and its Applications , vol. 55 (1994), no. 3, pp. 251–260.CrossRefGoogle Scholar
Boolos, G. and Putnam, H., Degrees of unsolvability of constructible sets of integers . Journal of Symbolic Logic , vol. 33 (1968), pp. 497–513.CrossRefGoogle Scholar
Chong, C. T. and Yu, L., Recursion Theory, De Gruyter Series in Logic and its Applications, vol. 8, De Gruyter, Berlin, 2015.CrossRefGoogle Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic randomness and complexity , Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Feferman, S., Some applications of the notions of forcing and generic sets . Fundamenta Mathematicae , vol. 56 (1964/1965), pp. 325–345.CrossRefGoogle Scholar
Franklin, J. N. Y. and Stephan, F., Van Lambalgen’s theorem and high degrees . Notre Dame Journal of Formal Logic , vol. 52 (2011), no. 2, pp. 173–185.CrossRefGoogle Scholar
Gandy, R. O., Proof of Mostowski’s conjecture . Bulletin L’Académie Polonaise des Science, Série des Sciences Mathématiques, Astronomiques et Physiques , vol. 8 (1960), pp. 571–575.Google Scholar
Guaspari, D., A note on the Kondo-Addison theorem . Journal of Symbolic Logic , vol. 39 (1974), pp. 567–570.CrossRefGoogle Scholar
Jensen, R. B., The fine structure of the constructible hierarchy . Annals of Mathematical Logic , vol. 4 (1972), pp. 229–308; erratum, ibid. 4 (1972), 443, 1972.CrossRefGoogle Scholar
Johnson, K. G., The $\sigma$ -algebra generated by the Jordan sets in ${R}^n$ . Real Analysis Exchange , vol. 19 (1993/1994), no. 1, pp. 278–282.CrossRefGoogle Scholar
Kechris, A. S. and Solecki, S., Approximation of analytic by Borel sets and definable countable chain conditions . Israel Journal of Mathematics , vol. 89 (1995), no. 1–3, pp. 343–356.CrossRefGoogle Scholar
Kjos-Hanssen, B., Nies, A., Stephan, F., and Yu, L., Higher Kurtz randomness . Annals of Pure and Applied Logic , vol. 161 (2010), no. 10, pp. 1280–1290.CrossRefGoogle Scholar
Kleene, S. C., Hierarchies of number-theoretic predicates . Bulletin of the American Mathematical Society , vol. 61 (1955), pp. 193–213.CrossRefGoogle Scholar
Martin, D. A., Proof of a conjecture of Friedman . Proceedings of the American Mathematical Society , vol. 55 (1976), no. 1, pp. 129.CrossRefGoogle Scholar
Mauldin, R. D., Analytic non-Borel sets modulo null sets , Set Theory (T. Bartoszyński and M. Scheepers, editors), Contemporary Mathematics, vol. 192, American Mathematical Society, Providence, RI, 1996, pp. 69–70.CrossRefGoogle Scholar
Miller, A. W., Some interesting problems, 2015. https://www.math.wisc.edu/miller/res/problems.pdf Google Scholar
Nies, A., Computability and Randomness , Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
Sacks, G. E., Higher recursion theory , Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.Google Scholar
Spector, C., Hyperarithmetical quantifiers . Fundamenta Mathematicae , vol. 48 (1959/1960), pp. 313–320.CrossRefGoogle Scholar
Suslin, M., Sur une definition des ensembles measurables b sans nombres transinis . Comptes Rendus de l’Académie des Sciences , vol. 164 (1917), pp. 88–91.Google Scholar
Yu, L., A new proof of Friedman’s conjecture, this Journal, vol. 17 (2011), no. 3, pp. 455–461.Google Scholar