Article contents
CATEGORICAL QUANTIFICATION
Published online by Cambridge University Press: 24 January 2024
Abstract
Due to Gödel’s incompleteness results, the categoricity of a sufficiently rich mathematical theory and the semantic completeness of its underlying logic are two mutually exclusive ideals. For first- and second-order logics we obtain one of them with the cost of losing the other. In addition, in both these logics the rules of deduction for their quantifiers are non-categorical. In this paper I examine two recent arguments—Warren [43] and Murzi and Topey [30]—for the idea that the natural deduction rules for the first-order universal quantifier are categorical, i.e., they uniquely determine its semantic intended meaning. Both of them make use of McGee’s open-endedness requirement and the second one uses in addition Garson’s [19] local models for defining the validity of these rules. I argue that the success of both these arguments is relative to their semantic or infinitary assumptions, which could be easily discharged if the introduction rule for the universal quantifier is taken to be an infinitary rule, i.e., non-compact. Consequently, I reconsider the use of the 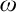 $\omega $-rule and I show that the addition of the
$\omega $-rule and I show that the addition of the 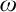 $\omega $-rule to the standard formalizations of first-order logic is categorical. In addition, I argue that the open-endedness requirement does not make the first-order Peano Arithmetic categorical and I advance an argument for its categoricity based on the inferential conservativity requirement.
$\omega $-rule to the standard formalizations of first-order logic is categorical. In addition, I argue that the open-endedness requirement does not make the first-order Peano Arithmetic categorical and I advance an argument for its categoricity based on the inferential conservativity requirement.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 3
- Cited by


