Forcing theory and combinatorics of the real line

Abstract

The main purpose of this dissertation is to apply and develop new forcing techniques to obtain models where several cardinal characteristics are pairwise different as well as force many (even more, continuum many) different values of cardinal characteristics that are parametrized by reals. In particular, we look at cardinal characteristics associated with strong measure zero, Yorioka ideals, and localization and anti-localization cardinals.

In this thesis we introduce the property “F-linked” of subsets of posets for a given free filter F on the natural numbers, and define the properties “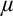$\mu $-F-linked” and “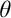$\theta $-F-Knaster” for posets in a natural way. We show that 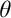$\theta $-F-Knaster posets preserve strong types of unbounded families and of maximal almost disjoint families. These kinds of posets led to the development of a general technique to construct 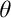$\theta $-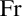$\textrm {Fr}$-Knaster posets (where 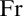$\textrm {Fr}$ is the Frechet ideal) via matrix iterations of 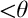${<}\theta $-ultrafilter-linked posets (restricted to some level of the matrix). The latter technique allows proving consistency results about Cichoń’s diagram (without using large cardinals) and to prove the consistency of the fact that, for each Yorioka ideal, the four cardinal characteristics associated with it are pairwise different. Another important application is to show that three strongly compact cardinals are enough to force that Cichoń’s diagram can be separated into 10 different values. Later on, it was shown by Goldstern, Kellner, Mejía, and Shelah that no large cardinals are needed for Cichoń’s maximum (J. Eur. Math. Soc. 24 (2022), no. 11, p. 3951–3967).

On the other hand, we deal with certain types of tree forcings including Sacks forcing, and show that these increase the covering of the strong measure zero ideal 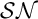$\mathcal {SN}$. As a consequence, in Sacks model, such covering number is equal to the size of the continuum, which indicates that this covering number is consistently larger than any other classical cardinal characteristics of the continuum. Even more, Sacks forcing can be used to force that 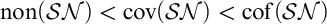$\operatorname {\mathrm{non}}(\mathcal {SN})<\operatorname {\mathrm{cov}}(\mathcal {SN})<\operatorname {\mathrm{cof}}(\mathcal {SN})$, which is the first consistency result where more than two cardinal characteristics associated with $\mathcal {SN}$ are pairwise different. To obtain another result in this direction, we provide bounds for $\operatorname {\mathrm{cof}}(\mathcal {SN})$, which generalizes Yorioka’s characterization of $\mathcal {SN}$ (J. Symbolic Logic 67.4 (2002), p. 1373–1384). As a consequence, we get the consistency of 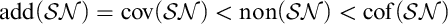$\operatorname {\mathrm{add}}(\mathcal {SN})=\operatorname {\mathrm{cov}}(\mathcal {SN})<\operatorname {\mathrm{non}}(\mathcal {SN})<\operatorname {\mathrm{cof}}(\mathcal {SN})$ with ZFC (via a matrix iteration forcing construction).

We conclude this thesis by combining creature forcing approaches by Kellner and Shelah (Arch. Math. Logic 51.1–2 (2012), p. 49–70) and by Fischer, Goldstern, Kellner, and Shelah (Arch. Math. Logic 56.7–8 (2017), p. 1045–1103) to show that, under CH, there is a proper 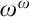$\omega ^\omega $-bounding poset with 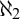$\aleph _2$-cc that forces continuum many pairwise different cardinal characteristics, parametrized by reals, for each one of the following six types: uniformity and covering numbers of Yorioka ideals as well as both kinds of localization and anti-localization cardinals, respectively. This answers several open questions from Klausner and Mejía (Arch. Math. Logic 61 (2022), pp. 653–683).

Abstract prepared by Miguel Antonio Cardona-Montoya

E-mail: miguel.cardona@upjs.sk

URL: https://repositum.tuwien.at/handle/20.500.12708/19629