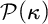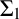This thesis is divided into three parts, the first and second ones focused on combinatorics and classification problems on discrete and geometrical objects in the context of descriptive set theory, and the third one on generalized descriptive set theory at singular cardinals of countable cofinality.
Descriptive Set Theory (briefly: DST) is the study of definable subsets of Polish spaces, i.e., separable completely metrizable spaces. One of the major branches of DST is Borel reducibility, successfully used in the last 30 years to solve and compare many classification problems. One of our goals is the classification of knots, very familiar and tangible objects in everyday life, which also play an important role in modern mathematics. The study of knots and their properties is known as knot theory. Our plan is to gain insight into knots using discrete objects, such as linear and circular orders. This approach was already exploited in [6]. The first part of this work is therefore devoted to countable linear orders and the study of the quasi-order of convex embeddability and its induced equivalence relation. We obtain both combinatorial and descriptive set-theoretic results. We also expand our research to the case of circular orders.
Another objective of this first part is to extend the notion of convex embeddability on countable linear orders. We provide a family of quasi-orders of which embeddability is a particular case as well. We study these quasi-orders from a combinatorial point of view and analyse their complexity with respect to Borel reducibility. Furthermore, we extend the analysis of these quasi-orders to the set of uncountable linear orders.
The second part of the project deals with classification problems on knots and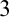 
$3$-manifolds. The goal here is to apply the results obtained in the first part to the study of proper arcs and knots, establishing lower bounds for the complexity of some natural relations between these geometrical objects. We also obtain some combinatorial results which are particularly interesting when we restrict to the set of wild proper arcs and wild knots, classes which haven’t received much attention so far. These parts are included in the two preprints [4, 5] in collaboration with my supervisor Alberto Marcone, Luca Motto Ros (University of Torino), and Vadim Weinstein (University of Oulu).
The second part of this work also includes the classification of non-compact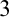 
$3$-manifolds up to homeomorphism (the case of compact 
$3$-manifolds has already been solved: indeed, there are only countably many 
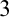$3$-manifolds up to homeomorphism; see [7]), and that of Cantor sets of 
$\mathbb {R}^3$ up to conjugation (answering to Question 5.5 of [3]). Here we resort to algebraic tools. Stone duality gives a neat way to go back-and-forth between totally disconnected Polish spaces and countable Boolean algebras (see [1]). The main ingredient is the Stone space of all ultrafilters on a Boolean algebra. In this work we introduce a weaker concept which we call “blurry filter”. Using blurry filters instead of ultrafilters enables one to extend the class of spaces under consideration beyond totally disconnected. As an application of this method, we show that both homeomorphism on non-compact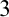 
$3$-manifolds and conjugation of Cantor sets in 
$\mathbb {R}^3$ are completely classifiable by countable structures. These results are part of an upcoming paper in collaboration with Vadim Weinstein.
The last part of this thesis concerns the natural generalization of descriptive set theory that occurs when countable is replaced by uncountable, called Generalized Descriptive Set Theory (briefly: GDST). In particular, we focus on the case of GDST for a singular cardinal 
$\kappa $ of countable cofinality. The goal here is to study the generalizations of the Perfect Set Property and the Baire Property to subsets of spaces of higher cardinalities, like the power set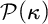 
$\mathcal {P}(\kappa )$. We consider the question under which large cardinal hypotheses classes of definable subsets of these spaces possess such regularity properties, focusing on rank-into-rank axioms, like I2, and classes of sets definable by 
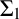$\Sigma _1$-formulas with parameters from various collections of sets. The obtained results are included in [2], a joint work with my co-supervisor Vincenzo Dimonte and Philipp Lücke (University of Hamburg).
Abstract prepared by Martina Iannella
E-mail: martina.iannella@tuwien.ac.at.
URL: https://air.uniud.it/handle/11390/1262824.
