Article contents
The Mathematical Import of Zermelo's Well-Ordering Theorem
Published online by Cambridge University Press: 15 January 2014
Extract
Set theory, it has been contended, developed from its beginnings through a progression of mathematical moves, despite being intertwined with pronounced metaphysical attitudes and exaggerated foundational claims that have been held on its behalf. In this paper, the seminal results of set theory are woven together in terms of a unifying mathematical motif, one whose transmutations serve to illuminate the historical development of the subject. The motif is foreshadowed in Cantor's diagonal proof, and emerges in the interstices of the inclusion vs. membership distinction, a distinction only clarified at the turn of this century, remarkable though this may seem. Russell runs with this distinction, but is quickly caught on the horns of his well-known paradox, an early expression of our motif. The motif becomes fully manifest through the study of functions 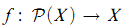 of the power set of a set into the set in the fundamental work of Zermelo on set theory. His first proof in 1904 of his Well-Ordering Theoremis a central articulation containing much of what would become familiar in the subsequent development of set theory. Afterwards, the motif is cast by Kuratowski as a fixed point theorem, one subsequently abstracted to partial orders by Bourbaki in connection with Zorn's Lemma. Migrating beyond set theory, that generalization becomes cited as the strongest of fixed point theorems useful in computer science.
of the power set of a set into the set in the fundamental work of Zermelo on set theory. His first proof in 1904 of his Well-Ordering Theoremis a central articulation containing much of what would become familiar in the subsequent development of set theory. Afterwards, the motif is cast by Kuratowski as a fixed point theorem, one subsequently abstracted to partial orders by Bourbaki in connection with Zorn's Lemma. Migrating beyond set theory, that generalization becomes cited as the strongest of fixed point theorems useful in computer science.
Section 1 describes the emergence of our guiding motif as a line of development from Cantor's diagonal proof to Russell's Paradox, fueled by the clarification of the inclusion vs. membership distinction. Section 2 engages the motif as fully participating in Zermelo's work on the Well-Ordering Theorem and as newly informing on Cantor's basic result that there is no bijection 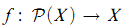 . Then Section 3 describes in connection with Zorn's Lemma the transformation of the motif into an abstract fixed point theorem, one accorded significance in computer science.
. Then Section 3 describes in connection with Zorn's Lemma the transformation of the motif into an abstract fixed point theorem, one accorded significance in computer science.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 20
- Cited by

