New Directions in Duality Theory for Modal Logic

Abstract

In this work we present some new contributions towards two different directions in the study of modal logic. First we employ tense logics to provide a temporal interpretation of intuitionistic quantifiers as “always in the future” and “sometime in the past.” This is achieved by modifying the Gödel translation and resolves an asymmetry between the standard interpretation of intuitionistic quantifiers.

Then we generalize the classic Gelfand–Naimark–Stone duality between compact Hausdorff spaces and uniformly complete bounded archimedean 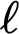$\ell $ -algebras to a duality encompassing compact Hausdorff spaces with continuous relations. This leads to the notion of modal operators on bounded archimedean 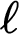$\ell $ -algebras and in particular on rings of continuous real-valued functions on compact Hausdorff spaces. This new duality is also a generalization of the classic Jónsson-Tarski duality in modal logic.

Abstract taken directly from the thesis.

E-mail: lcarai@unisa.it

URL: https://www.proquest.com/openview/5d284dbfb954383da9364149fa312b6f/1?pq-origsite=gscholar&cbl=18750&diss=y