Article contents
Two Applications of Inner Model Theory to the Study of 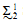 Sets
Sets
Published online by Cambridge University Press: 15 January 2014
Extract
§0. Preface. There has been an expectation that the endgame of the more tenacious problems raised by the Los Angeles ‘cabal’ school of descriptive set theory in the 1970's should ultimately be played out with the use of inner model theory. Questions phrased in the language of descriptive set theory, where both the conclusions and the assumptions are couched in terms that only mention simply definable sets of reals, and which have proved resistant to purely descriptive set theoretic arguments, may at last find their solution through the connection between determinacy and large cardinals.
Perhaps the most striking example was given by [24], where the core model theory was used to analyze the structure of HOD and then show that all regular cardinals below ΘL(ℝ) are measurable. John Steel's analysis also settled a number of structural questions regarding HOD L(ℝ), such as GCH.
Another illustration is provided by [21]. There an application of large cardinals and inner model theory is used to generalize the Harrington-Martin theorem that 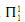 determinacy implies
determinacy implies 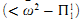 )determinacy.
)determinacy.
However, it is harder to find examples of theorems regarding the structure of the projective sets whose only known proof from determinacy assumptions uses the link between determinacy and large cardinals. We may equivalently ask whether there are second order statements of number theory that cannot be proved under PD–the axiom of projective determinacy–without appealing to the large cardinal consequences of the PD, such as the existence of certain kinds of inner models that contain given types of large cardinals.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 4
- Cited by

