No CrossRef data available.
Article contents
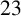 $23$-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION
$23$-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION
Part of:
Additive number theory; partitions
Published online by Cambridge University Press: 23 December 2022
Abstract
A partition of a positive integer n is called 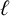 $\ell $-regular if none of its parts is divisible by
$\ell $-regular if none of its parts is divisible by 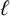 $\ell $. Denote by
$\ell $. Denote by 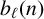 $b_{\ell }(n)$ the number of
$b_{\ell }(n)$ the number of 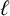 $\ell $-regular partitions of n. We give a complete characterisation of the arithmetic of
$\ell $-regular partitions of n. We give a complete characterisation of the arithmetic of 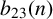 $b_{23}(n)$ modulo
$b_{23}(n)$ modulo 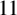 $11$ for all n not divisible by
$11$ for all n not divisible by 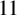 $11$ in terms of binary quadratic forms. Our result is obtained by establishing a relation between the generating function for these values of
$11$ in terms of binary quadratic forms. Our result is obtained by establishing a relation between the generating function for these values of 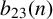 $b_{23}(n)$ and certain modular forms having complex multiplication by
$b_{23}(n)$ and certain modular forms having complex multiplication by 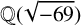 ${\mathbb Q}(\sqrt {-69})$.
${\mathbb Q}(\sqrt {-69})$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 254 - 263
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Ahlgren, S. and Lovejoy, J., ‘The arithmetic of partitions into distinct parts’, Mathematika 48(1–2) (2001), 203–211.10.1112/S0025579300014443CrossRefGoogle Scholar
Boll, E. and Penniston, D., ‘The
 $7$
-regular and
$7$
-regular and
 $13$
-regular partition functions modulo
$13$
-regular partition functions modulo
 $3$
’, Bull. Aust. Math. Soc. 93(3) (2016), 410–419.10.1017/S0004972715001434CrossRefGoogle Scholar
$3$
’, Bull. Aust. Math. Soc. 93(3) (2016), 410–419.10.1017/S0004972715001434CrossRefGoogle Scholar
Gordon, B. and Ono, K., ‘Divisibility of certain partition functions by powers of primes’, Ramanujan J. 1(1) (1997), 25–34.10.1023/A:1009711020492CrossRefGoogle Scholar
Ono, K. and Penniston, D., ‘The
 $2$
-adic behavior of the number of partitions into distinct parts’, J. Combin. Theory Ser. A 92(2) (2000), 138–157.10.1006/jcta.2000.3057CrossRefGoogle Scholar
$2$
-adic behavior of the number of partitions into distinct parts’, J. Combin. Theory Ser. A 92(2) (2000), 138–157.10.1006/jcta.2000.3057CrossRefGoogle Scholar
Penniston, D., ‘Arithmetic of
 $\ell$
-regular partition functions’, Int. J. Number Theory 4(2) (2008), 295–302.10.1142/S1793042108001341CrossRefGoogle Scholar
$\ell$
-regular partition functions’, Int. J. Number Theory 4(2) (2008), 295–302.10.1142/S1793042108001341CrossRefGoogle Scholar
Penniston, D., ‘
 $11$
-regular partitions and a Hecke eigenform’, Int. J. Number Theory 15(6) (2019), 1251–1259.10.1142/S1793042119500696CrossRefGoogle Scholar
$11$
-regular partitions and a Hecke eigenform’, Int. J. Number Theory 15(6) (2019), 1251–1259.10.1142/S1793042119500696CrossRefGoogle Scholar
Serre, J.-P., ‘Sur la lacunarité des puissances de
 $\eta$
’, Glasg. Math. J. 27 (1985), 203–221.10.1017/S0017089500006194CrossRefGoogle Scholar
$\eta$
’, Glasg. Math. J. 27 (1985), 203–221.10.1017/S0017089500006194CrossRefGoogle Scholar
Sturm, J., ‘On the congruence of modular forms’, in: Number Theory, Lecture Notes in Mathematics, 1240 (eds. Chudnovsky, D. V., Chudnovsky, G. V., Cohn, H. and Nathanson, M. B.) (Springer, Berlin–Heidelberg, 1984), 275–280.Google Scholar
Treneer, S., ‘Congruences for the coefficients of weakly holomorphic modular forms’, Proc. Lond. Math. Soc. (3) 93(2) (2006), 304–324.10.1112/S0024611506015814CrossRefGoogle Scholar
Webb, J. J., ‘Arithmetic of the
 $13$
-regular partition function modulo
$13$
-regular partition function modulo
 $3$
’, Ramanujan J. 25(1) (2011), 49–56.10.1007/s11139-010-9227-4CrossRefGoogle Scholar
$3$
’, Ramanujan J. 25(1) (2011), 49–56.10.1007/s11139-010-9227-4CrossRefGoogle Scholar


