Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-29T03:59:35.880Z Has data issue: false hasContentIssue false
  • English
  • Français

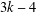THE $3k-4$ THEOREM FOR ORDERED GROUPS

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  28 September 2017

PREM PRAKASH PANDEY Open the ORCID record for PREM PRAKASH PANDEY [Opens in a new window]
PREM PRAKASH PANDEY*
Affiliation:
Department of Mathematics, IISER Berhampur, Government ITI Berhampur, Khodasingi, Berhampur-760010, India email premshivaganga@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, Freiman et al. [‘Small doubling in ordered groups’, J. Aust. Math. Soc. 96(3) (2014), 316–325] proved two ‘structure theorems’ for ordered groups. We give elementary proofs of these two theorems.

Keywords

3k - 4 theoremordered groups

MSC classification

Primary: 11P70: Inverse problems of additive number theory, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 43 - 46
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Freiman, G. A., Herzog, M., Longobardi, P. and Maj, M., ‘Small doubling in ordered groups’, J. Aust. Math. Soc. 96(3) (2014), 316–325.Google Scholar
Freiman, G. A., Herzog, M., Longobardi, P., Maj, M., Plagne, A., Robinson, D. J. S. and Stanchescu, Y. V., ‘On the structure of subsets of an orderable group, with some small doubling properties’, J. Algebra 445 (2016), 307–326.CrossRefGoogle Scholar
Freiman, G. A., Herzog, M., Longobardi, P., Maj, M., Plagne, A. and Stanchescu, Y. V., ‘Small doubling in ordered groups: generators and structures’, Groups Geom. Dyn. 11(2) (2017), 585–612.Google Scholar
Freiman, G. A., Herzog, M., Longobardi, P., Maj, M. and Stanchescu, Y. V., ‘Direct and inverse problems in additive number theory and in non-abelian group theory’, European J. Combin. 40 (2014), 42–54.Google Scholar
Freiman, G. A., Herzog, M., Longobardi, P., Maj, M. and Stanchescu, Y. V., ‘A small doubling structure theorem in a Baumslag–Solitar group’, European J. Combin. 44 (2015), 106–124.Google Scholar
Nathanson, M., Additive Number Theory: Inverse Problems and the Geometry of Sumsets, Graduate Texts in Mathematics, 165 (Springer, New York, 1996).CrossRefGoogle Scholar