Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T16:15:38.538Z Has data issue: false hasContentIssue false
  • English
  • Français

CENTRE OF BANACH ALGEBRA VALUED BEURLING ALGEBRAS

Part of: Methods of category theory in functional analysis Abstract harmonic analysis Locally compact groups and their algebras

Published online by Cambridge University Press:  13 September 2021

BHARAT TALWAR Open the ORCID record for BHARAT TALWAR [Opens in a new window]  and
RANJANA JAIN Open the ORCID record for RANJANA JAIN [Opens in a new window]
BHARAT TALWAR
Affiliation:
Department of Mathematics, University of Delhi, Delhi, India e-mail: btalwar.math@gmail.com
RANJANA JAIN*
Affiliation:
Department of Mathematics, University of Delhi, Delhi, India
*
e-mail: rjain@maths.du.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for a Banach algebra A having a bounded 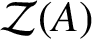$\mathcal {Z}(A)$ -approximate identity and for every $\mathbf {[IN]}$ group G with a weight w which is either constant on conjugacy classes or satisfies 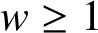$w \geq 1$ , 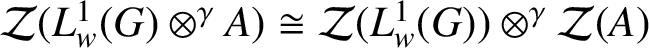$\mathcal {Z}(L^{1}_{w}(G) \otimes ^{\gamma } A) \cong \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A)$ . 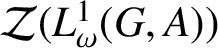As an application, we discuss the conditions under which $\mathcal {Z}(L^{1}_{\omega }(G,A))$ enjoys certain Banach algebraic properties, such as weak amenability or semisimplicity.

Keywords

vector-valued Beurling algebrasBanach space projective tensor productcentreweightweak amenability

MSC classification

Primary: 46M05: Tensor products
Secondary: 22D15: Group algebras of locally compact groups 43A20: $L^1$-algebras on groups, semigroups, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 3 , June 2022 , pp. 490 - 498
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Bharat Talwar is supported by a Senior Research Fellowship of CSIR (file number 09/045(1442)/ 2016-EMR-I).

References

Alaghmandan, M., Choi, Y. and Samei, E., ‘ZL-amenability and characters for the restricted direct products of finite groups’, J. Math. Anal. Appl. 411(1) (2014), 314–328.CrossRefGoogle Scholar
Azimifard, A., Samei, E. and Spronk, N., ‘Amenability properties of the centres of group algebras’, J. Funct. Anal. 256(5) (2009), 1544–1564.CrossRefGoogle Scholar
Dales, H. G., Banach Algebras and Automatic Continuity, London Mathematical Society Monographs, New Series, 24 (Oxford University Press, New York, 2000).Google Scholar
Dedania, H. V. and Kansagara, M. K., ‘Gelfand theory for vector-valued Beurling algebras’, Math. Today 29(2) (2013), 12–24.Google Scholar
Diestel, J. and Uhl, J. J. Jr., Vector Measures (American Mathematical Society, Providence, RI, 1977).CrossRefGoogle Scholar
Gelbaum, B. R., ‘Tensor products and related questions’, Trans. Amer. Math. Soc. 103 (1962), 525–548.CrossRefGoogle Scholar
Gupta, V. P. and Jain, R., ‘On Banach space projective tensor product of ${C}^{\ast }$ -algebras’, Banach J. Math. Anal. 14(2020), 524–538.CrossRefGoogle Scholar
Gupta, V. P., Jain, R. and Talwar, B., ‘On closed Lie ideals and center of generalized group algebras’, J. Math. Anal. Appl. 502(1) (2021), 125228.CrossRefGoogle Scholar
Kaniuth, E., A Course in Commutative Banach Algebras, Graduate Texts in Mathematics, 246 (Springer, New York, 2009).Google Scholar
Liukkonen, J. and Mosak, R., ‘Harmonic analysis and centers of group algebras’, Trans. Amer. Math. Soc. 195 (1974), 147–163.CrossRefGoogle Scholar
Liukkonen, J. and Mosak, R., ‘Harmonic analysis and centers of Beurling algebras’, Comment. Math. Helv. 52(3) (1977), 297–315.CrossRefGoogle Scholar
Mosak, R. D., ‘Central functions in group algebras’, Proc. Amer. Math. Soc. 29 (1971), 613–616.CrossRefGoogle Scholar
Mosak, R. D., ‘The ${L}^1$ - and ${C}^{\ast }$ -algebras of ${\left[\mathrm{FIA}\right]}_B^{-}$ groups, and their representations’, Trans. Amer. Math. Soc. 163 (1972), 277–310.Google Scholar
Reiter, H. and Stegeman, J. D., Classical Harmonic Analysis and Locally Compact Groups, 2nd edn, London Mathematical Society Monographs, New Series, 22 (Oxford University Press, New York, 2000).Google Scholar
Rickart, C. E., General Theory of Banach Algebras, The University Series in Higher Mathematics (D. van Nostrand, Princeton, NJ, 1960).Google Scholar
Ryan, R. A., Introduction to Tensor Products of Banach Spaces, Springer Monographs in Mathematics (Springer, London, 2002).CrossRefGoogle Scholar
Samei, E., ‘Weak amenability and 2-weak amenability of Beurling algebras’, J. Math. Anal. Appl. 346(2) (2008), 451–467.CrossRefGoogle Scholar
Shepelska, V. and Zhang, Y., ‘Weak amenability of the central Beurling algebras on ${\left[\mathrm{FC}\right]}^{-}$ groups’, Michigan Math. J. 66(2) (2017), 433–446.CrossRefGoogle Scholar
Tewari, U. B., Dutta, M. and Madan, S., ‘Tensor products of commutative Banach algebras’, Int. J. Math. Math. Sci. 5(3) (1982), 503–512.Google Scholar
Tomiyama, J., ‘Tensor products of commutative Banach algebras’, Tohoku Math. J. (2) 12 (1960), 147–154.CrossRefGoogle Scholar