No CrossRef data available.
Article contents
THE CHROMATIC NUMBER OF 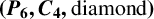 $\boldsymbol {(P_6,C_4,\mbox {diamond})}$-FREE GRAPHS
$\boldsymbol {(P_6,C_4,\mbox {diamond})}$-FREE GRAPHS
Part of:
Graph theory
Published online by Cambridge University Press: 03 October 2022
Abstract
The diamond is the complete graph on four vertices minus one edge; 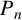 $P_n$ and
$P_n$ and 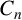 $C_n$ denote the path and cycle on n vertices, respectively. We prove that the chromatic number of a
$C_n$ denote the path and cycle on n vertices, respectively. We prove that the chromatic number of a 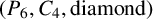 $(P_6,C_4,\mbox {diamond})$-free graph G is no larger than the maximum of 3 and the clique number of G.
$(P_6,C_4,\mbox {diamond})$-free graph G is no larger than the maximum of 3 and the clique number of G.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This research was partially supported by a grant from the National Natural Sciences Foundation of China (No. 11971111).
References
Bondy, J. and Murty, U. S. R., Graph Theory, Graduate Texts in Mathematics, 244 (Springer, Berlin, 2008).CrossRefGoogle Scholar
Cameron, K., Huang, S. and Merkel, O., ‘An optimal
 $\chi$
-bound for (
$\chi$
-bound for (
 ${P}_6$
, diamond)-free graphs’, J. Graph Theory 97 (2021), 451–465.CrossRefGoogle Scholar
${P}_6$
, diamond)-free graphs’, J. Graph Theory 97 (2021), 451–465.CrossRefGoogle Scholar
Char, A. and Karthick, T., ‘Coloring of (P5, 4-wheel)-free graphs’,
Discrete Math.
345 (2022), Article no 112795, 22 pages.CrossRefGoogle Scholar
Chudnovsky, M., Robertson, N., Seymour, P. and Thomas, R., ‘The strong perfect graph theorem’, Ann. of Math. (2) 164 (2006), 51–229.CrossRefGoogle Scholar
Chudnovsky, M. and Sivaraman, V., ‘Perfect divisibility and 2-divisibility’, J. Graph Theory 90 (2019), 54–60.CrossRefGoogle Scholar
Gaspers, S. and Huang, S., ‘Linearly
 $\chi$
-bounding
$\chi$
-bounding
 $\mathbf{\mathcal{H}}$
-free graphs’, J. Graph Theory 92 (2019), 322–342.CrossRefGoogle Scholar
$\mathbf{\mathcal{H}}$
-free graphs’, J. Graph Theory 92 (2019), 322–342.CrossRefGoogle Scholar
Goedgebeur, J., Huang, S., Ju, Y. and Merkel, O., ‘Colouring graphs with no induced six-vertex path or diamond’, Preprint, 2021, arXiv:2106.08602v1.CrossRefGoogle Scholar
Gravier, S., Hoàng, C. and Maffray, F., ‘Coloring the hypergraph of maximal cliques of a graph with no long path’, Discrete Math. 272 (2003), 285–290.CrossRefGoogle Scholar
Gyárfás, A., ‘Problems from the world surrounding perfect graphs’, Zastos. Mat. XIX (1987), 413–441.Google Scholar
Karthick, T. and Maffray, F., ‘Vizing bound for the chromatic number on some graph classes’, Graphs Combin. 32 (2016), 1447–1460.CrossRefGoogle Scholar
Karthick, T. and Maffray, F., ‘Square-free graphs with no six-vertex induced path’, SIAM J. Discrete Math. 33 (2019), 874–909.CrossRefGoogle Scholar
Karthick, T. and Mishra, S., ‘On the chromatic number of (
 ${P}_5$
, diamond)-free graphs’, Graphs Combin. 34 (2018), 677–692.CrossRefGoogle Scholar
${P}_5$
, diamond)-free graphs’, Graphs Combin. 34 (2018), 677–692.CrossRefGoogle Scholar
Kierstead, H., Penrice, S. and Trotter, W., ‘On-line and first-fit coloring of graphs that do not induce
 ${P}_5$
’, SIAM J. Discrete Math. 8 (1995), 485–498.CrossRefGoogle Scholar
${P}_5$
’, SIAM J. Discrete Math. 8 (1995), 485–498.CrossRefGoogle Scholar
Mycielski, J., ‘Sur le coloriage des graphes’, Colloq. Math. 3 (1955), 161–162.CrossRefGoogle Scholar
Schiermeyer, I., ‘Chromatic number of
 ${P}_5$
-free graphs: Reed’s conjecture’, Discrete Math. 343 (2016), 1940–1943.CrossRefGoogle Scholar
${P}_5$
-free graphs: Reed’s conjecture’, Discrete Math. 343 (2016), 1940–1943.CrossRefGoogle Scholar
Scott, A. and Seymour, P., ‘Induced subgraphs of graphs with large chromatic number. I. Odd holes’, J. Combin. Theory Ser. B 121 (2016), 68–84.CrossRefGoogle Scholar
Scott, A. and Seymour, P., ‘A survey of
 $\chi$
-boundedness’, J. Graph Theory 95 (2020), 473–504.CrossRefGoogle Scholar
$\chi$
-boundedness’, J. Graph Theory 95 (2020), 473–504.CrossRefGoogle Scholar
West, D., Introduction to Graph Theory, 2nd edn (Prentice-Hall, Englewood Cliffs, NJ, 2000).Google Scholar



