Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T14:12:30.201Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DIAMETER AND RADIUS OF RADIALLY MAXIMAL GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  11 January 2021

PU QIAO  and
XINGZHI ZHAN Open the ORCID record for XINGZHI ZHAN [Opens in a new window]
PU QIAO
Affiliation:
Department of Mathematics, East China University of Science and Technology, Shanghai200237, China e-mail: pq@ecust.edu.cn
XINGZHI ZHAN*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai200241, China
*
e-mail: zhan@math.ecnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A graph is called radially maximal if it is not complete and the addition of any new edge decreases its radius. Harary and Thomassen [‘Anticritical graphs’, Math. Proc. Cambridge Philos. Soc.79(1) (1976), 11–18] proved that the radius r and diameter d of any radially maximal graph satisfy $r\le d\le 2r-2.$ Dutton et al. [‘Changing and unchanging of the radius of a graph’, Linear Algebra Appl.217 (1995), 67–82] rediscovered this result with a different proof and conjectured that the converse is true, that is, if r and d are positive integers satisfying 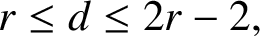$r\le d\le 2r-2,$ then there exists a radially maximal graph with radius r and diameter 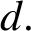$d.$ We prove this conjecture and a little more.

Keywords

diametereccentricityradially maximal graphradius

MSC classification

Primary: 05C12: Distance in graphs
Secondary: 05C35: Extremal problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 196 - 202
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by the NSFC grants 11671148 and 11771148 and the Science and Technology Commission of Shanghai Municipality (STCSM) grant 18dz2271000.

References

Dutton, R. D., Medidi, S. R. and Brigham, R. C., ‘Changing and unchanging of the radius of a graph’, Linear Algebra Appl. 217 (1995), 67–82.CrossRefGoogle Scholar
Gliviak, F., Knor, M. and Šoltés, L., ‘On radially maximal graphs’, Australas. J. Combin. 9 (1994), 275–284.Google Scholar
Harary, F. and Thomassen, C., ‘Anticritical graphs’, Math. Proc. Cambridge Philos. Soc. 79(1) (1976), 11–18.CrossRefGoogle Scholar
West, D. B., Introduction to Graph Theory (Prentice Hall, Upper Saddle River, NJ, 1996).Google Scholar