No CrossRef data available.
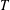 $T$-GAIN SPECTRA
$T$-GAIN SPECTRAPublished online by Cambridge University Press: 03 July 2020
An undirected graph 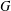 $G$ is determined by its
$G$ is determined by its 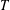 $T$-gain spectrum (DTS) if every
$T$-gain spectrum (DTS) if every 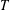 $T$-gain graph cospectral to
$T$-gain graph cospectral to 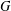 $G$ is switching equivalent to
$G$ is switching equivalent to 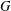 $G$. We show that the complete graph
$G$. We show that the complete graph 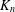 $K_{n}$ and the graph
$K_{n}$ and the graph  $K_{n}-e$ obtained by deleting an edge from
$K_{n}-e$ obtained by deleting an edge from 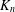 $K_{n}$ are DTS, the star
$K_{n}$ are DTS, the star 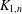 $K_{1,n}$ is DTS if and only if
$K_{1,n}$ is DTS if and only if 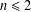 $n\leq 2$, and an odd path
$n\leq 2$, and an odd path 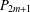 $P_{2m+1}$ is not DTS if
$P_{2m+1}$ is not DTS if 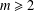 $m\geq 2$. We give an operation for constructing cospectral
$m\geq 2$. We give an operation for constructing cospectral 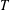 $T$-gain graphs and apply it to show that a tree of arbitrary order (at least
$T$-gain graphs and apply it to show that a tree of arbitrary order (at least 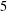 $5$) is not DTS.
$5$) is not DTS.
The first author is supported by the National Natural Science Foundation of China (No.11971474). The third author is supported by the Natural Science Foundation of Shandong Province (No. ZR2019BA016).