Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-26T15:07:50.088Z Has data issue: false hasContentIssue false
  • English
  • Français

MAX-CUT BY EXCLUDING BIPARTITE SUBGRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  08 November 2022

SHUFEI WU Open the ORCID record for SHUFEI WU [Opens in a new window]  and
AMIN LI Open the ORCID record for AMIN LI [Opens in a new window]
SHUFEI WU*
Affiliation:
School of Mathematics and Information Science, Henan Polytechnic University, Henan 454003, PR China
AMIN LI
Affiliation:
School of Mathematics and Information Science, Henan Polytechnic University, Henan 454003, PR China e-mail: liamin929@126.com
*
e-mail: shufeiwu@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For a graph G, let 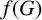$f(G)$ denote the maximum number of edges in a bipartite subgraph of G. Given a positive integer m and a fixed graph H, let 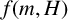$f(m,H)$ denote the minimum possible cardinality of 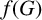$f(G)$, as G ranges over all graphs on m edges that contain no copy of H. We prove bounds on 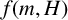$f(m,H)$ for some bipartite graphs H and give a bound for a conjecture of Alon et al. [‘MaxCut in H-free graphs’, Combin. Probab. Comput. 14 (2005), 629–647] concerning 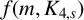$f(m,K_{4,s})$.

Keywords

H-free graphmax-cutbipartite subgraph

MSC classification

Primary: 05C70: Factorization, matching, partitioning, covering and packing
Secondary: 05C35: Extremal problems 05C75: Structural characterization of families of graphs
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 177 - 186
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by the National Natural Science Foundation of China (No. 11801149).

References

Alon, N., ‘Bipartite subgraphs’, Combinatorica 16 (1996), 301–311.10.1007/BF01261315CrossRefGoogle Scholar
Alon, N., Bollobás, B., Krivelevich, M. and Sudakov, B., ‘Maximum cuts and judicious partitions in graphs without short cycles’, J. Combin. Theory Ser. B 88 (2003), 329–346.10.1016/S0095-8956(03)00036-4CrossRefGoogle Scholar
Alon, N., Krivelevich, M. and Sudakov, B., ‘Turán numbers of bipartite graphs and related Ramsey-type questions’, Combin. Probab. Comput. 12 (2003), 477–494.10.1017/S0963548303005741CrossRefGoogle Scholar
Alon, N., Krivelevich, M. and Sudakov, B., ‘MaxCut in $H$ -free graphs’, Combin. Probab. Comput. 14 (2005), 629–647.10.1017/S0963548305007017CrossRefGoogle Scholar
Alon, N., Rónyai, L. and Szabó, T., ‘Norm-graphs: variations and applications’, J. Combin. Theory Ser. B 76 (1999), 280–290.10.1006/jctb.1999.1906CrossRefGoogle Scholar
Carlson, C., Kolla, A., Li, R., Mani, N., Sudakov, B. and Trevisan, L., ‘Lower bounds for Max-Cut in $H$ -free graphs via semidefinite programming’, SIAM J. Discrete Math. 35 (2021), 1557–1568.10.1137/20M1333985CrossRefGoogle Scholar
Edwards, C. S., ‘Some extremal properties of bipartite subgraphs’, Canad. J. Math. 25 (1973), 475–485.10.4153/CJM-1973-048-xCrossRefGoogle Scholar
Edwards, C. S., ‘An improved lower bound for the number of edges in a largest bipartite subgraph’, in: Recent Advances in Graph Theory: Proceedings of 2nd Czechoslovak Symposium on Graph Theory, Prague, 1974 (ed. Fiedler, M.) (Academia, Praha, 1975), 167–181.Google Scholar
Erdős, P., ‘On even subgraphs of graphs’, Mat. Lapok (N.S.) 18 (1967), 283–288.Google Scholar
Erdős, P., ‘Problems and results in graph theory and combinatorial analysis’, in: Graph Theory and Related Topics (eds. Bondy, J. A., Murty, U. S. R. and Tutte, W. T.) (Academic Press, New York–London, 1979), 153–163.Google Scholar
Erdős, P., Gyárfás, A. and Kohayakawa, Y., ‘The size of the largest bipartite subgraphs’, Discrete Math. 177 (1997), 267–271.10.1016/S0012-365X(97)00004-6CrossRefGoogle Scholar
Erdős, P. and Simonovits, M., ‘Some extremal problems in graph theory’, in: Combinatorial Theory and Its Applications 1, Colloquia Mathematica Societatis János Bolyai, 4 (eds. Erdős, P., Rényi, A. and Sós, V. T.) (North-Holland, Amsterdam, 1970), 377–390.Google Scholar
Faudree, R. J. and Simonovits, M., ‘On a class of degenerate extremal graph problems’, Combinatorica 3 (1983), 83–93.10.1007/BF02579343CrossRefGoogle Scholar
Füredi, Z., ‘On a Turán type problem of Erdős’, Combinatorica 11 (1991), 75–79.10.1007/BF01375476CrossRefGoogle Scholar
Glock, S., Janzer, O. and Sudakov, B., ‘New results for MaxCut in $H$ -free graphs’, Preprint, 2021, arXiv:2104.06971.Google Scholar
Hou, J. and Wu, S., ‘On bisections of graphs without complete bipartite graphs’, J. Graph Theory 98 (2021), 630–641.10.1002/jgt.22717CrossRefGoogle Scholar
Karp, R. M., ‘Reducibility among combinatorial problems’, in: Complexity of Computer Computations (eds. Miller, R. E., Thatcher, J. W. and Bohlinger, J. D.) (Plenum Press, New York, 1972), 85–103.10.1007/978-1-4684-2001-2_9CrossRefGoogle Scholar
Kővári, P., Sós, V. T. and Turán, P., ‘On a problem of Zarankiewicz’, Colloq. Math. 3 (1954), 50–57.10.4064/cm-3-1-50-57CrossRefGoogle Scholar
Lin, J., ‘Maximum bipartite subgraphs in $H$ -free graphs’, Czechoslovak Math. J. 72 (2022), 621–635.10.21136/CMJ.2022.0302-20CrossRefGoogle Scholar
Lin, J., Zeng, Q. and Chen, F., ‘Maximum cuts in graphs without wheels’, Bull. Aust. Math. Soc. 100 (2019), 13–26.10.1017/S0004972718001259CrossRefGoogle Scholar
Shearer, J. B., ‘A note on bipartite subgraphs of triangle-free graphs’, Random Structures Algorithms 3 (1992), 223–226.10.1002/rsa.3240030211CrossRefGoogle Scholar
Zeng, Q. and Hou, J., ‘Bipartite subgraphs of $H$ -free graphs’, Bull. Aust. Math. Soc. 96 (2017), 1–13.10.1017/S0004972716001295CrossRefGoogle Scholar
Zeng, Q. and Hou, J., ‘Maximum cuts of graphs with forbidden cycles’, Ars Math. Contemp. 15 (2018), 147–160.10.26493/1855-3974.1218.5edCrossRefGoogle Scholar