Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-26T15:21:32.293Z Has data issue: false hasContentIssue false
  • English
  • Français

MONOMIAL AND MONOLITHIC CHARACTERS OF FINITE SOLVABLE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  05 October 2021

BURCU ÇINARCI Open the ORCID record for BURCU ÇINARCI [Opens in a new window]
BURCU ÇINARCI*
Affiliation:
Maritime Faculty, Department of Marine Engineering, Piri Reis University, Istanbul 34940, Turkey
*
e-mail: burcu-cinarci@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite solvable group and let p be a prime divisor of 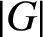$|G|$ . We prove that if every monomial monolithic character degree of G is divisible by p, then G has a normal p-complement and, if p is relatively prime to every monomial monolithic character degree of G, then G has a normal Sylow p-subgroup. We also classify all finite solvable groups having a unique imprimitive monolithic character.

Keywords

solvable groupmonolithic charactermonomial characterprimitive character

MSC classification

Primary: 20C15: Ordinary representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 3 , June 2022 , pp. 440 - 448
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work of the author was supported by the Scientific Research Projects Coordination Unit of Piri Reis University (project number BAP-2020-004).

References

Berkovich, Y. G., ‘On Isaacs’ three character degrees theorem’, Proc. Amer. Math. Soc. 125(3) (1997), 669–677.CrossRefGoogle Scholar
Berkovich, Y. G. and Zhmud, E. M., Characters of Finite Groups. Part 2, Translations of Mathematical Monographs, 101 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Djoković, D. Z. and Malzan, J., ‘Monomial irreducible characters of the symmetric and alternating groups’, J. Algebra 35 (1975), 153–158.Google Scholar
Erkoç, T. and Çınarcı, B., ‘Monolithic characters of real groups’, Comm. Algebra 49(8) (2021), 3192–3199.CrossRefGoogle Scholar
Erkoç, T. and Çınarcı, B., ‘Finite solvable groups with few imprimitive irreducible characters,’ J. Algebra Appl., to appear. doi:10.1142/S0219498822500669.CrossRefGoogle Scholar
Gallagher, P. X., ‘Group characters and normal Hall subgroups’, Nagoya Math. J. 21 (1962), 223–230.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin, 1967).CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups, London Mathematical Society Lecture Note Series, 185 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Pang, L. and Lu, J., ‘Finite groups and degrees of irreducible monomial characters’, J. Algebra Appl. 15(4) (2016), Article no. 1650073.CrossRefGoogle Scholar
Revin, D. O. and Vdovin, E. P., ‘Frattini argument for Hall subgroups’, J. Algebra 414 (2014), 95–104.CrossRefGoogle Scholar
Seitz, G. M., ‘Finite groups having only one irreducible representation of degree greater than one’, Proc. Amer. Math. Soc. 19 (1968), 459–461.CrossRefGoogle Scholar