Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-26T15:09:58.719Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON OPEN BOOK EMBEDDINGS OF 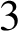$3$-MANIFOLDS IN 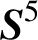$\boldsymbol {S}^5$

Part of: Differential topology

Published online by Cambridge University Press:  04 October 2021

SUHAS PANDIT Open the ORCID record for SUHAS PANDIT [Opens in a new window]  and
SELVAKUMAR A Open the ORCID record for SELVAKUMAR A [Opens in a new window]
SUHAS PANDIT
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, IIT PO, Chennai 600 036, Tamil Nadu, India e-mail: suhas@iitm.ac.in
SELVAKUMAR A*
Affiliation:
The Institute of Mathematical Sciences, Chennai, IV Cross Road, CIT Campus, Taramani, Chennai 600 113, Tamil Nadu, India
*
e-mail: aselvammaths@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we show that given a closed connected oriented 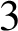$3$ -manifold M, there exists a knot K in M such that the manifold 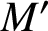$M'$ obtained from M by performing an integer surgery admits an open book decomposition which embeds into the trivial open book of the 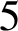$5$ -sphere 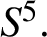$S^5.$

Keywords

open bookembedding

MSC classification

Primary: 57R40: Embeddings
Secondary: 57R15: Specialized structures on manifolds (spin manifolds, framed manifolds, etc.) 57R65: Surgery and handlebodies
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 3 , June 2022 , pp. 499 - 506
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, J., ‘A lemma on systems of knotted curves’, Proc. Natl. Acad. Sci. USA 9 (1923), 93–95.CrossRefGoogle ScholarPubMed
Etnyre, J., ‘Lectures on open book decompositions and contact structures’, in: Floer Homology, Gauge Theory, and Low Dimensional Topology, Clay Mathematics Proceedings, 5 (American Mathematical Society, Providence, RI, 2006), 103–141.Google Scholar
Ghanwat, A., Pandit, S. and A, Selvakumar, ‘Open book embeddings of closed non-orientable $3$ -manifolds’, Rocky Mountain J. Math. 49(4) (2019), 1143–1168.CrossRefGoogle Scholar
Giroux, E., ‘Géométrie de contact: de la dimension trois vers les dimensions supérieures’, Proc. ICM, Beijing, 2 (Higher Ed. Press, Beijing, 2002), 405–414.Google Scholar
Hirose, S. and Yasuhara, A., ‘Surfaces in $4$ -manifolds and their mapping class groups’, Topology 47 (2008), 41–50.CrossRefGoogle Scholar
Humphries, S., ‘Generators for the mapping class group’, in: Topology of Low Dimensional Manifolds, Lecture Notes in Mathematics, 722 (ed. Fenn, R.) (Springer, Berlin, 1979), 44–47.CrossRefGoogle Scholar
Johnson, D., ‘The structure of the Torelli group I: a finite set of generators for $\mathcal{J}$ ’, Ann. of Math. (2) 118 (1983), 423–442.CrossRefGoogle Scholar
Myers, R., ‘Open book decompositions of $3$ -manifolds’, Proc. Amer. Math. Soc. 72(2) (1978), 397–402.CrossRefGoogle Scholar
Pancholi, D., Pandit, S. and Saha, K., ‘Embeddings of $3$ -manifolds via open books’, Preprint, 2018.Google Scholar
Pandit, S. and A, Selvakumar, ‘Embeddings of $4$ -manifolds in ${S}^4\ {\tilde{\times}}\ {S}^2$ ’, Preprint.Google Scholar
Thurston, W. and Winkelnkemper, H., ‘On the existence of contact forms’, Proc. Amer. Math. Soc. 52 (1975), 345–347.CrossRefGoogle Scholar