Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T13:02:46.458Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE SINGULARITY OF ORIENTED GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  25 April 2022

XIAOBIN MA Open the ORCID record for XIAOBIN MA [Opens in a new window]  and
FAN JIANG Open the ORCID record for FAN JIANG [Opens in a new window]
XIAOBIN MA*
Affiliation:
School of Mathematics and Big Data, Anhui University of Science and Technology, Huainan, PR China
FAN JIANG
Affiliation:
School of Mathematics and Big Data, Anhui University of Science and Technology, Huainan, PR China e-mail: 1686951558@qq.com
*
e-mail: maxiaobinzaozhuang@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

An oriented graph is called singular or nonsingular according as its adjacency matrix is singular or nonsingular. In this note, by a new approach, we determine the singularity of oriented quasi-trees. The main results of Chen et al. [‘Singularity of oriented graphs from several classes’, Bull. Aust. Math. Soc. 102(1) (2020), 7–14] follow as corollaries. Furthermore, we give a necessary condition for an oriented bipartite graph to be nonsingular. By applying this condition, we characterise nonsingular oriented bipartite graphs 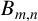$B_{m,n}$ when 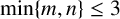$\min \{m,n\}\leq 3$ .

Keywords

singularityoriented graphadjacency matrix

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 357 - 362
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by National Natural Science Foundation of China (12001010), Natural Science Foundation of Anhui Province (1908085QA31), China Postdoctoral Foundation (2019M662131).

References

Chen, X., Yang, J., Geng, X. and Wang, L., ‘Singularity of oriented graphs from several classes’, Bull. Aust. Math. Soc. 102(1) (2020), 7–14.CrossRefGoogle Scholar
Cheng, B. and Liu, B., ‘On the nullity of tricyclic graphs’, Linear Algebra Appl. 434 (2011), 1799–1810.CrossRefGoogle Scholar
Collatz, L. and Sinogowitz, U., ‘Spektren endlicher Grafen’, Abh. Math. Semin. Univ. Hambg. 21 (1957), 63–77.CrossRefGoogle Scholar
Cvetković, D., Doob, M. and Sachs, H., Spectra of Graphs: Theory and Application (Academic Press, New York, 1980).Google Scholar
Cvetković, D. and Gutman, I., ‘The algebraic multiplicity of the number zero in the spectrum of a bipartite graph’, Mat. Vesnik, Beograd 9 (1972), 141–150.Google Scholar
Cvetković, D., Gutman, I. and Trinajstíc, N., ‘Graph theory and molecular orbitals II’, Croat. Chem. Acta 44 (1972), 365–374.Google Scholar
Fan, Y. and Qian, K., ‘On the nullity of bipartite graphs’, Linear Algebra Appl. 430 (2009), 2943–2949.CrossRefGoogle Scholar
Guo, J., Yan, W. and Yeh, Y.-N., ‘On the nullity and the matching number of unicyclic graphs’, Linear Algebra Appl. 431 (2009), 1293–1301.CrossRefGoogle Scholar
Gutman, I. and Sciriha, I., ‘On the nullity of line graphs of trees’, Discrete Math. 232 (2001), 35–45.CrossRefGoogle Scholar
Hu, S., Tan, X. and Liu, B., ‘On the nullity of bicyclic graphs’, Linear Algebra Appl. 429 (2008), 1387–1391.CrossRefGoogle Scholar
Hückel, E., ‘Quantentheoretische Beiträge zum Benzolproblem’, Z. Phys. 70 (1931), 204–286.CrossRefGoogle Scholar
Li, H., Fan, Y. and Su, L., ‘On the nullity of the line graph of unicyclic graph with depth one’, Linear Algebra Appl. 437 (2012), 2038–2055.CrossRefGoogle Scholar
Monsalve, J. and Rada, J., ‘Oriented bipartite graphs with minimal trace norm’, Linear Multilinear Algebra 67(6) (2019), 1121–1131.CrossRefGoogle Scholar
Zhang, Y., Xu, F. and Wong, D., ‘Characterization of oriented graphs of rank 2’, Linear Algebra Appl. 579 (2019), 136–147.CrossRefGoogle Scholar