No CrossRef data available.
Published online by Cambridge University Press: 22 October 2019
Let 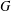 $G$ be a finite group with two primitive permutation representations on the sets
$G$ be a finite group with two primitive permutation representations on the sets 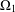 $\unicode[STIX]{x1D6FA}_{1}$ and
$\unicode[STIX]{x1D6FA}_{1}$ and 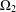 $\unicode[STIX]{x1D6FA}_{2}$ and let
$\unicode[STIX]{x1D6FA}_{2}$ and let 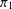 $\unicode[STIX]{x1D70B}_{1}$ and
$\unicode[STIX]{x1D70B}_{1}$ and 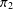 $\unicode[STIX]{x1D70B}_{2}$ be the corresponding permutation characters. We consider the case in which the set of fixed-point-free elements of
$\unicode[STIX]{x1D70B}_{2}$ be the corresponding permutation characters. We consider the case in which the set of fixed-point-free elements of 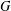 $G$ on
$G$ on 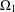 $\unicode[STIX]{x1D6FA}_{1}$ coincides with the set of fixed-point-free elements of
$\unicode[STIX]{x1D6FA}_{1}$ coincides with the set of fixed-point-free elements of 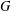 $G$ on
$G$ on 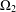 $\unicode[STIX]{x1D6FA}_{2}$, that is, for every
$\unicode[STIX]{x1D6FA}_{2}$, that is, for every 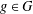 $g\in G$,
$g\in G$, 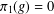 $\unicode[STIX]{x1D70B}_{1}(g)=0$ if and only if
$\unicode[STIX]{x1D70B}_{1}(g)=0$ if and only if 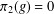 $\unicode[STIX]{x1D70B}_{2}(g)=0$. We have conjectured in Spiga [‘Permutation characters and fixed-point-free elements in permutation groups’, J. Algebra299(1) (2006), 1–7] that under this hypothesis either
$\unicode[STIX]{x1D70B}_{2}(g)=0$. We have conjectured in Spiga [‘Permutation characters and fixed-point-free elements in permutation groups’, J. Algebra299(1) (2006), 1–7] that under this hypothesis either 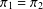 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}_{2}$ or one of
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}_{2}$ or one of  $\unicode[STIX]{x1D70B}_{1}-\unicode[STIX]{x1D70B}_{2}$ and
$\unicode[STIX]{x1D70B}_{1}-\unicode[STIX]{x1D70B}_{2}$ and 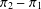 $\unicode[STIX]{x1D70B}_{2}-\unicode[STIX]{x1D70B}_{1}$ is a genuine character. In this paper we give evidence towards the veracity of this conjecture when the socle of
$\unicode[STIX]{x1D70B}_{2}-\unicode[STIX]{x1D70B}_{1}$ is a genuine character. In this paper we give evidence towards the veracity of this conjecture when the socle of 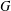 $G$ is a sporadic simple group or an alternating group. In particular, the conjecture is reduced to the case of almost simple groups of Lie type.
$G$ is a sporadic simple group or an alternating group. In particular, the conjecture is reduced to the case of almost simple groups of Lie type.